SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. OM77
Measuring Historical Volatility
- 23 июня 2014, 16:20
- |
Вычисление подразумеваемой (implied) волатильности – задача хоть и не тривиальная (требуется знание численных методов), но весьма простая. К тому же мы всегда имеем уникальное единственное решение – значение волатильности для заданного опциона. С исторической (historical) волатильноcтью дела обстоят несколько сложнее. Количество наблюдений, участвующих в расчетах, и метод ee оценки оказывают сильное влияние на конечный результат.
За основу данного поста взят материал из моей статьи в Financial One.
Рассмотрим основные методы оценки исторической волатильности и разберем их особенности.
В срочной секции Московской Биржи активно торгуются фьючерсы на обменный курс доллара США к рублю и опционы на этот контракт. В последнее время волатильность данного фьючерсного контракта возросла. Оценим его историческую волатильность.
Так как срочный контракт имеет ограниченный срок обращения, заменим его спотовым активом – валютной парой USD/RUB. Корреляция этих активов крайне высока. Для учета разницы во времени торгов будем использовать внутридневные цены только из временного интервала, соответствующего дневной торговой сессии на срочном рынке Московской биржи – с 10:00 до 18:45. Для этих данных вычислим дневные цены: open (O), high (H), low (L), close (C ) – и будем использовать полученные данные для расчета исторической волатильности.
Оценку волатильности будем производить по 22 торговым дням (примерно 1 месяц) следующими методами: Close-to-close, Parkinson, Garman-Klass, Rogers-Satchell, Garman-KlassYang-Zhang extension, Yang-Zhang.
1. Close-to-close (C )
Наиболее часто употребляемый метод для оценки исторической волатильности. В расчетах используются только цены закрытия (close). Формулы и подробное описание смотрите на моем сайте quant-lab.com
2. Parkinson (HL)
При оценке данным методом используются максимальные (high) и минимальные (low) цены торговой сессии. Данный метод не учитывает jumps (прыжки – разрыв в ценах закрытия и открытия между сессиями). Также метод не учитывает drift (направленное движение, тренд). В среднем это метод недооценивает волатильность, но тем не менее он эффективней предыдущего метода (см. Таблицу 1).
3. Garman-Klass (OHLC)
Оценка наиболее эффективна для активов с динамикой броуновского движения, с нулевым дрифтом и без прыжков. Хотя данный метод эффективнее двух предыдущих, тем не менее, он как правило недооценивает уровень волатильности.
4. Rogers-Satchell (OHLC)
Эффективность данного метода соизмерима с методом Garman-Klass. Однако это метод учитывает дрифт, но недостаточно хорошо «справляется» с прыжками, что приводит к недооценке волатильности.
5. Garman-Klass Yang-Zhang extension (OHLC)
Этот метод позволяет учитывать разрывы в ценах между открытием торговой сессии и закрытием предыдущей (jumps), но подразумевает нулевой дрифт.
6. Yang-Zhang (OHLC)
Наиболее мощный метод для оценки исторической волатильности, имеющий минимальный уровень ошибки. Оценка равна взвешенному среднему оценки Rogers-Satchell, close-open волатильности и open-close волатильности.
Результаты сравнения методов по признакам: какие данные используются, учитываются ли drift и jumps, а также эффективность каждого метода согласно [1] приводятся в Таблице 1.
Таблица 1. Сравнение методов

Динамика обменного курса USD/RUB и значения волатильности, рассчитанные указанными выше методами изображены на Рисунке 1. Период: 2013-01-08 – 2014-06-13.
Рисунок 1. Динамика обменного курса USDRUB и исторические волатильности
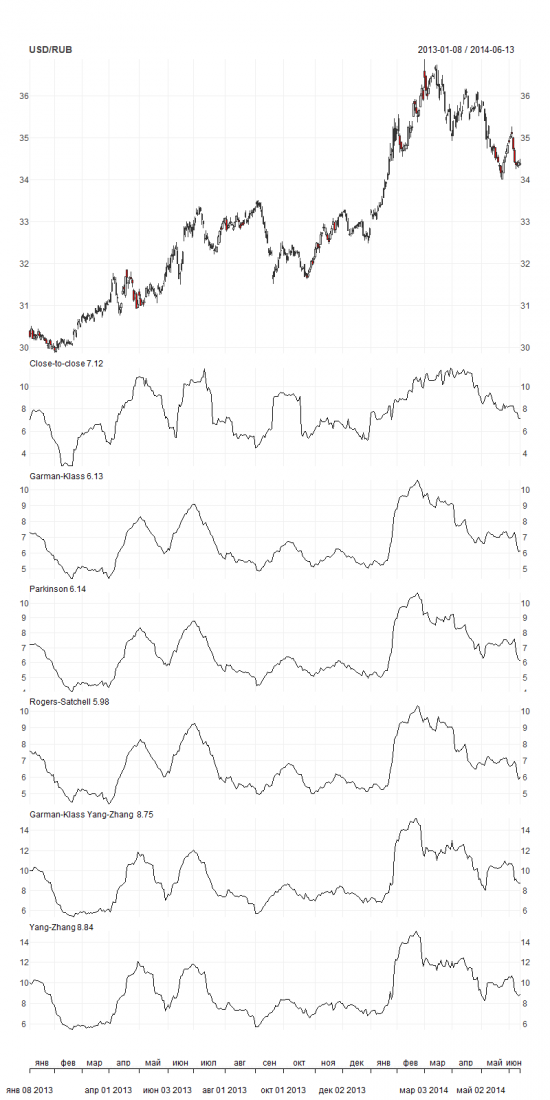
Максимальное текущее значение волатильности показывает метод Yang-Zhang, имеющий максимальный рейтинг согласно Таблице 1. Стоит отметить, что это не случайно, т.к. остальные методы склонны занижать оценку волатильности.
Интересно, что динамика волатильности на двух нижних графиках не согласуется с динамикой на остальных графиках, на которых волатильность обновила локальный минимум. Вероятная причина этого – наличие прыжков, наблюдаемых в последнее время на рынке. Принимая это во внимание, а также тот факт, что подразумеваемая волатильность сейчас находится на своих локальных минимумах, можно сделать предположение, что рынок недооценивает волатильность USD/RUB.
На Рисунках 2 – 7 представлена динамика исторической волатильности, рассчитанной различными методами, в сравнении с ее средними значениями за месяц, квартал, полгода и год.
Рисунок 2. Историческая волатильность Close-to-Close
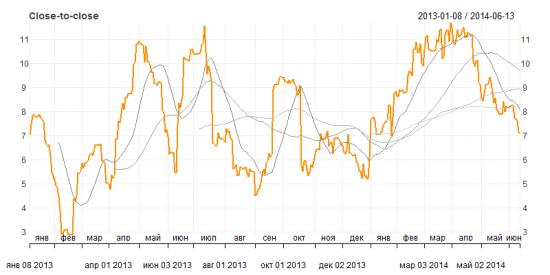
Рисунок 3. Историческая волатильность Garman-Klass
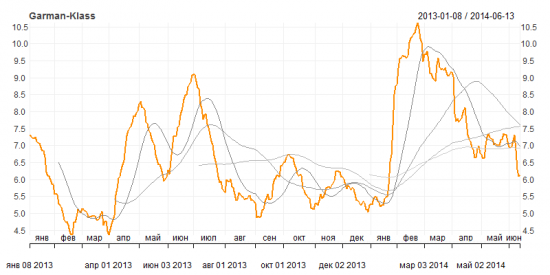
Рисунок 4. Историческая волатильность Parkinson
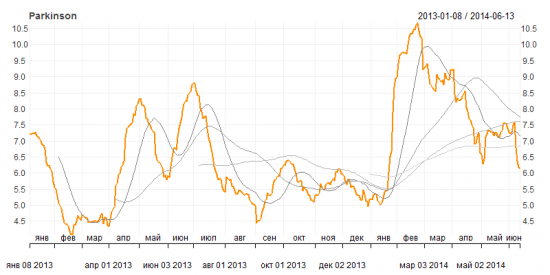
Рисунок 5. Историческая волатильность Rogers-Satchell
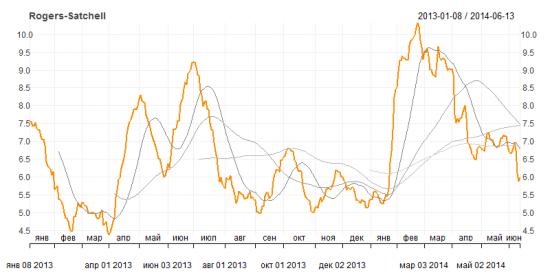
Рисунок 6. Историческая волатильность Garman-Klass Yang-Zhang extension
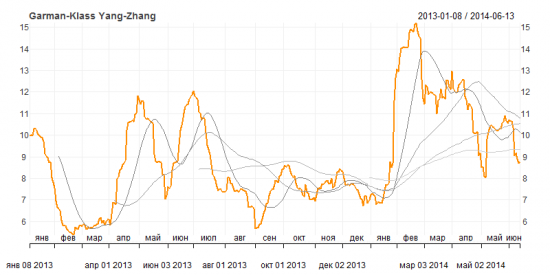
Рисунок 7. Историческая волатильность Yang-Zhang
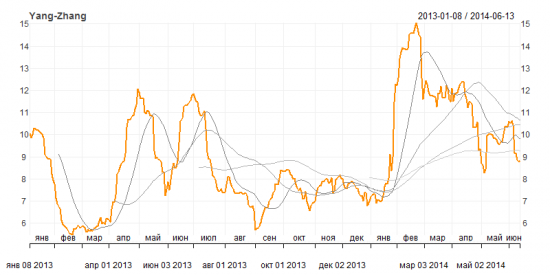
Согласно этим графикам волатильность снижается и находится сейчас ниже своего среднего годового значения, имеющего нейтральную динамику последние два месяца. Среднемесячная волатильность тем не менее находится выше среднего значения волатильности за год, но ниже квартального и полугодового. Тот факт, что волатильность, не встречая сопротивления, снизилась ниже своих полугодовых и годовых средних значений, придает уверенности, что нисходящий тренд в динамике волатильности достаточно сильный, и это движение вероятно продолжится.
За основу данного поста взят материал из моей статьи в Financial One.
Рассмотрим основные методы оценки исторической волатильности и разберем их особенности.
В срочной секции Московской Биржи активно торгуются фьючерсы на обменный курс доллара США к рублю и опционы на этот контракт. В последнее время волатильность данного фьючерсного контракта возросла. Оценим его историческую волатильность.
Так как срочный контракт имеет ограниченный срок обращения, заменим его спотовым активом – валютной парой USD/RUB. Корреляция этих активов крайне высока. Для учета разницы во времени торгов будем использовать внутридневные цены только из временного интервала, соответствующего дневной торговой сессии на срочном рынке Московской биржи – с 10:00 до 18:45. Для этих данных вычислим дневные цены: open (O), high (H), low (L), close (C ) – и будем использовать полученные данные для расчета исторической волатильности.
Оценку волатильности будем производить по 22 торговым дням (примерно 1 месяц) следующими методами: Close-to-close, Parkinson, Garman-Klass, Rogers-Satchell, Garman-KlassYang-Zhang extension, Yang-Zhang.
1. Close-to-close (C )
Наиболее часто употребляемый метод для оценки исторической волатильности. В расчетах используются только цены закрытия (close). Формулы и подробное описание смотрите на моем сайте quant-lab.com
2. Parkinson (HL)
При оценке данным методом используются максимальные (high) и минимальные (low) цены торговой сессии. Данный метод не учитывает jumps (прыжки – разрыв в ценах закрытия и открытия между сессиями). Также метод не учитывает drift (направленное движение, тренд). В среднем это метод недооценивает волатильность, но тем не менее он эффективней предыдущего метода (см. Таблицу 1).
3. Garman-Klass (OHLC)
Оценка наиболее эффективна для активов с динамикой броуновского движения, с нулевым дрифтом и без прыжков. Хотя данный метод эффективнее двух предыдущих, тем не менее, он как правило недооценивает уровень волатильности.
4. Rogers-Satchell (OHLC)
Эффективность данного метода соизмерима с методом Garman-Klass. Однако это метод учитывает дрифт, но недостаточно хорошо «справляется» с прыжками, что приводит к недооценке волатильности.
5. Garman-Klass Yang-Zhang extension (OHLC)
Этот метод позволяет учитывать разрывы в ценах между открытием торговой сессии и закрытием предыдущей (jumps), но подразумевает нулевой дрифт.
6. Yang-Zhang (OHLC)
Наиболее мощный метод для оценки исторической волатильности, имеющий минимальный уровень ошибки. Оценка равна взвешенному среднему оценки Rogers-Satchell, close-open волатильности и open-close волатильности.
Результаты сравнения методов по признакам: какие данные используются, учитываются ли drift и jumps, а также эффективность каждого метода согласно [1] приводятся в Таблице 1.
Таблица 1. Сравнение методов

Динамика обменного курса USD/RUB и значения волатильности, рассчитанные указанными выше методами изображены на Рисунке 1. Период: 2013-01-08 – 2014-06-13.
Рисунок 1. Динамика обменного курса USDRUB и исторические волатильности

Максимальное текущее значение волатильности показывает метод Yang-Zhang, имеющий максимальный рейтинг согласно Таблице 1. Стоит отметить, что это не случайно, т.к. остальные методы склонны занижать оценку волатильности.
Интересно, что динамика волатильности на двух нижних графиках не согласуется с динамикой на остальных графиках, на которых волатильность обновила локальный минимум. Вероятная причина этого – наличие прыжков, наблюдаемых в последнее время на рынке. Принимая это во внимание, а также тот факт, что подразумеваемая волатильность сейчас находится на своих локальных минимумах, можно сделать предположение, что рынок недооценивает волатильность USD/RUB.
На Рисунках 2 – 7 представлена динамика исторической волатильности, рассчитанной различными методами, в сравнении с ее средними значениями за месяц, квартал, полгода и год.
Рисунок 2. Историческая волатильность Close-to-Close

Рисунок 3. Историческая волатильность Garman-Klass

Рисунок 4. Историческая волатильность Parkinson

Рисунок 5. Историческая волатильность Rogers-Satchell

Рисунок 6. Историческая волатильность Garman-Klass Yang-Zhang extension

Рисунок 7. Историческая волатильность Yang-Zhang

Согласно этим графикам волатильность снижается и находится сейчас ниже своего среднего годового значения, имеющего нейтральную динамику последние два месяца. Среднемесячная волатильность тем не менее находится выше среднего значения волатильности за год, но ниже квартального и полугодового. Тот факт, что волатильность, не встречая сопротивления, снизилась ниже своих полугодовых и годовых средних значений, придает уверенности, что нисходящий тренд в динамике волатильности достаточно сильный, и это движение вероятно продолжится.
1.5К |
Читайте на SMART-LAB:

Календарь первички ВДО и розничных облигаций (СЗА доходность 28,71% | РДВ Технолоджи доходность 26,92% | ТЛК доходность 26,83%)
🔸 ПКО СЗА БО-06 (для квал. инвесторов, BB–|ru| , 200 млн руб., ставки купона 25,25%, YTM 28,39%, дюрация 2,14 года) размещен на 30%....
10:07

Женский инвестпортфель. Как россиянки зарабатывают на фондовом рынке в 2026 году?
Главное: В 2025 году самыми успешными инвесторами на российском рынке стали женщины По сравнению с мужчинами женщины обычно более...
17:14

Финансовые результаты «Русагро» за 12 месяцев 2025 года
Подводим итоги прошедшего года и делимся наиболее важными событиями. Выручка увеличилась на 17% г/г до 396 млрд руб., обновив рекорд...
14:22

Нефтяной срез: выпуск №8. Перекрытие Ормузского пролива + рост цен на нефть против слабых отчетов за 4-й квартал 2025 и 1-й квартал 2026? Ищем лучших в все еще слабом секторе
Продолжаю выпускать рубрику — Нефтяной срез. Цель: отслеживать важные бенчмарки в нефтяной отрасли, чтобы понимать куда дует ветер. Прошлый пост:...
05 марта 2026, 19:45
теги блога Oleg Mubarakshin ~ Quant-lab
- CBOE
- Derex
- Financial One
- ITinvest
- LSE
- market data
- Microsoft
- option
- option-lab
- options
- quant-lab
- quik
- RTSVX
- RVI
- Si
- SmartX
- SPX
- usd rub
- USDRUB
- volatility
- Ай Ти Инвест
- алготрейдинг
- беня
- брокеры
- вола
- волатильность
- Горчаков
- дельта
- Ильинский
- кванты
- Кирилл Ильинский
- КОНКУРС
- конфа
- конференция
- кукл
- кукловод
- Мартынов
- МОК
- МосБиржа
- Московская биржа
- НОК
- НОК 6
- НОК-7
- обучение
- опцион
- опционы
- отскок
- РЕПО
- роллирование
- спреды
- стаканы
- торговый терминал
- тролинг
- улыбка волатильности
- ФосАгро
- фундаментальный анализ
- хедж
- Чикаго
- экспирация
- юмор



















Историческую волу считаю, чтобы сравнивать ее с имплаид и реалайзд
>> волу посчитанную по 5 (10,15, кому что нравится) -минуткам внутри дня. — это какая?
Нас интересует прогностическая ценность индикатора, а не оценка его дисперсии.
В рамках этих моделей все оценки наверняка являются несмещенными, а несмещенные оценки между собой могут различаться только разбросом оценок вокруг истинного значения. Так что критерий точно не является бессмысленным, но к прогнозированию в реальном мире эти цифры отношения не имеют.
Но в логике создания инструментов прогнозирования ( а любая торговля, кроме гэмблинговой, отражение каких-то способов прогнозирования), под эффективностью хотелось бы понимать меру прогностической ценности оценки.
К сожалению, в математике слова типа «оптимальный» и «эффективный» временами очень далеки от того смысла, который мы в них вкладываем интуитивно.
Использование слов «оптимальный», «эффективный» и так далее без описания критерия и цели его применения я считаю разновидностью манипулирования, если, конечно, тот, кто использует такие слова, реально понимает, что пишет.
Во-первых, ты сравниваешь волатильность, оцененную по дневной OHLC-статистике, с волатильностью, посчитанной внутри дня по 5-10-15 минуткам. Первое, что бы я сделал, это сравнил на истории посчитанную по дневкам (хоть по C_i/C_{i-1}) волу и использованную тобой посчитанную по 5-10-15 минуткам.
Скорее всего, ты выяснишь, что вола, посчитанная по малым таймфреймам в среднем больше, чем посчитанная по дневкам. Это связано с сильной негауссовостью на малых таймфреймах, приводящей к тому, что правило «корень из T» там не работает. Поэтому у тебя образуется множитель для приведения «дневочной» волы к «по-10-минутной», «по-5-минутной» и т.п. (причем, подозреваю, что для каждого малого таймфрейма свой) — больший единицы и позволяющий приводить твои оценки к тому, что ты в измеряешь. После этого выводы о «заниженности» оценок могут измениться.
Ну и во-вторых, в реальном финансовом мире, по моему представлению, мерить второй момент в принципе неправильно. Поскольку реально тебя интересует амплитуда колебаний, а не стандартное отклонение. Вспомни мои любимые устойчивые процессы Леви — дисперсия бесконечна, но опционы под ними отлично прайсятся, если конечно матоожидание. Реальный мир — это все же мир степенных хвостов и второй момент в таком мире — нечто, чего при разумном моделировании может и не быть. Так что лучше везде строить оценки первого абсолютного момента — таково мое убеждение.
1) почему вообще речь про какие то таймфреймы идет, если понятие «вола» мы применяем к опционам? Я не очень уверен, что кто то хеджит «1 раз в t минут», скорее через определенное количество пунктов БА. Если считать «волу» сообразуясь с таким подходом к хеджу, то выбор шага хеджа сильно не влияет на «волу» (в разумных пределах). Правда, есть качественные переходы между «очень маленьким шагом», «разумным шагом», «большим шагом», но это тема отдельная.
2) при чем тут амплитуда? По моему амплитуда и «вола» (как последнюю ни считай) живут почти в разных мирах
Цена опциона по сути своей отражает вероятность того, что цена окажется по некоторую сторону от страйка и величину (амплитуду) отклонения цены от страйка.
А вола есть монотонная функция цены опциона.
А поскольку речь в заметке шла о недооценке/переоценке, то этот фактор может оказаться существенным с точки зрения выводов статьи.
Суть второй части моей ремарки — в том, что с точки зрения нашей опционной жизнедеятельности мне представляется правильнее мерить линейные характеристики силы колебаний, а не квадратичные. То есть E|X|, а не Sqrt(E(X^2)). Напомню, что в случае гауссовского распределения эти 2 величины «идентичны» с точностью до постоянного множителя Sqrt(2/Pi).
Я пояснил в первом сообщении, почему я считаю, что в реальном мире первое измерять правильнее, чем второе. Но это в любом случае вопрос больше веры и философии. Эту точку зрения никому не навязываю, но рекомендую по крайней мере задуматься по этому поводу.
Зато есть общественно-полезное замечание — добавлять в список тэгов слово «опционы», чтобы материал находился по соответствующей ссылке в правой части смарт-лаба :)
«опционы. historical volatility»
А смарт-лаб добавляет в раздел «Опционы» только то, что имеет точный тэг «опционы» — без дополнительных слов