SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. jk555
Цена опциона и Как правильно посчитать дельту?
- 05 ноября 2013, 23:16
- |
Меня всегда не вполне устраивала та дельта опциона, которую можно получить из стандартных формул по всем известным моделям. А нужна она мне для целей хеджирования опционов фьючерсом. Ну не страхует стандартная дельта опционный портфель при движении цены фьючерса так как хотелось, даже если волатильность не меняется.
Попытки строить свои (понятно, что не сам строил – подсматривал у западных коллег. Спасибо французам и американцам) модели так называемой улыбки результат не улучшали. Попытки считать эффективную дельту разными способами тоже не дали желаемый эффект.
Решил забыть все, что знал и начать с начала.
Через некоторое время пришел к своему (подсмотренному у западных коллег и модифицированному) методу расчета стоимости опциона без всяких моделей улыбки волатильности. (Точнее улыбка есть и у меня, ведь можно перевести цены в волатильности.)
Далее было необходимо считать свою дельту. А как?
Я могу посчитать цену опциона при любом фьючерсе. А дельта показывает – на сколько изменится цена опциона при изменении фьючерса на 1 пункт. Т.е. если фьючерс изменится на 1000 пунктов, то опцион подорожавший на 500 пунктов имел дульту 0,5.
И вот, когда я начал считать дельту для опционов таким методом у меня получилось, что иногда, а точнее очень часто опцион имеет ДВЕ!!! Дельты. Почему две? Если цена растет на 1000 то дельта 0,25 например, а если фьючерс падает на 1000 пунктов, то дельта 0,27. Какую дельту брать?
(1000 пунктов взял для примера, исходя из того, что хеджирование будет происходить с таким шагом).
Далее если взять дельту не от того, как измениться цена в моей модели, а посчитать ее исходя из цены в моей модели и цены биржевой, исходя из того, что моя цена справедлива, а биржевая к ней рано или поздно, но придет. То разница в этих дельтах будет иногда еще больше, и может выходить за 1!
Для тестирования я взял оба метода расчета дельты. Так как дельты две (в каждом варианте), то для хеджирования взял среднюю (из каждого варианта). (например (0,27+0,25)/2)
Стратегия и правила когда и что купить описаны в предыдущих постах, ссылки ниже.
Итак вот Эквити:
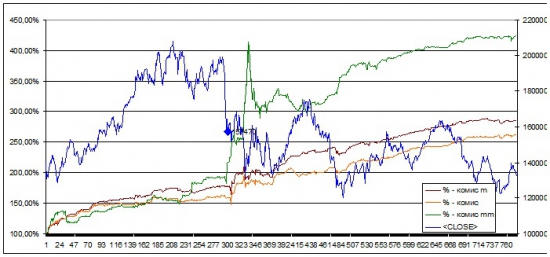
Оранжевая линия – обычная дельта.
Коричневая линия – дельта по моей модели оценки опционов.
Зеленая линия – дельта по моей модели относительно текущих биржевых цен.
Синяя линия – цена фьючерса на индекс РТС.
Сразу примечание/дополнение:
1.Стартовая сумма 1200000 пунктов.
2.Рехеджирование каждый час, как и раньше.
3.Гарантийное обеспечение в учет не принималось (приму чуть ниже не на автомате)
4.Дельта для хеджирования внутри дня считалась по времени до экспирации на следующий час с шагом для фьючерса 1000 пунктов.
5.Дельта для хеджирования через ночь считалась по времени до экспирации на следующий день с шагом для фьючерса 5000 пунктов.
6.Волатильность из архива биржи (A) (что не совсем корректно).
7.Метод «ухода от риска» описан в предыдущих постах (это объясняет почему нет сильной просадки при резком росте волатильности — позиции в этот момент нет. иногда спасает.)
8.Шкала внизу это дни.
Визуально видно, что хеджирование своей дельтой дает положительный эффект.
Теперь по поводу резкого роста, и такого же славного падения зеленой линии на графике..
1.Волатильность была высока.
2.Опционы были сильно переоценены относительно моих цен, что искажает дельту. (шорт по фьючерсу был очень большой, отсюда и рост Эквити при падении)
3.ГО было высоким
Исходя из этого:
Позиция скорее всего в этот момент была реально раза 4 меньше по объему, т.е. ни такого резкого роста Эквити, ни последующего падения на 40% не было бы. Т.е. Эквити с 300 по 350 дни будет другим.
Плюс в такие периоды нужно как-то учитывать, что волатильность будет снижаться, и дельта реально должна быть другой.
График просадки:
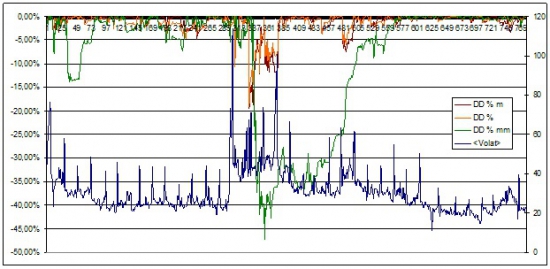
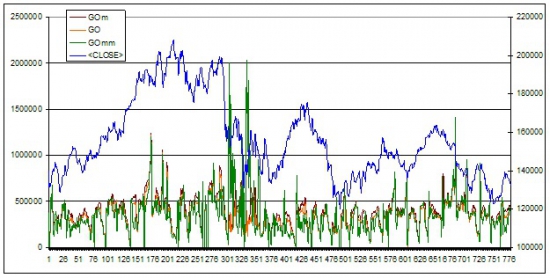
График ГО:
Комментарии приветствуются!
Предыдущие посты на тему опционов:
Продажа опционов. Построение арбитражной стратегии.
http://smart-lab.ru/blog/124999.php
Оптимизация стратегии. Арбитраж волатильности.
http://smart-lab.ru/blog/126805.php
Тестирование опционных стратегий в Excel
http://smart-lab.ru/blog/114286.php
http://smart-lab.ru/blog/114221.php
P.S. Отдельное спасибо за вариант расчета ГО © Simix.
smart-lab.ru/blog/147536.php
Попытки строить свои (понятно, что не сам строил – подсматривал у западных коллег. Спасибо французам и американцам) модели так называемой улыбки результат не улучшали. Попытки считать эффективную дельту разными способами тоже не дали желаемый эффект.
Решил забыть все, что знал и начать с начала.
Через некоторое время пришел к своему (подсмотренному у западных коллег и модифицированному) методу расчета стоимости опциона без всяких моделей улыбки волатильности. (Точнее улыбка есть и у меня, ведь можно перевести цены в волатильности.)
Далее было необходимо считать свою дельту. А как?
Я могу посчитать цену опциона при любом фьючерсе. А дельта показывает – на сколько изменится цена опциона при изменении фьючерса на 1 пункт. Т.е. если фьючерс изменится на 1000 пунктов, то опцион подорожавший на 500 пунктов имел дульту 0,5.
И вот, когда я начал считать дельту для опционов таким методом у меня получилось, что иногда, а точнее очень часто опцион имеет ДВЕ!!! Дельты. Почему две? Если цена растет на 1000 то дельта 0,25 например, а если фьючерс падает на 1000 пунктов, то дельта 0,27. Какую дельту брать?
(1000 пунктов взял для примера, исходя из того, что хеджирование будет происходить с таким шагом).
Далее если взять дельту не от того, как измениться цена в моей модели, а посчитать ее исходя из цены в моей модели и цены биржевой, исходя из того, что моя цена справедлива, а биржевая к ней рано или поздно, но придет. То разница в этих дельтах будет иногда еще больше, и может выходить за 1!
Для тестирования я взял оба метода расчета дельты. Так как дельты две (в каждом варианте), то для хеджирования взял среднюю (из каждого варианта). (например (0,27+0,25)/2)
Стратегия и правила когда и что купить описаны в предыдущих постах, ссылки ниже.
Итак вот Эквити:

Оранжевая линия – обычная дельта.
Коричневая линия – дельта по моей модели оценки опционов.
Зеленая линия – дельта по моей модели относительно текущих биржевых цен.
Синяя линия – цена фьючерса на индекс РТС.
Сразу примечание/дополнение:
1.Стартовая сумма 1200000 пунктов.
2.Рехеджирование каждый час, как и раньше.
3.Гарантийное обеспечение в учет не принималось (приму чуть ниже не на автомате)
4.Дельта для хеджирования внутри дня считалась по времени до экспирации на следующий час с шагом для фьючерса 1000 пунктов.
5.Дельта для хеджирования через ночь считалась по времени до экспирации на следующий день с шагом для фьючерса 5000 пунктов.
6.Волатильность из архива биржи (A) (что не совсем корректно).
7.Метод «ухода от риска» описан в предыдущих постах (это объясняет почему нет сильной просадки при резком росте волатильности — позиции в этот момент нет. иногда спасает.)
8.Шкала внизу это дни.
Визуально видно, что хеджирование своей дельтой дает положительный эффект.
Теперь по поводу резкого роста, и такого же славного падения зеленой линии на графике..
1.Волатильность была высока.
2.Опционы были сильно переоценены относительно моих цен, что искажает дельту. (шорт по фьючерсу был очень большой, отсюда и рост Эквити при падении)
3.ГО было высоким
Исходя из этого:
Позиция скорее всего в этот момент была реально раза 4 меньше по объему, т.е. ни такого резкого роста Эквити, ни последующего падения на 40% не было бы. Т.е. Эквити с 300 по 350 дни будет другим.
Плюс в такие периоды нужно как-то учитывать, что волатильность будет снижаться, и дельта реально должна быть другой.
График просадки:

График ГО:

Комментарии приветствуются!
Предыдущие посты на тему опционов:
Продажа опционов. Построение арбитражной стратегии.
http://smart-lab.ru/blog/124999.php
Оптимизация стратегии. Арбитраж волатильности.
http://smart-lab.ru/blog/126805.php
Тестирование опционных стратегий в Excel
http://smart-lab.ru/blog/114286.php
http://smart-lab.ru/blog/114221.php
P.S. Отдельное спасибо за вариант расчета ГО © Simix.
smart-lab.ru/blog/147536.php
2.5К |
Читайте на SMART-LAB:

Обзор рынка облигаций
Если не считать бури вокруг Евротранса, то неделя прошла спокойно. Рынок продолжает взвешивать ситуацию с дефицитом бюджета и способами...
14:55
Как устроен бизнес ДОМ.PФ? Рассказываем в интервью
☝️ Говорим на сложные темы простым языком 🔵Как устроен бизнес ДОМ.PФ? 🔵Кто сегодня инвестирует в компанию? 🔵Что в планах на ближайшее...
14:19
теги блога jk555
- DAX
- ipad
- Market Sentiment
- Sentiment
- Si
- xCFD
- акции
- Александр Михайлович
- анализ торговой системы
- аналитик
- аналитики
- Андрей Верников
- арбитраж
- банки
- биржа
- будущее
- Василий Олейник
- волатильность
- время - деньги
- газ
- Гном
- дельтахеджирование
- дисциплинированный трейдер
- доверительное управление
- доллар
- закон
- инвестирование
- инвестиции
- индекс ММВБ
- индикатор
- интрадей
- исследование
- история жизни
- итоги 2013
- итоги месяца
- клуб
- КОНКУРС
- кризис
- ликвидность
- лчи
- ЛЧИ 2013
- лчи 2014
- ММ
- Московская биржа
- настроение рынка
- нефть
- обвал
- обучение
- опрос
- оптимизация
- опционы
- опыт
- параметры
- паттерны
- Пенза
- перспективы
- планка
- поводырь
- портфель
- прогноз
- прогноз по рынку
- прогнозы
- продажа волатильности
- революция
- рейтинг
- робот
- роботы
- РТС
- рубль
- рыночный сентимент
- сентимент
- сентимент рынка
- спекулянты
- спрэды
- стратегии
- стратегия
- стратегия спекуляции
- тестинг стратегии
- Тестирование стратегий
- толпа
- Торговля без стопов
- трейдер
- трейдеры
- трейдинг
- Украина
- улыбка
- улыбка волатильности
- Управление капиталом
- фундаментальная оценка
- фьюерс ртс
- фьючерсы
- хеджирование рисков
- цитаты
- шорт
- шорт RI
- эмоции





















ибо это случайно блуждающая в неком диапазоне величина на некоем конечном промежутке времени )
сугубо ИМХО!
но за саму попытку исследования +
Очень тяжело было переводить труды на французском… Зато в РФ почти все диссертации на тему опционов переписаны с одной работы.
Вот пример реализации на RI, где каждая точка улыбки учитывает определенное движение цены за срок.
optionanalyser.livejournal.com/10511.html
Выше там же еще несколько ссылок на др. методы.
да прям так и написано в точности как у вас.
and so on…
да
это что у него названо «modified delta»
Dynamic Hedging, page 118.
its obvious — just hedge options with options :)
ну а иначе (в смысле если линейным БА хеджировать) то да — «вертолёт», зависимость от шага и всё такое прочее) от этого никак не уйти
БА в силу на порядок большей ликвидности можно считать линейным, т.е. аналоговым…
все опции как вторые производные и менее ликвидные получаются в итоге как бы дискрентно/цифровыми, т.е. по сути бинарными с той или иной степенью дискретизации…
в физике полно таких процессов и они в основном описываются преобразованием Фурье и всем таким…
и в рынке можно описать всё что угодно, особенно задним числом )
но вся проблема в том что в рынке никогда НЕТ чётких границ диапазона, а в физике они ЕСТЬ!
ибо ограничены всякими константами по гравитации и всем таким…
вот это основное различие, поэтому рынок может описываться тока вероятностно…
ну в общем кому надо поймёт и как обычно всё ИМХО )
если умеем моделировать динамику улыбки, то производные с этого дела всегда возьмём. вопрос в моделировании… большая и творческая тема)
Евгений (jk555), а акция это опцион на активы всего лишь… )
Тут искренне браво
Дай Бог век прожииву и учиться буду
Само бы в голову не пришло)
Если не секрет то о каких трудах западных колег идет речь?
Я искал форумы и сайты квантов и все о квантах в различных поисковиках, гугл в первую очередь, на разных языках. Первые несколько недель поисков давали ссылки на сплошной мусор, потом нахватавшись нужных отрывков начал писать правильные запросы. :) Читал книги, статьи в журналах, смотрел выступления… в общем инфы было много, большую часть просто забыл сразу, т.к. для меня пользы от нее не было.
Да и фамилии я никогда не запоминаю.
По логике, НИЧЕГО, кроме цены опциона оценивать и не нужно. Все остальное — оценки параметрических моделей, так или иначе основанных на локальной полиномиальной аппроксимации цены опциона.
А Вы что, собственно оцениваете?
Я понимаю, что в том, как Вы это делаете, есть ноу-хау, поэтому и не спрашиваю.
По идее твои исследования показывают что надо брать не просто улыбку для расчёта дельты, а её производную по БА. В старом журнале F&O про это была целая статья. Логически понятно что если БА пойдёт вниз, то вола более вероятно подымется, а если вверх, то упадёт. Функцию расчета улыбки ртс мы знаем, по идее надо брать её аналитическую производную ну или просто ограничиться наклоном касательной в точке БА.
Вот полюбуйтесь
forum.option.ru/index.php?showtopic=909&st=0&p=5262&#entry5262
В моей модели есть только одна волатильность на все опционы и она одинакова для всех страйков. Т.е. в расчете дельты никакая улыбка участие не принимала, и тем более не учитывалось изменение волатильности. Я пока не стал брать и добавлять сюда функцию волатильности, которая тоже у меня есть. Очевидно, если учитывать возможное изменение волатильности, то делать это нужно независимо от улыбки. Я собираюсь пересчитывать биржевые цены в свою волатильность и сравнивать со своей моделью. Наверно так будет правильней. Иначе функция волатильности будет искажаться излишним спросом или предложением, т.е. IV, которая по факту не влияет на HV в моменте.
А вообще, с волатильностью все не просто. Она как бы интегрирует амплитуду краткосрочных колебаний и их интегральную направленность тоже.
Можно, используя стандартную трехточечную симметричную схему получить оценку первой и второй производной и все станет на свои места.
Правда, если исходная функция оценена не слишком точно, возникают хитрые нюансы, к которым уже нет общего подхода.
Мое представление по сути дельтахеджированию:
1. положительный результат от продажи опционов заложен в их «завышенной» цене по причине большего риска.
2 как дельту не считай результат в конкретном месяце будет зависеть от того, как структура движения БА ляжет на вашу систему хеджирования.
3. Хочу поделиться своим «велосипедом» :)))
Хеджирование делать " с плечом" меньше 1 (например 0,8)
при сильном движении БА догонять до 1
Это дает возможность в небольшом временном промежутке собирать тету (т.е вовремя нужно будет закрыть позицию).
При долгом удержании позиции никаких положительных моментов не дает.
Еще одна наработка по продаже опционов:
Когда вы залезли в такую позицию и вдруг (как всегда неожиданно) выросла волатильность.То вы попадаете в ситуацию — либо откупаться по высоким ценам, либо пилиться своим хеждированием до больших минусов, или если позволяют средства добавить позицию по более высоким ценам.
Я изначально предлагаю хеджировать волатильность более дальними по времени опционами. Объемы покупки/продажи и комиссии больше для создания такой позиции, но в случае чего можно выскочить из нежелательно возросшей волатильности.
quant-lab.com/research/poc-6-summary-of-my-presentation.html
У нас хеджеров то нет…
С другой, восхищаюсь темпами прогресса)) На самом деле, еще чуть-чуть и останутся лишь барьерные и прочая экзотика.
Что касается темы, то в качестве решения проблемы можно предполагать, что есть два распределения — вверх и вниз, которые связаны с различным набором параметров для различных типов движения и режимов рынка. Посколько невозможно предположить направление, невозможно добиться и эффективного хеджа.
Но тут есть другой аспект, который заключается в том, что рынок обычно содержит премию не только в первом моменте, но и 2, 3 и 4м тоже. Более того, персистентность премии на разных активах разная. Если вкратце)
-эффективного невозможно, но к более эффективному нужно стремиться :) к тому-же в разные моменты при различных перекосах, наверно, стоит их учитывать.