Andrey Morozov
GBPUSD лонг
- 11 июля 2016, 18:16
- |
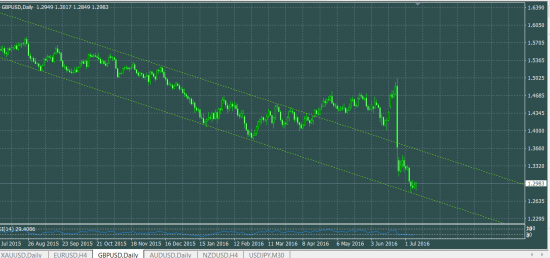
На H4 вроде как наклевывается прорыв трендовой
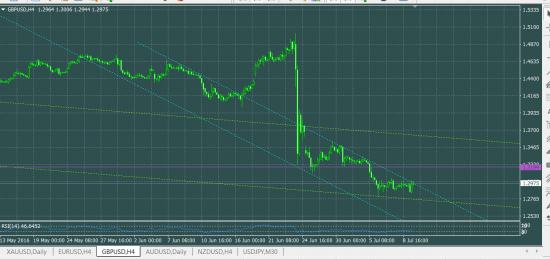
( Читать дальше )
- комментировать
- ★2
- Комментарии ( 36 )
Закон малых чисел (интересный копипаст)
- 11 июля 2016, 15:22
- |
neveev.ru/Mind%20traps/cognitive%20biases/law%20of%20small%20numbers/
Александр Невеев кандидат психологических наук
Термин «закон малых чисел» (law of small numbers), введенный в научный обиход нобелевским лауреатом и психологом Даниэлем Канеманом, как и исходный термин «закон больших чисел» (law of large numbers), условны, и их не стоит трактовать буквально.
Что же это за закон такой — закон малых чисел?
Чтобы ответить на этот вопрос, нам нужно ненадолго сосредоточиться на законе чисел больших.
А закон больших чисел, говоря предельно упрощенно, касается вот чего.
Допустим у нас есть огромный мешок с российскими монетами достоинством 1 рубль, 2 рубля, 5 рублей и 10 рублей. В мешке этих монет бесконечно много, причем монет каждого достоинства поровну. Предположим, что эти монеты не отличаются по размеру и весу. К мешку по очереди подходят люди и вынимают каждый по одной монете. Это происходит снова и снова: огромное количество людей получают свои монеты.
Наша задача — угадать, сколько денег получит каждый подошедший в среднем.
( Читать дальше )
USDJPY
- 10 июля 2016, 20:56
- |
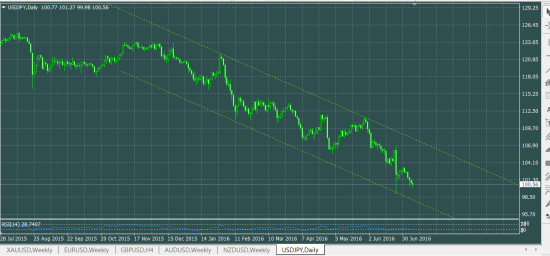
На H4 варианты
флет с узким диапазоном
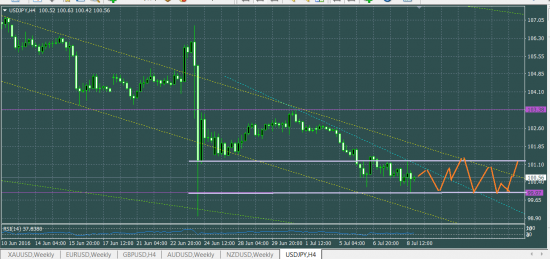
( Читать дальше )
XAUUSD
- 09 июля 2016, 14:37
- |
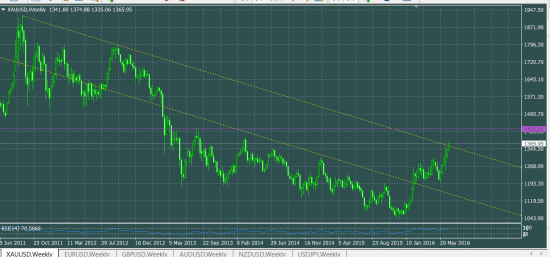
На днях нонфармы откорректировали цену до 23 фибо.
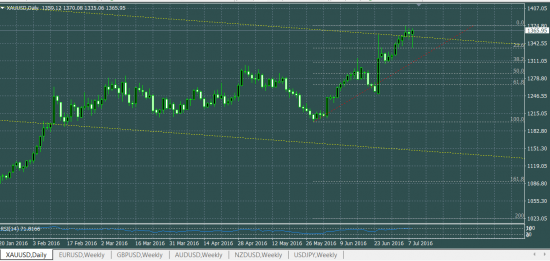
( Читать дальше )
USDCAD
- 06 июля 2016, 08:24
- |

На дневном графике ничего особенного я не увидел.
.
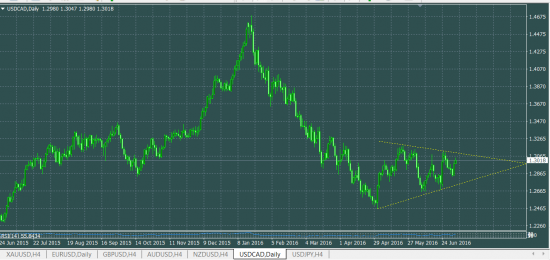
( Читать дальше )
EURUSD
- 02 июля 2016, 19:32
- |

На H4 можно поискать продажи вот по такому сценарию.

( Читать дальше )
XAUUSD
- 02 июля 2016, 15:23
- |

теги блога Andrey Morozov
- bitcoin
- EUR USD
- eurrub
- eurusd
- eurusd forex
- eurusd евра
- forex
- fRTS
- fRTS Short
- Gbp Usd
- GBPUSD
- InstaForex
- nzdusd
- RTS
- S&P500
- SI
- USDCAD
- USDX
- австралиец
- биткоин
- Веселье
- ВТБ
- Доллар Рубль
- евро
- Евро доллар
- евродолар
- евродоллар
- евродоллар eurusd
- евродоллар eurusd торговый сигнал
- золото
- Золото Gold
- индек доллара
- индекс доллара
- инстафорекс
- как стать богатым
- Крах
- криптавалюта
- криптовалюта
- мобильный пост
- нефть
- общее
- околорынок
- оффтоп
- политика
- психология
- психология трейдинга
- психология в трейдинге
- психология трейдинга
- Ри
- РТС
- теханализ
- технический анализ
- торговые платформы
- торговые сигналы
- третья мировая война
- Украина
- фо
- Форек
- форекc
- форекс
- форекс forex
- ФРС
- фРТС
- Фунт
- фунт доллар
- фьчерс РТС
- фьюерс ртс
- фьючер на индекс РТС
- Фьючерс на индекс РТС
- фьючерс РТС индекс РТС
- хомяк
- экономика
- юмор
- юмор веселье


























