Блог им. EkaterinaKutnyak
Как рассчитать дюрацию «на коленке». Часть 4
- 19 декабря 2023, 00:06
- |
Это уже четвертый пост о расчетах в EXCEL, связанных с облигациями. На этот раз о том, как рассчитать НКД и дюрацию, не используя встроенных формул.
Напомню, что все встроенные «облигационные» формулы рассчитывают все показатели, когда купоны выплачиваются 1, 2 или 4 раза в год. А что желать с теми 250+ выпусками, где купоны платят каждый месяц?
Для этого придется вспомнить формулы, как это не грустно.
Ну, с НКД все достаточно просто. Возьмем для примера выпуск с выплатой купона 12 раз в год и амортизацией. Бумаги с амортизацией тоже приходится считать руками. Встроенные функции ее просто не видят.
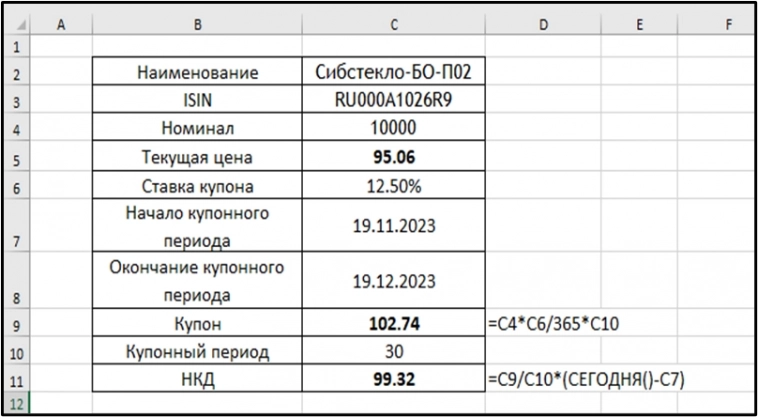
Рассмотрим выпуск Сибстекло-БО-П02. Здесь есть все, что нам нужно.
Цена текущая подтягивается с биржи (смотри предыдущие посты). Значение купона в рублях рассчитываем по формуле ниже (Ячейка С9).
Где
Coupon — размер купона
N – номинал облигации
rc – купонная доходность в % годовых
tc – длина купонного периода
Зная значение купона и длину купонного периода, легко рассчитать НКД, используя функцию СЕГОДНЯ (Ячейка С11).
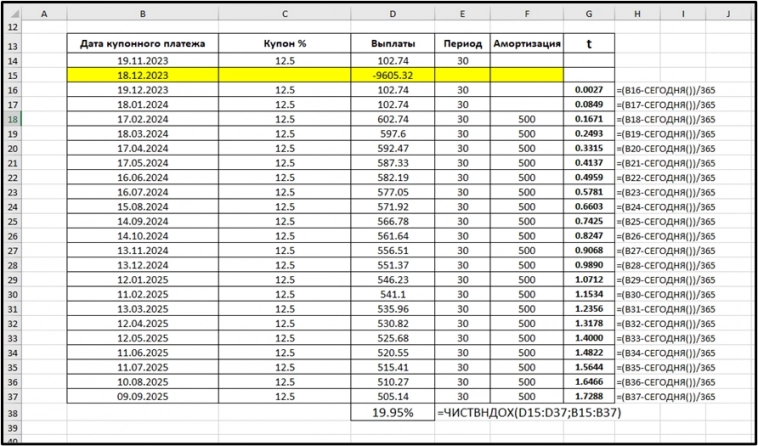
Для того, чтобы рассчитать дюрацию, нам нужна доходность к погашению В ее расчете ничего не меняется. Функции ЧИСТВНДОХ все равно, что считать. Главное правильно записать поток платежей.
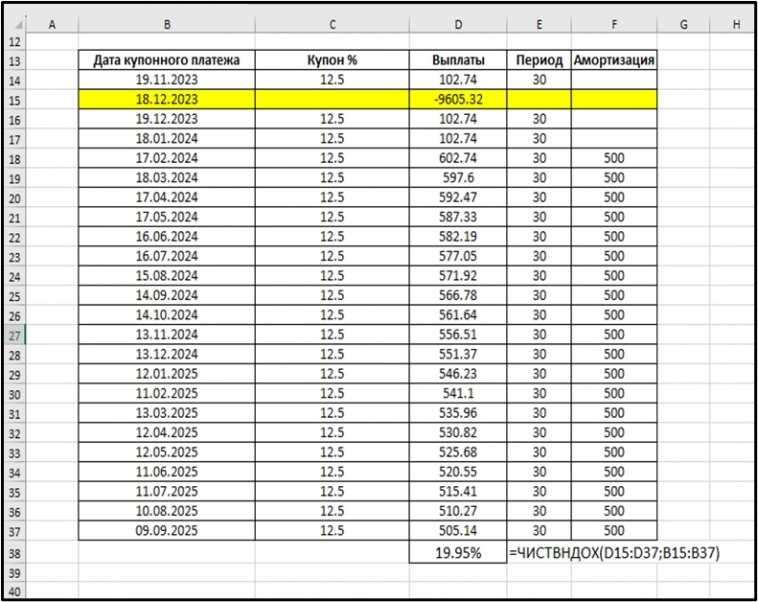
С учетом амортизационных выплат поток платежей выглядит следующим образом. Здесь я не считаю новый размер купона после каждой выплаты. Я использую то, что есть в свободном доступе. Просто каждый раз к купону прибавляется еще и амортизационный платеж.
Доходность к погашению эффективную мы уже считали. Если есть поток платежей и даты, то лучшее решение это функция ЧИСТВНДОХ.
Дюрация Маколея считается по формуле:
Где
PV х t – приведенная стоимость всех потоков платежей, взвешенных по времени
P – текущая цена облигации
Выглядит жутко, но по сути ничего ужасного.
Для начала нужно вычислить все t. Это периоды в годах от текущей даты до очередной выплаты.
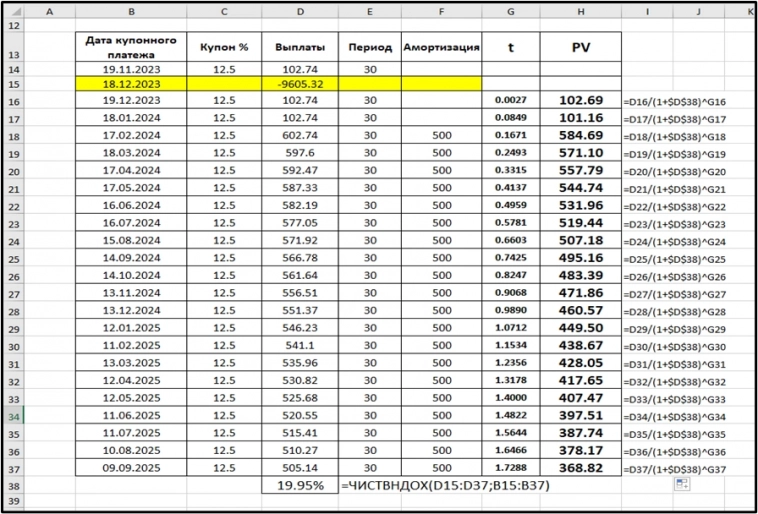
Теперь нам нужно найти значение PV. Это дисконтированные, приведенные к текущей дате, потоки платежей по облигации. В качестве ставки дисконтирования используем доходность к погашению.
То есть каждый платеж мы дисконтируем на ставку доходности к погашению в степени t.
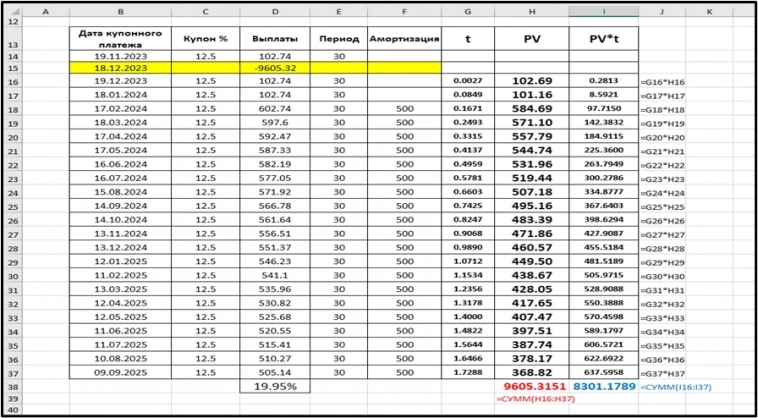
Теперь перемножаем tиPVи находим сумму перемноженного.
А цена облигации Р, есть не что иное, как сумма всех дисконтированных платежей.
Теперь «синенькое» PV*t делим на «красненькое» P, и получаем дюрацию Маколея. Дюрация = 0.86.
Модифицированную дюрацию найти несравнимо проще. Формула модифицированной дюрации:
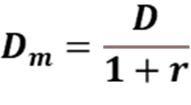
Где
D – дюрация Маколея
r – доходность к погашению облигации.
То есть в этом примере, Dm= 0.86/ (1+19.95%) = 0.72
t.me/kutnyak_invest


теги блога Ekaterina Kutnyak
- Excel
- p/e
- акции
- Альфа-Банк
- валюта
- вероятности
- дивиденды
- доходности облигаций
- дюрация
- замещающие облигации
- Итоги недели
- Книги
- мнения
- мультипликаторы
- НКД - накопленный купонный доход
- обзор рынка
- облигации
- оферта
- оферта миноритариям
- оферта по облигациям
- Портфель инвестора
- психилогия
- психологические ошибки
- расчет
- расчёт риска
- рецензия на книгу
- риск
- рынок
- ставка рефинансирования
- трейдинг
- учет портфеля
- флоатеры



















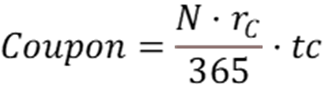
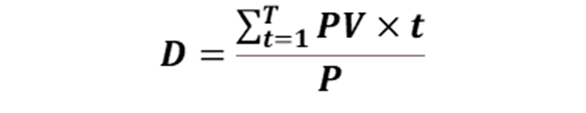


Если в предложенном подходе заложена более глубокая идея, которую не увидел, прошу возразить.