Остаться в живых (или когда последние становятся первыми)

Какой шаг самый трудный на шатком мосту? Первый или последний? Тот, что я сделаю прямо сейчас,  ведь только его я могу выбрать. А первый шаг может стать для меня и последним (неизвестный даос)

«Твой номер шестнадцатый, помалкивай в трубочку! Ясно?!» из к/ф «Место встречи изменить нельзя»

В седьмой серии культового сериала “Игра в Кальмара” герои приняли участие в испытании “Хрустальный мост через реку” Каждая из ступеней (панелей) этого моста представляла собой две стеклянных пластины, одна из закалённого стекла, а другая  — из обычного. Всего таких ступеней было 18, а участников игры, оставшихся в живых к этому моменту  — 16.

Перед началом игроки выбрали свои порядковые номера, еще не догадываясь о том, что их ждёт впереди. Ужас и растерянность, охватившие мужчину, которому выпало стать первопроходцем, совершенно понятны — число возможных траекторий составляет для него 2 в 18-ой степени, и только в одном случае ему удастся пройти весь путь невредимым. Это один шанс из 262144.

Сделаем несколько общих замечаний. Игра устроена таким образом, что каждый участник торит дорожку для того, кто идет за ним, и даже если он в какой-то момент наступит на хрупкую пластинку, то «разблокирует» эту панель для следующего в очереди. Мы считаем, что все игроки запоминают «ходы», сделанные их предшественниками. Следовательно, игрок с номером n может быть уверен, что как минимум первые n-1 ступеней станут для него открытой книгой, т.е. он пройдет их со стопроцентной вероятностью. А если этому игроку удастся дойти до последней панели, мост автоматически пройдут и все последующие N-n участников. Самые высокие шансы выжить у последнего игрока (и об этом догадывается любой партизан, прогоняющий стадо коров через минное поле, прежде чем его перейти) Но насколько они велики? И каково ожидаемое число уцелевших игроков?

Легко заметить, что вероятность пройти мост для самого последнего игрока совпадает с вероятностью выживания хотя бы одного участника. А значит она равна 1 — P(0), где P(0) — вероятность того, что погибнут все. Легче всего рассчитать вероятности, если число панелей M равняется общему количеству игроков N (мы не рассматриваем случай, когда  N > M, так как в этом случае очевидно, что вероятность выжить для последних N — M     игроков равна единице). Несмотря на то, что наши «испытания» существенно зависимы, т.е. вероятность пройти мост для каждого из героев зависит от результата предшественников, можно показать, что в случае M=Nчисло выживших участников подчиняется биномиальному распределению  B(N,p)с вероятностью успеха  p=1/2.

Для этого удобно предварительно рассмотреть события того, что ровно k игроков будут устранены из игры к моменту ее завершения. При условии, что провалились k ≤ M игроков, существует C(M, k) способов распределить k разбитых стеклянных пластин среди M панелей, а вероятность любой отдельной комбинации равна (1/2)ᴹ (здесь мы применяем теорему умножения вероятностей зависимых событий) Затем мы воспользуемся симметрией биномиального распределения при p = 1/2.

Оказывается, что шансы для последнего номера невероятно растут с увеличением общего количества игроков (и числа панелей, соответственно) Для 16-ти игроков и 16-ти ступеней эта вероятность очень близка к 1, она равна 0.9999847. Среднее число выживших в этом случае равно N/2, т.е. 16/2=8. Это немало.

Если панелей больше, чем игроков (M>N), распределение вероятностей числа «победителей» можно рассчитать, используя рассуждения, аналогичные тем, что мы проводили с игроками-неудачниками.

В этом случае вероятность того, что выживут ровно n участников равна

                      P(n) = C(M, N — n)(1/2)ᴹ   если   0<n≤N;

          P(n) = sum{j=N to j=M} [C(j-1,N-1)(1/2)ʲ]   если   n =0.

Мы видим, что с увеличением количества панелей картина становится чуть менее радужной, но для 18 (и даже 24) ступеней шансы последнего участника победить всё равно остаются очень высокими, и он выживет с вероятностью свыше 90%.

На рис. 1 показаны примеры распределения числа выживших игроков для 16-32 панелей, где точками обозначены вероятности, что мост пересекут ровно n игроков. Видно, что с ростом числа панелей центр распределения едет влево, и его левый хвост наливается кровью разбившихся жертв.

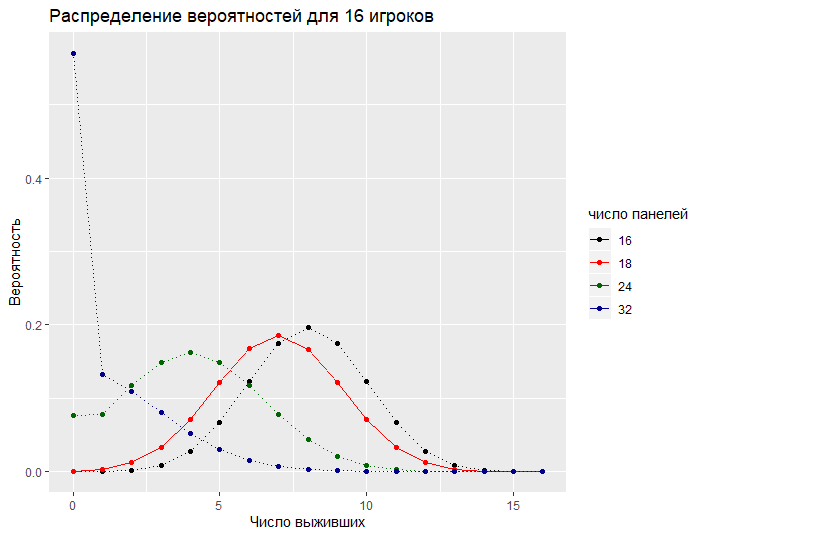
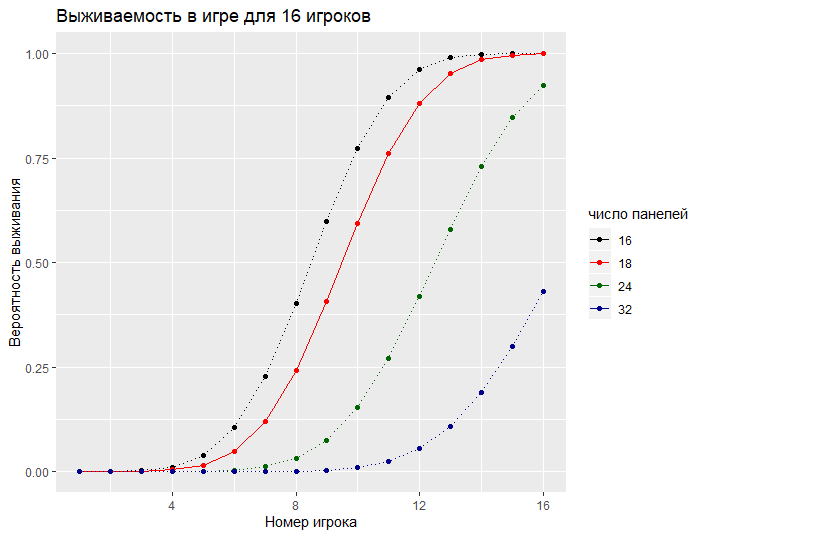
Вероятность выживания для участника с номером n это кумулятивная вероятность того, что   n — 1 остальных будут устранены из игры, т.е. это сумма Q(0) +...Q(n-1), где Q(i) — вероятность того, что погибших окажется ровно i. Из рис. 2 видно, что даже если число панелей вдвое превышает общее количество игроков, вероятность выживания для последнего номера составляет немногим менее 50%

На последнем рисунке представлена зависимость среднего числа E(n) выживших от количества стеклянных панелей:

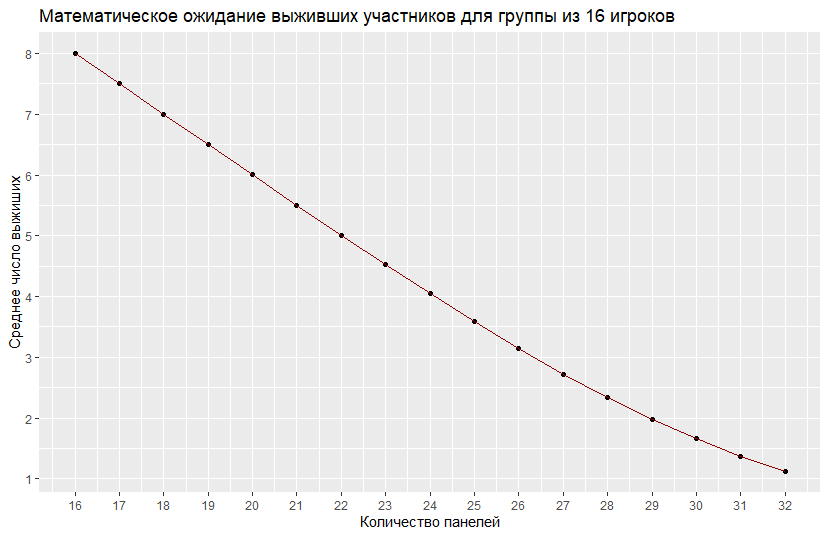
Например, для 18 панелей (как это устроено в сериале) матожидание практически равно 7. Это почти в два раза больше числа спасшихся в 7-й серии (их оказалось 3 человека) Такая разница легко объясняется несовершенным поведением людей в сериале: часть забывала путь, по которому уже прошли другие, а кто-то решил покончить с собой и прихватить на тот свет своего врага.

 
Игра «Хрустальный мост через реку» крайне несправедлива — участник с большим номером имеет лучшие шансы на выживание. Но можно провозгласить социализм и ввести уравниловку. Дело в том, что одна закалённая пластина может выдержать вес двух игроков. Поэтому игроки могут пропускать очередь вперёд: например, если 1-й номер прыгнул и не разбился, он приглашает на свою пластину номер 2 и уже тот прыгает на следующую панель. Если не разбился и он, приглашается 3-й, который перепрыгивает 1-ю и 2-ю закаленную пластины, чтобы «проверить» 3-ю. Таким образом, первые в очереди игроки получают равные шансы на выбывание. Понятно, что в реальной игре на такое никто не согласится. Или же свое место в очереди можно продать? Какова стоимость места для игрока с номером n, если он нейтрален к риску? Предлагаю читателю самостоятельно поразмыслить над этой несложной проблемой.