SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Теория и Практика Дельта-Хеджа
- 26 января 2020, 12:41
- |
Для того, чтобы продать волатильность, нам необходимо продать стрэддл — этим, мы полностью избавляемся от чувствительности к направлению движения цены, оставляя при этом чувствительность к «волатильности»… Чтобы не запутаться, обозначим первую волатильность за IV (Implied Volatility) и будем считать её заранее известной и эффективной.
Если бы рынок был монеткой и выходил бы на экспирацию двумя возможными вариантами {+IV, -IV }, то результатом продажи нашей опционной конструкции был бы ровно 0, в силу равенства IV=RV. Но рынок выходит на экспирацию через «тренды» и «пилы», которые выводят Базовый Актив в том числе далеко за ± IV, и в том числе и в ноль. В результате, конечное отклонение от ± IV и, соответственно, риски, которые мы принимаем при продаже стрэддла, составляют приблизительно :
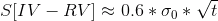
где S — СКО, RV ( «реализованная волатильность») - отклонение цены на экспирацию, t — время до экспирации, а сигма0 — величина шага движения цены. Это уравнение можно получить численно, а можно, взяв интеграл по соответствующему распределению Гаусса (аналитический вариант).
Теперь рассмотрим наш стрэддл несколько повнимательней:
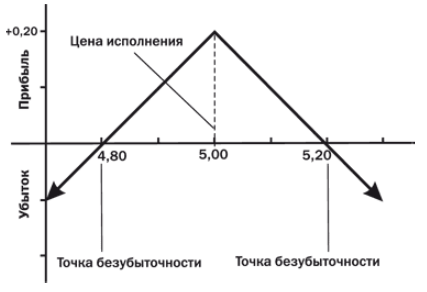
Наш стрэддл имеет две длинные ноги, имеющих дельту ± 1 (для простоты считаем тетта=0), и легко хеджирующихся такими же фьючерсами, и одну особую точку — центральный страйк, для которого дельта (первая производная по цене) = 0, но гамма (вторая производная по цене) = -20, и она уже фьючерсами никак не хеджируется. Для простоты, конечно, мы полагаем, что цена изменяется как-то дискретно с некоторым шагом H (10 центов на рисунке).
И как бы мы не хотели захеджировать эту особую точку — мы этого сделать не можем, так как контр-инструмент, то есть фьючерс, не обладает никакой гаммой и не в состоянии её захеджировать (хеджирование опционами мы не рассматриваем). При этом, сколько бы наша дельта не стремилась здесь к нулю, из-за существования гаммы наша конструкция все равно остаётся чувствительной к изменению цен БА*.
* В этом смысле, стоимость опциона это отнюдь не стоимость его дельта-хеджа.
Теперь, чтобы рассчитать предельную (конечную) эффективность идеального дельта-хеджирования, нам нужно всего лишь рассчитать неопределённость или риски, связанные с гаммой. Для чего, сначала рассчитаем среднее время пребывания нашего стрэддла на ЦС:
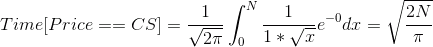
где N — время до экспирации в единицах интервала рехеджа, равное числу изменений цены или числу рехеджей.
Полученное время есть, в свою очередь, случайная величина, для которой, можно записать:
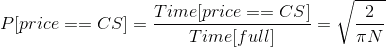
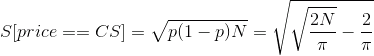
(вышеприведенные результаты подтверждены моделированием)
Теперь, поскольку мы полностью захеджировали риски в иных ситуациях, то оставшиеся после дельта-хеджа риски составят:
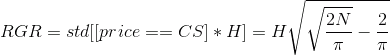
где RGR — остаточный гамма-риск (Residual Gamma Risk), H — шаг дельта-хеджирования, N — количество шагов до экспирации.
Переходя к непрерывному случаю и, учитывая вид 2-ого члена в разложении Тейлора, получим выражение для непрерывного остаточного гамма-риска :
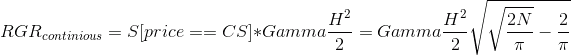
Таким образом, мы получили теоретический предел сжатия рисков при помощи дельта-хеджирования. Изобразим полученную зависимость графически:
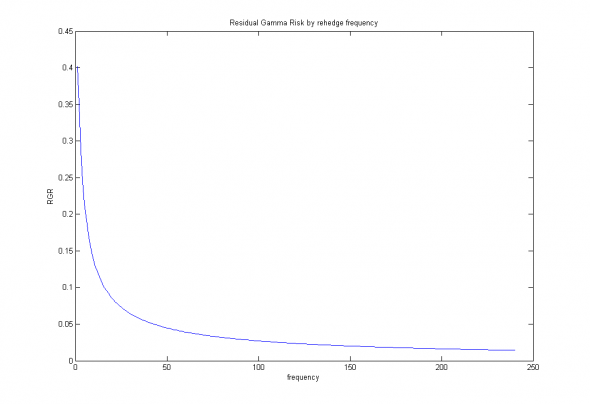
Иллюстрация. Зависимость остаточных рисков от частоты дельта-хеджирования.
Теперь сравним полученное теоретическое значение с экспериментальным, захеджировав по 10 000 стрэддлов, длительностью 15, 60 и 240 шагов (дней) при помощи одного из моих алгоритмов хеджирования, при априорно заданных IV=H=1.
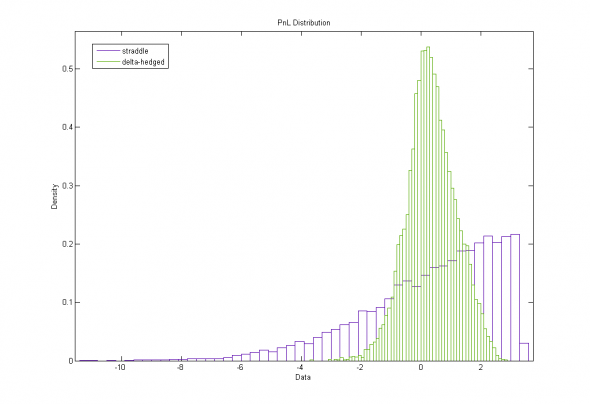
Рис. 1. Стрэддл на 15 дней, 10 000 симуляций :
Теоретический Риск стреддла = 2.32 , Эмпирический результат = 2.24
Остаточный Гамма-Риск (теория) = 0.78, Эмпирический результат = 0.81
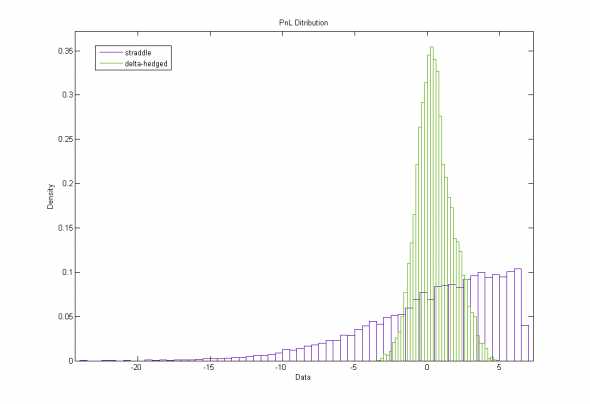
Рис. 2. Стрэддл на 60 дней, 10 000 симуляций :
Теоретический Риск стреддла = 4.64, Эмпирический результат = 4.63
Остаточный Гамма-Риск (теория) = 1.18, Эмпирический результат = 1.26
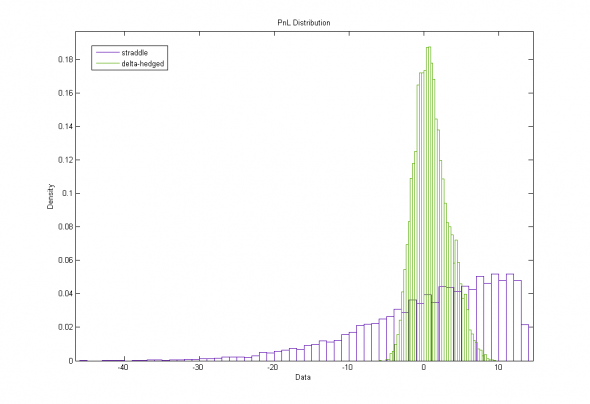
Рис. 3. Стрэддл на 240 дней, 10 000 симуляций :
Теоретический Риск стреддла = 9.29, Эмпирический результат = 9.22
Остаточный Гамма-Риск (теория) = 1.71, Эмпирический результат = 2.29
4.4К |
Читайте на SMART-LAB:
Российский рынок уходит на праздники в зеленом
Торги 20 февраля на российских фондовых площадках проходили в умеренном плюсе на небольших объемах. Номинированный в рублях индекс Мосбиржи к...
17:53
Обновление кредитных рейтингов в ВДО и розничных облигациях (ООО "Урожай" и ООО "ЦЕНТР-РЕЗЕРВ" присвоен статус "Под наблюдением", ООО «ХРОМОС Инжиниринг» подтвердил ruBB)
🔴ООО «УРОЖАЙ»
АКРА присвоило статус «Под наблюдением» кредитному рейтингу BB-(RU) «Урожай» — небольшой региональный производитель зерновых и...
08:58
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика




















PS. И тогда опять же можно утверждать, что и цена реального опциона это стоимость его репликации, потому что риск стоит денег.
В формуле БШ риск не стоит денег потому что у опциона есть покупатель и продавец — каждый из них несёт риск, но ничего за этот риск не получает.
В акциях, где эмитент не несёт рисков (у него закономерный убыток), а держатель — несёт, принято считать иначе. Но только потому, что одна из сторон явно отделяется от другой.
ну как же не стоит. Да каждый и покупатель и продавец несут риски, но это не значит, что они ничего не стоят. Покупатель покупает гамму и плати за это риском по тетте продавцу, а продавец получает тетту и платит за это покупателю риском по гамме.
Про акции, «где эмитент не несёт рисков (у него закономерный убыток), а держатель — несёт», честно говоря не понял, как можно это сравнивать.
Да, гамму и покупает — там больше нет ничего у опциона.
А про акции, поскольку вторая сторона сделки как-бы выбрасывается и остаются только покупатели, то для них рассчитывается риск (волатильность), коэффициент замещения риска доходностью (бетта) + индивидуальная склонность к риску… там целая теория. Но смысл именно такой — чем больше риски (волатильность), тем выше доходность... дальше…, не буду врать — теорию эффективно риска рынка я не поддерживаю.
да так и есть, можно это назвать гаммой, можно теттой.
Что касается акций, мне кажется вы пишите про эмитент/держатель акции, а думаете про ситуацию акция лонг/шорт. Мне думается, что это разные вещи, в случае держатель акции и эмитент — они в общем-то одно и тоже — они совладельцы бизнеса и по идее у них одинаковые риски.
если бы все было так просто. Попробуйте купить волатильность в чистом виде, у вас наверняка получится хорошенький замес из гаммы, тетты, волатильности и ещё чего нибудь, и все это будет напоминать волатильность очень отдаленно.
Фьючерсы на волатильность убираем в сторону, хотя даже они не являются волатильностью, хоть это и наиболее близкий к этому инструмент.
В одну сторону, предвидя Гамму, вы, быть может, и наберете гама-хедж, а когда заранее не известно куда цена пойдёт — увы
Алексей Борец, кто-то угадывает направление цены БА, кто-то угадывает настроение ММ в опционах. Конечно, если вы знаете, что завтра Аннушка прольёт масло и ММ неожиданно, придёт в голову гениальная мысль поднять страйк 22 200 в два раза, то лучше бы этот страйк прикупить заранее… «задельтохеджировать» так сказать.
Алексей Борец, вроде, недавно разбирали этот вопрос. Маркетос хеджирует по рынку, чтобы стабилизировать свой бук. И ему не важно, какая прибыль будет в итоге. Лишь бы посередине процесса к нему не прибегала биржа и не просила довнести соточку лямов.
А трейдер хеджирует «по уму» и терпит волатильность своего бука. Потому что в итоге всё равно добро победит зло.
В итоге все довольны.
Зачем тогда весь этот матан? )
Врач-бондиатОр, «весь этот матан» как раз за то, чтобы при минимальных рисках иметь приятный доход в несколько безрисковых ставок.
Тут вот один товарищ хвастается, что придумал 100% годовых безриска и считает, что этого мало.
> "Остаточный Гамма-Риск (теория) = 1.71, Эмпирический результат = 2.29"
Что-то пошло не так? =)
Но и разные дельтахеджеры работают чуть по разному.