SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. VadimTrade
Корреляция нефти и РТС
- 13 апреля 2016, 11:40
- |
Всем доброго утра!
Смотрю графики нефти(с площадки DAX) и нашего РТС! Поразительное совпадение важнейших узловых объемных точек, но при этом размах движений совсем разный!Вот пример совпадения узловых объемных точек!
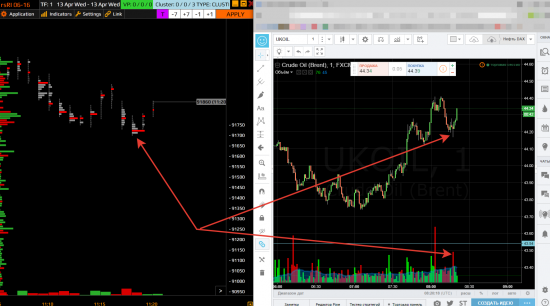
РТС часто повторяет волны на нефти, но их размер отличается достаточно сильно, поэтому при анализе двух графиков одновременно нужно быть очень внимательным. РТС повторяет нефть в направлении, но не конкретных волновых движениях!
Вот свежий пример, сравните углы наклона!
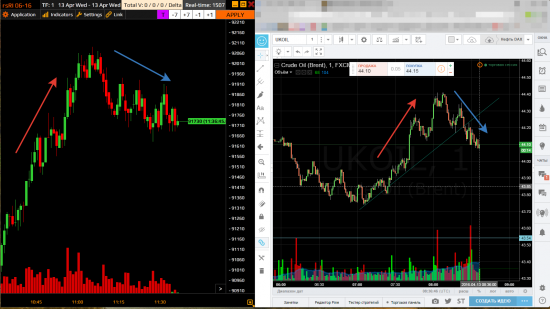
123 |
Читайте на SMART-LAB:

⚡️ Стартовало размещение 7-го выпуска облигаций ПСБ Финанс объемом 500 млн рублей
Напоминаем параметры: 🔘 Плавающий купон, ориентир ставки — КС ЦБ + 2%
🔘 Срок обращения — 3 года
🔘 Периодичность выплаты купона —...
11:45
теги блога VadimTrade
- bitcoin
- ED
- ri
- S&P500
- S&P500 фьючерс
- SB-Pro
- si
- sr
- US500
- yndx
- акции
- анализ
- анализ объема
- анализ рынка
- анализ фондового рынка
- бинарные опционы
- биржа
- биткоин
- биток
- ванюта
- вопрос
- втб
- выборы
- газпром
- геополитика
- герчик
- ГМК НорНикель
- гэп
- доллар
- Доллар рубль
- живой трейдинг
- золото
- инвестирование
- инвестиции
- интрадей
- капитализм
- кластерный анализ
- коронавирус
- кризис
- кризис 2020
- кризис2020
- криптовалюта
- кукл
- ложный пробой
- лукойл
- магнит
- манипуляции
- маркет мейкер
- мемы
- ммвб
- мобильный пост
- мосбиржа
- Московская Биржа
- начинающие трейдеры
- нефть
- обзор рынка
- обучение
- Объем
- объемный анализ
- околорынок
- опрос
- опционы
- оффтоп
- паттерн
- политика
- профиль рынка
- психология
- психология трейдинга
- рецензия на книгу
- ри
- роснефть
- ртс
- рубль
- рф
- рынок
- сбер
- сбербанк
- си
- смартлаб
- среднесрок
- статистика
- стоп лосс
- тантал
- торговля уровней
- торговые сигналы
- трейдер
- трейдинг
- тренд
- уровни
- форекс
- ФРС
- ФСК Россети
- фьючерс MIX
- фьючерс ртс
- ЦБ
- шум
- экономика
- экономика России
- юмор
- Яндекс






















То есть, в случае нестационарных рядов и нелинейных зависимостей она может вводить в заблуждение.
Если Вы не понимаете, при чем тут слова случайный и линейный, это не значит, что и другие не разбираются в вопросе.
Математические инструменты, как и любые другие, требуют не только знания названия и назначения, но и отработанного навыка использования. Прочтите из вики:
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанёс пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «увеличение количества пожарных приводит к увеличению причинённого ущерба», и тем более не будет успешной попытка минимизировать ущерб от пожаров путём ликвидации пожарных бригад. В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.