Число Пи

Мы привыкли к придыханию при упоминания числа Пи. Но что оно на самом деле? Тут возникает мой любимый вопрос: а может быть, все было наоборот? Если покопаться, то число пи просто производная. Вроде опциона. Как вообще его доказывали? Через вписанный круг:


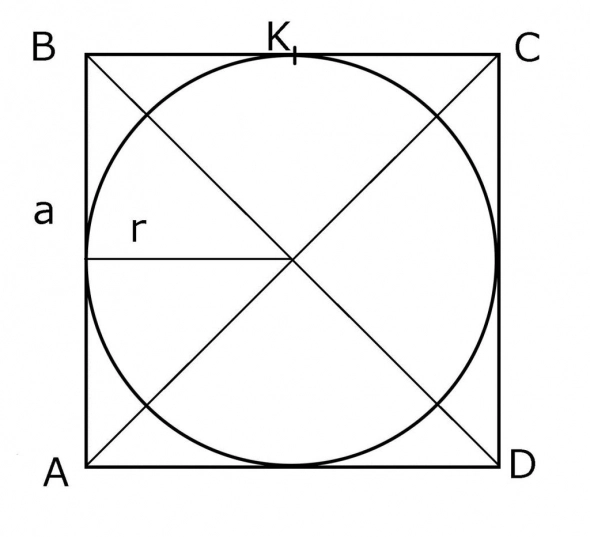
Площадь круга равна пи умн на радиус в квадрате, при радиусе в 1 это будет 3.14 умножить на 1 в квадрате. Площадь квадрата на рисунке равна квадрату стороны, а одна сторона равна 2 радиуса, т.е 4 радиуса в квадрате. Собственно Пи это антиразница между квадратом и кругом, т.е разница между 4 и 3.14 это и есть площадь квадрата, куда не вписался круг. Важно соответственно число 0.86радиуса в квадрате, это и есть разница между квадратом и кругом, а вовсе не освященное число пи.  Т.к. нагляднее представление в виде квадратов, то мы можем представить эту площадь остатка также в виде квадрата. Берем корень от 0.86 и получаем 0.92 радиуса, т.е.  0.46у. Т.е. при квадрате со стороной у разница между кругом в нем и квадратом у будет составлять квадрат со стороной 0.46у. Или 0.21 площади.
Это легко проверить, взяв квадрат со стороной 6, тогда его площадь 36, а площадь круга 3.14 на 9=28. Разница 7.7.  Корень 2.7. Делим на 6 (во столько была больше наша сторона). Получаем 0.46. 
Соответственно важны числа 0.46 линейно и  0.21  площади, а не сакральное число 3.14. Т.е. при выкройки круга из куска квадратной ткани у вас останется одна пятая обрезков от куска. При толпе в виде круга в квадратной комнате у вас будет свободна одна пятая площади. Вот что нам дают числа антипи, в то время как само пи, полностью производное, бесполезно.