Облигации: мифы и реальность. Часть 1. Невостребованная доходность.

Облигации -  простое и удобное средство для вложения своих сбережений. Если инвестора не устраивают ставки по банковским вкладам, он ищет аналогичные инструменты на фондовом рынке, и это, конечно, надежные облигации высокорейтинговых эмитентов: ОФЗ, субфедеральные, и другие бумаги, входящие в ломбардный список ЦБ. Инвестор перед покупкой обычно рассматривает такие параметры облигации как дата погашения, величина купона, цена и доходность. И если первые три, как правило, не вызывают вопросов, то последний параметр – доходность – имеет массу интерпретаций, что зачастую приводит к путанице и, как следствие, не всегда корректному сравнению различных облигаций. Всё дело в том, что и цены, и купоны непосредственно наблюдаются на рынке, а доходность – величина расчётная, т.е. выводимая из остальных параметров. Видов доходностей существует много: купонная, текущая, простая, эффективная к погашению, номинальная, к оферте и т.д. и т.п. Какую из них использовать каждый решает для себя, однако в финансовой литературе чаще всего используется так называемая YTM – доходность к погашению. Здесь и далее будем предполагать, что мы живем в мире плоских процентных ставок, т.е. кривые бескупонной доходности – просто константы. Также будем рассматривать только не содержащие опционов облигации с фиксированным купоном.

 Для n-летней облигации с ежегодным купоном C и номиналом H  YTM приравнивает ее цену P  к дисконтированному потоку будущих платежей:

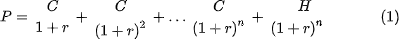
 К этой формуле так привыкли, что незаметно для всех она превратилась в формулу «нахождения цены облигации при известной требуемой доходности» Доходность в глазах финансовых менеджеров стала первичным фактором, а цена – производным. Иногда это приводит к недоразумениям. В реальности большинство облигаций на рынке выплачивают купоны не ежегодно, а чаще – раз в полгода, квартал, бывает даже ежемесячно. И сама формула может быть использована для любого числа выплат в год. В большинстве книг по инструментам с фиксированной доходностью ее видоизменяют так, что и выплаты, и доходность рассчитываются на один купонный период:

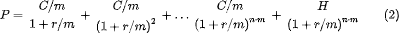
  Это общепринятый подход. Именно так, например, считает цену купонной облигации хорошо известная функция Excel ПС(ставка; кпер; плт; [бс]; [тип]). Этот метод хорош тем, что дисконтирует как купоны, так и номинал по одному и тому же правилу, а также позволяет элегантно перейти к непрерывному начислению процентов (устремив m  к ∞), используемому в литературе по финансовой инженерии.  

Однако, в широко известных онлайн-курсах от Высшей Школы Экономики проф. Н.Берзона (и в учебниках ВШЭ по финансам под его редакцией) можно встретить другую формулу для «вычисления цены купонной облигации с выплатой купонов несколько раз в год»:

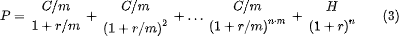
Здесь промежуточные выплаты дисконтируются согласно числу купонных периодов, но сам номинал – на годовой основе. Авторы объясняют это просто – облигация, которая платит купоны чаще одного раза в год, должна стоить дороже, чем аналогичная, но выплачивающая общую сумму купонов целиком, в конце года. И это чистая правда, ведь мы можем реинвестировать купоны и реализовать больший накопленный доход к концу срока погашения. Формула Берзона данному требованию отвечает. Кроме того, мы с удивлением обнаружим, что цена облигации, рассчитанная с помощью формулы (2), если подставить в нее то же значение r, что и в (1), будет не больше, а меньше (!), т.е. облигация с более частыми выплатами купонов парадоксально стоит дешевле. Так в чем тут подвох и почему формула Берзона, несмотря на всю ее привлекательность, все же неточна? Все дело в «доходностях к погашению» используемых в (1) и (2) Они на самом деле различны.

Рассмотрим такой пример:

Цена трёхлетней облигации номиналом 1000 руб. и ежегодным купоном 6% продается по номиналу. Сколько должна стоить такая облигация, если выплата купона будет происходить с периодичностью два раза в год, т.е. исходя из ставки 3% каждые полгода?  

   Заметим, что первая облигация торгуется с доходностью к погашению, которая равна купонной доходности, т.е. y₁=6% при годовом начислении процентов. Для определения требуемой доходности по второй облигации мы должны исходить из принципа отсутствия арбитражных возможностей или Закона Единой цены.Обе облигации должны давать одинаковый фактический накопленный доход при погашении.

Тогда легко показать, что требуемая доходность для купонного периода y_0.5 по второй облигации должна удовлетворять соотношению:

               
       Получим, что  y_0.5=2.96%, что не равно «ожидаемым»  3%.   Именно y_0.5  следует подставить вместо r/m в формулу (2) чтобы убедиться, что такая облигация будет стоить дороже номинала, а именно 1002.37 р. Таким образом, для облигации с лучшими характеристиками инвесторы просто потребуют более низкую доходность, r=5.92% (мы должны привести YTM к годовым величинам умножая на 2, чтобы получить требуемую доходность при полугодовом начислении процентов) Между тем, цена такой облигации,  найденная по формуле Берзона, будет меньше только что рассчитанной, что создает предпосылки для арбитража и получения неудовлетворительной оценки на экзамене CFA. С другой стороны, разница для низких процентных ставок и коротких горизонтов инвестирования совсем мала, так что формулу Берзона можно смело использовать для приближенных вычислений.

Однако сам по себе способ, используемый в формуле (2) не очень удобен. Для разных облигаций нужно вычислять свои доходности с m-периодным начислением, а это плодит сущности без острой необходимости. Неужели нет универсального подхода к оценке YTM? Он есть, и его можно найти у Дамодарана:

      

        где  – t_i фракции года, отвечающие времени получения купонов, т.е., например, для облигации  с полугодовыми купонами t₁ =0.5 , t₂ =1 ..   t_n =n. Всего получается  m*n  слагаемых.

При этом ставка дисконтирования рассчитывается на годовой основе, единый подход к дисконтированию денежных потоков как для купонов, так и для номинала сохраняется, полученная по формуле (4) цена совпадает с величиной, рассчитанной по формуле (2) при правильной подстановке в (2) доходности к погашению с m-периодным начислением. То есть, если использовать наш пример с 6% купонной облигацией, мы, подставляя в (4) те же 6% получим справедливую цену для облигации с полугодовыми купонами.   

Таким образом подходы (2) и (4) в целом эквивалентны и в этом нет ничего необычного, ведь все знакомы с различием между номинальными и эффективными ставками, когда имеют дело с получением банковского кредита. Более того, универсальность формулы (4) еще и в том, что с ее помощью можно дисконтировать и амортизируемые облигации, также она легко модифицируется для расчета цены облигации в межкупонный период.

 На сайте «Мосбиржи» https://www.moex.com/ru/bondization/calc для вычисления «эффективной доходности» используется именно формула (4) А вот под «номинальной доходностью» там понимают правильно найденную  доходность из формулы (2) Она будет всегда меньше либо равна эффективной.

А какая доходность используется в Quik, когда мы смотрим биржевой стакан? Конечно же, эффективная (4). Можно ли сравнивать облигации, используя эту доходность? Да, с определенными оговорками, можно. В исследуемом нами мире с плоскими и неизменными процентными ставками и невозможностью дефолта эмитента эффективная доходность – единственный критерий для принятия решения о покупке облигации. На рынке, конечно, трудно найти две облигации, отличающиеся только частотой купонных выплат. Но если инвестор их обнаружит, он не должен удивляться тому, что одна стоит дороже другой при одинаковой эффективной доходности в Quik. Причину этого мы и разъяснили выше.

Иногда на форумах бондовиков можно прочесть следующие мнения:

1)      Эффективная доходность не учитывает реинвестирование купонов. Это неправда, учитывает. Она ведь устроена таким образом, что предполагает реинвестирование купонов под эту же ставку.

2)      Я должен обязательно реинвестировать купон, чтобы получить всю-всю доходность. Здесь тонкость: не реинвестируемый, но потребляемый инвестором купон с точки зрения полезности равен реинвестированному. Я могу проесть его сейчас, а могу реинвестировать и дождаться, когда инфляция его обесценит. Это обычная проблема интертемпорального выбора.

3)      Эффективная доходность – это общая доходность, которую я получу, если буду удерживать облигацию до погашения и реинвестировать купоны. Это не так для мира изменяющихся во времени процентных ставок. В момент погашения облигации фактический накопленный доход может быть как выше, так и ниже рассчитанного при помощи YTM.  Подробнее этот вопрос будет рассмотрен в последующих статьях.