SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Toddler
Модель рынка как немарковского процесса. Часть 4.
- 13 июня 2020, 13:01
- |
Добрый день, господа!
До Грааля путь неблизкий и находится Он на 15-м уровне Инобытия в Тихом Доме.

Но, мы упрямо идем к Нему и никто нас не остановит. Не так ли?
Из прошлых исследований стало очевидно, что наилучшей средней, описывающей неслучайную часть рыночного процесса, является WMA с весами = абсолютным значениям приращений CLOSE(i)-CLOSE(i-1).
Кроме того, было показано, что стратегия «возврата к среднему» от границ дисперсионного канала для EURUSD с 01.01.20г. по 11.04.20г дала превосходные результаты на тестах.
Однако, все надо еще раз перепроверить, ведь есть глас сомнения типа: «Ты, папаша, протестировал только одну пару и тебе с ней просто повезло! А как на других? Работает?»
Ну, что ж — проверим метОду на паре AUDUSD с 01.03.20г. по 31.03.20г. в самый разгар коронавирусной паники.

Да, здесь ситуация хуже...
Результаты тестирования — проведено 3 сделки (+1/-2)

Общая прибыль: +1282 пункта по 5-знаку. Но, это не повод для веселья, ибо сделки №2 и №3 прошли с глубочайшими просадками и, при неверном манименеджменте, вполне могли буквально сокрушить депозит.
М-да...
Собственно, необходимо убедиться, что выбранная нами скользящая средняя WMA является лучшей среди общеизвестных.
Вспомним, что в немарковском уравнении
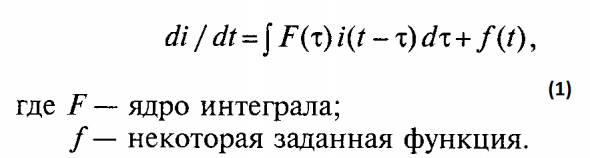
мы предположили, что функция f(t) характеризует поведение системы без учета памяти и, применительно к рынку, имеет смысл гауссовского «белого шума».
Однако, так ли это на самом деле? Критерий проверки будет самый простой. Определяем непараметрический эксцесс:

распределения цены относительно разных скользящих средних и, усредняя полученные значения узнаем — какое именно распределение у нас является приоритетным.
Итак, для пары AUDUSD имеем следующие усредненные значения эксцесса:
1. скользящая медиана. Mean kurtosis= 11.4644112821321
2. SMA. Mean kurtosis= 9.51264855980173
3. LWMA. Mean kurtosis=8.00403486129893
4. WMA с весами = ABS(CLOSE(i)-CLOSE(i-1)). Mean kurtosis=7.43182762465615
Для пары EURUSD:
1. скользящая медиана. Mean kurtosis= 9.32326943270398
2. SMA. Mean kurtosis= 7.3750433255463
3. LWMA. Mean kurtosis=5.85774061635379
4. WMA с весами = ABS(CLOSE(i)-CLOSE(i-1)). Mean kurtosis=6.20895651628314
Видим, что выбранная нами WMA, наряду с LWMA, является наилучшей. Но, все равно, вокруг них не образуется распределения Гаусса (kurtosis=3), а, в среднем, движется некое распределение очень близкое к распределению Лапласа (kurtosis=6).
Учитывая тот факт, что формула Эйнштейна-Смолуховского для среднеквадратичного отклонения частицы

выводилась для независимых приращений, сумма которых при большом объеме выборки должна принадлежать распределению Гаусса, можно сделать однозначный вывод, что данная формула на рынке нуждается в уточнении.
Что ж… Будем искать дальше… Путь в Инобытие к Граалю продолжается.
Всем — удачи!
Toddler.
До Грааля путь неблизкий и находится Он на 15-м уровне Инобытия в Тихом Доме.

Но, мы упрямо идем к Нему и никто нас не остановит. Не так ли?
Из прошлых исследований стало очевидно, что наилучшей средней, описывающей неслучайную часть рыночного процесса, является WMA с весами = абсолютным значениям приращений CLOSE(i)-CLOSE(i-1).
Кроме того, было показано, что стратегия «возврата к среднему» от границ дисперсионного канала для EURUSD с 01.01.20г. по 11.04.20г дала превосходные результаты на тестах.
Однако, все надо еще раз перепроверить, ведь есть глас сомнения типа: «Ты, папаша, протестировал только одну пару и тебе с ней просто повезло! А как на других? Работает?»
Ну, что ж — проверим метОду на паре AUDUSD с 01.03.20г. по 31.03.20г. в самый разгар коронавирусной паники.

Да, здесь ситуация хуже...
Результаты тестирования — проведено 3 сделки (+1/-2)

Общая прибыль: +1282 пункта по 5-знаку. Но, это не повод для веселья, ибо сделки №2 и №3 прошли с глубочайшими просадками и, при неверном манименеджменте, вполне могли буквально сокрушить депозит.
М-да...
Собственно, необходимо убедиться, что выбранная нами скользящая средняя WMA является лучшей среди общеизвестных.
Вспомним, что в немарковском уравнении
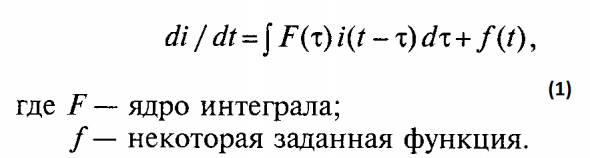
мы предположили, что функция f(t) характеризует поведение системы без учета памяти и, применительно к рынку, имеет смысл гауссовского «белого шума».
Однако, так ли это на самом деле? Критерий проверки будет самый простой. Определяем непараметрический эксцесс:

распределения цены относительно разных скользящих средних и, усредняя полученные значения узнаем — какое именно распределение у нас является приоритетным.
Итак, для пары AUDUSD имеем следующие усредненные значения эксцесса:
1. скользящая медиана. Mean kurtosis= 11.4644112821321
2. SMA. Mean kurtosis= 9.51264855980173
3. LWMA. Mean kurtosis=8.00403486129893
4. WMA с весами = ABS(CLOSE(i)-CLOSE(i-1)). Mean kurtosis=7.43182762465615
Для пары EURUSD:
1. скользящая медиана. Mean kurtosis= 9.32326943270398
2. SMA. Mean kurtosis= 7.3750433255463
3. LWMA. Mean kurtosis=5.85774061635379
4. WMA с весами = ABS(CLOSE(i)-CLOSE(i-1)). Mean kurtosis=6.20895651628314
Видим, что выбранная нами WMA, наряду с LWMA, является наилучшей. Но, все равно, вокруг них не образуется распределения Гаусса (kurtosis=3), а, в среднем, движется некое распределение очень близкое к распределению Лапласа (kurtosis=6).
Учитывая тот факт, что формула Эйнштейна-Смолуховского для среднеквадратичного отклонения частицы

выводилась для независимых приращений, сумма которых при большом объеме выборки должна принадлежать распределению Гаусса, можно сделать однозначный вывод, что данная формула на рынке нуждается в уточнении.
Что ж… Будем искать дальше… Путь в Инобытие к Граалю продолжается.
Всем — удачи!
Toddler.
5.2К |
Читайте на SMART-LAB:

USD/JPY у 160: рынок проверяет предел прочности иены
Четверг на валютном рынке снова стал днем нефти, в то время как макростатистика отошла на второй план. Рынок активно переоценивает не текущую...
18:36
Пять акций на весну 2026 года
Павел Гаврилов Российский рынок начал 2026 год в плюсе: Индекс МосБиржи прибавил почти 4%. Главные драйверы роста прежние: снижение ставки,...
18:40





















Если только то, что вышло, на выходе не сломалось вдребезги, без права и возможности восстановления (дерево, вывернутое с корнем или сломанное ураганом, уже не «вернется в канал»). Но этот вариант лишь исключение из правила, действующего всегда.
Поэтому надо всего лишь найти правильный канал. Что и пытается сделать ТС. ИМХО намеки на возможность успеха у него уже есть.
Пример вы привели просто шикарный, но сами его не понимаете.
Слово, кстати, из лексикона канатоходцев. )
Просто у каждого процесса свои границы баланса, что и пытается определять ТС. Касание границы баланса — триггер возврата.
Всё, больше мне добавить нечего, можете оставаться «при своих».
Вы пытаетесь объяснять совсем не то, что имеет ввиду автор.
Вы о визуальном геометрическом канале движения цены — это тоже метод, но метод совсем другой. Это из области графанализа.
В этом топике (и в моих объяснениях) речь совсем о другом.
Вот на этой картинке, какой канал правильный? Цена клоз, минутки, фьюч на Сбер.