Блог им. ipsnow
Как долго сохраняется распределение приращений цен?
- 02 июня 2020, 14:09
- |
Продолжаю экспериментировать с распределением ценовых приращений. Задался вопросом, насколько быстро меняется распределение в зависимости от:
1) размера выборки
2) соотношения «размер тестовой выборки / (размер основной + тестовой выборки)»
Техника простая — разбиваем серию минуток на перекрывающиеся интервалы, каждый интервал разбиваем на две части — основную выборку и тестовую, проверяем, отличается ли первая от второй. И так для каждой акции, размера целой выборки, размера тестовой выборки.
Перед отображением на графике результаты усредняем.
Факт изменения распределения определялся тестом Колмогорова-Смирнова.
Ниже — графики зависимости изменчивости распределения от размеров выборки (тестовой и совокупной)
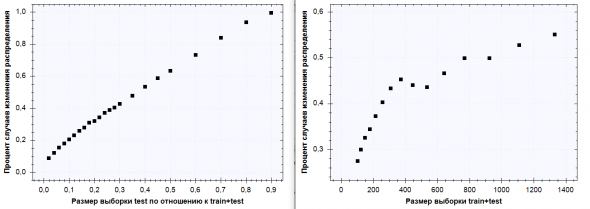
Замечу, что при небольших размерах выборки результаты на левой части графика становятся недостоверными (минимальный набор для теста Колмогорова-Смирнова ~ 30).
В целом результаты ожидаемы — чем меньше выборка, тем меньше вероятность того, что распределение последующей изменится.
Больший интерес здесь представляют конкретные числа — как долго и при каких размерах выборки распределение скорее сохранится, чем изменится?
Если убрать из результатов недостоверные тесты, получится, что реже всего распределение меняется при размере выборки в ~600 минут и размере тестовой в ~30 минут. Вероятность изменения при этом ~ 15% (на самом деле — это нижняя граница). Примерно, на это число и указывает впадина на втором графике. Подробности — в таблице:
| SamplesΞΞ | TestPartΞΞ | ProbabilityΞΞ |
|---|---|---|
| 534 | 0,06 | 0,152 |
| 641 | 0,06 | 0,198 |
| 770 | 0,06 | 0,21 |
| 179 | 0,22 | 0,233 |
| 371 | 0,14 | 0,252 |
| 179 | 0,26 | 0,277 |
| 179 | 0,28 | 0,301 |
| 1109 | 0,08 | 0,32 |
| 214 | 0,28 | 0,338 |
| 641 | 0,16 | 0,363 |
| 445 | 0,24 | 0,382 |
| 924 | 0,18 | 0,405 |
| 1109 | 0,16 | 0,425 |
| 124 | 0,45 | 0,441 |
| 641 | 0,28 | 0,456 |
| 1109 | 0,24 | 0,478 |
| 1331 | 0,24 | 0,499 |
| 257 | 0,4 | 0,527 |
| 1331 | 0,3 | 0,556 |
| 214 | 0,5 | 0,596 |
| 257 | 0,5 | 0,639 |
| 103 | 0,7 | 0,702 |
| 149 | 0,7 | 0,767 |
| 257 | 0,7 | 0,847 |
| 770 | 0,7 | 0,891 |
| 641 | 0,8 | 0,964 |
| 257 | 0,9 | 0,994 |
Вывод пока делаю такой: при построении статистических предсказательных методов на минутках ориентируемся на горизонт предсказаний в 30 мин, размер обучающей выборки — день. При этом частота изменения распределения, пусть и оцененная в нижней границе, значительно меньше 50%.






















MoscowTrades, не однозначно понял ваш вопрос, поэтому уточню условия эксперимента: бралось скользящее окно размером (base + test) и проверялось, отличается ли распределение test от base. Т.е. сравнивались не два соседних окна размерами (base + test)!