Дельта Хеджирование и Компрессия рисков

Каждый учебник предлагает нам простой и эффективный метод извлечения прибыли — репликация опциона при помощи фьючерса. При чем все, что для этого нужно — всего лишь «не думать и торговать по принципу: растёт — покупай, падает — продавай!».  Всё просто, понятно, бесспорно и… совершенно неверно.

Потому что «не думать» — в процессе погони за прибылью, — на самом деле, сложно. И если вам непонятно, зачем вообще нужны эти опционы, если они так легко реплицируются фьючерсами, то просто брать,  и «не думать», уже не получается. Не думать хорошо после того как вы уже хорошо  подумали, и думать второй раз — как минимум, лень. А с первого раза вообще мало чего получается. Особенно — не думать.


Так бы и закончилось моё дельта-хеджирование не начавшись, если бы оно не было столь модным. А то ещё всякое бывает — не задельта-хеджируешь, а потом скажут, что вот, дескать, «Пастернака не читал, но действия его уже осуждает». Нет, надо всё таки разок попробовать… А то в приличном обществе ещё и засмеют почём зря.


Ну и поскольку думать мозгами — это долго, а моделировать — вроде как побыстрее, то пошёл я за советом к бабе яге электронной, тем более она умнее — я-то всего лишь Кот, а она чай высокая технология… Дал ей случайный сигнал с волатильностью 1, дал проданных месячных стрэддлов с премией 10% годовых, фьючерсов для дельта хеджа с комиссиями по 0.1% и говорю — свари-ка мне милая, волшебное зелье дельта-хеджера! 

Та в ступу всё положила, пест в руку взяла, и как давай толочь, растирать! Через три дня и три ночи вынесла зелье… Говорит — если будешь по утру натираться, то все беды тебя стороной обходить будут, ни стрела не возьмёт, ни хворь, ни любовь окаянная.



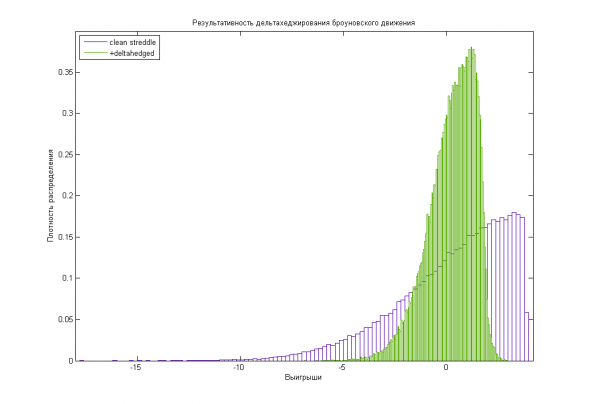
На тарелочке, да с каемочкой, мне картинку такую оставила. Говорит, хорошо будешь мазаться — в половину ли где риски снизятся, а доходность такой же останется, только чуть уйдет, несущественно, если фьючерсы брать не так дорого.