SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. SerSer
Альтернатива стандартному Болинджеру - Болинджер через линейную регрессию
- 09 июля 2016, 23:04
- |
Добрый вечер.
При одних и тех же периодах — намного информативней и интересней...
При одних и тех же периодах — намного информативней и интересней...

Settings =
{
Name = "xBollinger_LinReg",
period = 40,
deviation=2,
line=
{
{
Name = "xBollinger_LinReg",
Color = RGB(0, 0, 255),
Type = TYPE_LINE,
Width = 2
},
{
Name = "xBollinger_LinReg",
Color = RGB(192, 0, 0),
Type = TYPE_LINE,
Width = 2
},
{
Name = "xBollinger_LinReg",
Color = RGB(0, 128, 0),
Type = TYPE_LINE,
Width = 6
}
}
}
function c_FF()
local AMA={}
local CC={}
return function(ind, _p,_ddd)
local period = _p
local index = ind
local vol = 0
local sigma = 0
local sigma2 = 0
local aav = 0
local bb = 0
local ZZZ = 0
if index == 1 then
AMA={}
CC={}
CC[index]=(C(index)+H(index)+L(index))/3
AMA[index]=(C(index)+O(index))/2
return nil
end
------------------------------
AMA[index]=AMA[index-1]
CC[index]=(C(index)+H(index)+L(index))/3
if index < (_p) then return nil end
period =_p
if index < period then period = index end
---------------
sigma=0
sigma2=0
aav=0
ZZZ=0
for i = 0, period-1 do
ZZZ=CC[index+i-period+1]
aav=aav+ZZZ
sigma=sigma+ZZZ*(-(period-1)/2+i)
sigma2=sigma2+(-(period-1)/2+i)^2
end
bb=sigma/sigma2
aav=aav/period
AMA[index]=aav+bb*((period-1)/2)
sigma=0
sigma2=0
sigma3 = 0
for i = 0, period-1 do
ZZZ=CC[index+i-period+1]
sigma2=aav+bb*(-(period-1)/2+i)
sigma=sigma+(ZZZ-sigma2)^2
end
sigma=(sigma/period)^(1/2)
return AMA[index]-sigma*_ddd,AMA[index]+sigma*_ddd, AMA[index]
end
end
function Init()
myFF = c_FF()
return 3
end
function OnCalculate(index)
return myFF(index, Settings.period,Settings.deviation)
end
350 |
Читайте на SMART-LAB:

Запускаем новый формат на Смарт-Лабе
Привет! На связи Сергей Алексеев (основатель Лайв Инвестинг Групп) и Иван Кондратенко (трейдер и ведущий Трейдер ТВ).
Мы временно...
10:57

📄 Ресейл Инвест получил право проводить закрытые размещения акций
Банк России согласовал правила инвестиционной платформы Ресейл Инвест. Платформа сможет осуществлять деятельность в соответствии с...
13:00
теги блога Маркин Павел
- Brent
- EUR USD
- Gold
- indicator
- LUA
- micex
- MOEX
- qlua
- quick
- quik
- ri
- rts
- S&P
- si
- treemapping
- usd
- акции
- алгоритм
- алготрейдинг
- аномалия
- АСВ
- банки
- Башнефть
- безграмотность
- биржа
- брокеры
- бюджет
- волатильность
- ВТБ
- Газпром
- голодовка
- дивиденды
- доллар
- звезда
- золото
- инвестор
- Индекс ММВБ
- Индикакаторы
- индикатор
- Инициативы ЦБ
- Карта рынка
- квик
- корреляция
- лидеры падения
- лидеры роста
- лидеры роста и падения ММВБ
- ликвидность
- ЛЧИ 2016
- Минфин
- ММВБ
- Набиуллина
- нетипичные объемы
- нефть
- НЛМК
- новость
- Облигации
- ограничения
- опек+
- опрос
- Опционы
- офз
- оффтоп
- приватизация
- Путин
- Распадская
- рейтинг
- риски
- робоадвайзинг
- роботы
- роснефть
- Россети
- Россия
- рост
- Ростелеком
- ртс
- рубль
- рынки
- рынок
- сарказм
- сбербанк
- Сечин
- смартлаб
- СОФТ
- срочный рынок
- статистика
- тарифы
- тарифы биржи
- тепловая карта
- технический анализ
- торговые сигналы
- трейдинг
- тренд
- Турция
- Улюкаев
- ФОРТС
- ФСК Россети
- ЦБ
- ЦБ России
- шорт
- юмор




















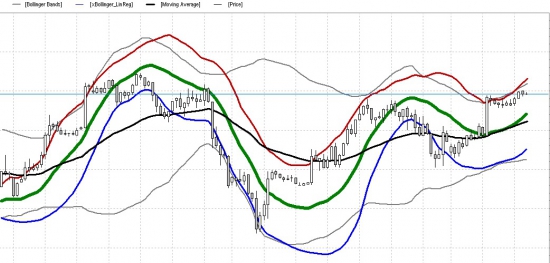
черный/серый — стандартный болинджер квика,
красный/зеленый/синий — альтернативный индикатор болинджера
обычные средние (MA) отражают изменение тренда очень и очень постфактум, в отличии от линейной регрессии.
А проще (если у Вас квик) возьмите индикатор и протестируйте.
Причем тут опережение, когда сам боллинджер самодостаточен и показывает как раз то, что нужно — классическое стдв.
Среднее значение — является вырожденным частным случаем уравненения линейного тренда y=a+bx при b=0 ==> y=a. И Болинджер отражает отклонение от среднего значения, при предположении, что динамический ряд значений статичен и не имеет трендовой направленности.
В предлагаемом варианте Болинджера, отражается отклонение цены не от статичного значения вырожденной функции, а от направления тренда и в рамках его системы координат.
И извините, что путаю Ваши знания с пальцем.