Пограничный контроль

В последнее время отечественный рынок переживает настоящий бум облигаций с плавающей процентной ставкой.  Некоторые аспекты ценообразования и риска простых   флоатеров  изложены в этой статье.

Как и обычные купонные  облигации, флоатеры могут содержать различные встроенные опционы.  Развиваемый в нашем цикле публикаций подход  разбиения денежного потока  на компоненты с хорошо изученными свойствами помогает оценивать сложные инструменты с фиксированным доходом.

 Флоатеры с ограничениями на величину ставки купона

 Эмитент облигаций с плавающим  купоном несет дополнительные расходы, если  процентные ставки устойчиво растут. Покупатель, в свою очередь, не заинтересован в том, чтобы ставки оказались слишком низкими. Для защиты эмитента или владельца  облигаций от неблагоприятной рыночной конъюнктуры, в формулу расчета купонов вносят дополнительные условия.

Например,  владелец флоатера с нижней границей ставки купона K  получает выплаты по плавающей ставке L, если  L >  K. В тех же случаях, когда L  ≤ K, купон будет рассчитан исходя из фиксированной ставки K:

Иными словами, эти бумаги обеспечивают минимальный платеж, если ставки остаются ниже предела, но не препятствуют получению более высокой доходности. 

 Соответственно, флоатеры с верхней границей ставки купона выплачивают владельцу плавающую ставку до определенного уровня, после чего ставка ограничивается. Если плавающая ставка превышает установленный предел, инвестор получает доход, рассчитанный по фиксированной, а не плавающей ставке:

Как найти справедливую цену этих облигаций?

Рассмотрим сначала флоатер с нижней границей купона (в англоязычной литературе он называется floored FRN) Разобьем его денежный поток  на две составляющих:

1.   Все выплаты по плавающей ставке Lₖ₋₁,ₖ, поступающие в моменты tₖ. Величина каждой из них  F·Δtₖ· Lₖ₋₁,ₖ   Кроме того, учтем погашение суммы номинала в конце срока. 
2.  Серия “возмещений”, каждая размером  F·Δtₖ· max[K — Lₖ₋₁,ₖ, 0].  Выплата “возмещения” в момент tₖ происходит,  если плавающая ставка Lₖ₋₁,ₖ   <  K 

Такое разбиение вполне допустимо, поскольку имеет место равенство:

                             max[L, K] = L + max[K — L, 0]

Свойства денежного потока, определяемого в [1], нам уже известны  — это простой флоатер без спреда, и его цена равна номиналу  F сразу после выплаты очередного купона 

Условный денежный поток в [2] соответствует выплатам по  производному финансовому инструменту “флор” (floor) Он представляет собой набор опционов “пут” на процентные ставки (так называемых “флорлетов”  — floorlets) с датами экспирации, соответствующими временам поступления платежей, и единым страйком  —  фиксированной ставкой K.   Покупатель дериватива “флор” гарантирует себе минимальную ставку K в каждом периоде. Если рыночные ставки в каком-то из периодов опустятся ниже K, продавец ПФИ выплатит покупателю разницу между рыночной и гарантированной процентными ставками.

Формулу цены флоатера с нижней границей купона легко запомнить с помощью мнемонического правила сложения стоимостей его элементов:

          “Floored FRN” = “Face Value” +  “Floor”

Аналогичные рассуждения можно провести и для  флоатера с верхней границей купона (capped FRN) Мы снова  разобьем денежный поток на две части, используя соотношение:

                                   min[L, K] = L — max[L — K, 0]

Первая часть соответствует простому флоатеру, а вторая — условному денежному потоку по  ПФИ “кэп” (cap) Знак “минус” в выражении перед max[] означает, что дериватив продается владельцем флоатера эмитенту.  В отличие от дериватива “флор”, «кэп» – это набор опционов  “колл” на процентные ставки, называемых "кэплетами" (caplets). Продавец дериватива “кэп” компенсирует покупателю превышение  установленного уровня рыночной ставки.  Условие Lₖ₋₁,ₖ — K > 0 проверяется в начале каждого купонного периода (Напомним, что  ставка Lₖ₋₁,ₖ устанавливается в начале купонного периода, т.е. в момент tₖ₋₁,   а  купон выплачивается  в момент tₖ.) 

Мнемоническое правило для вычисления цены флоатера с верхней границей купона:

“Capped FRN” = “Face Value”  —  “Cap”

Поясним чуть подробнее упомянутую выше куплю-продажу деривативов. Продавец опциона/серии опционов получает за него сумму, называемую премией. Когда мы говорим, что покупатель облигации “capped FRN”  продает “кэп”, то подразумеваем получение им премии от эмитента в виде разницы цен между простым флоатером и “capped FRN”.  “Ограниченный сверху”  флоатер выгоден эмитенту и он согласен заплатить премию владельцу бумаги, а значит “capped FRN” будет дешевле простого флоатера. В случае с “floored FRN” уже эмитент потребует вознаграждение от покупателя (ведь он несет расходы при возмещении разницы ставок), поэтому такой флоатер дороже обычного  на размер премии за “флор”.

Оценка деривативов “флор” и  “кэп” зависит от используемой модели и может быть рассчитана аналитически либо численными методами. Рассмотрим случай, когда облигации не имеют срока погашения (консоли, “вечные облигации”)  и непрерывно, т.е  в каждый момент времени, выплачивают купоны. Пусть динамика плавающей ставки описывается разновидностью модели CIR без возврата к среднему.

 На рис. ниже изображен пример  реализации этого стохастического процесса.   Предельная ставка 7% делит весь график на два участка определения ставки купона для флоатеров с нижней и верхней границей.

Стоимость флоатеров в этой модели может быть найдена аналитически. Вот как выглядит качественная зависимость цен облигаций различного типа от отношения L/K (L  — плавающая, K  — граничная ставки), если не учитывать премию за риск:

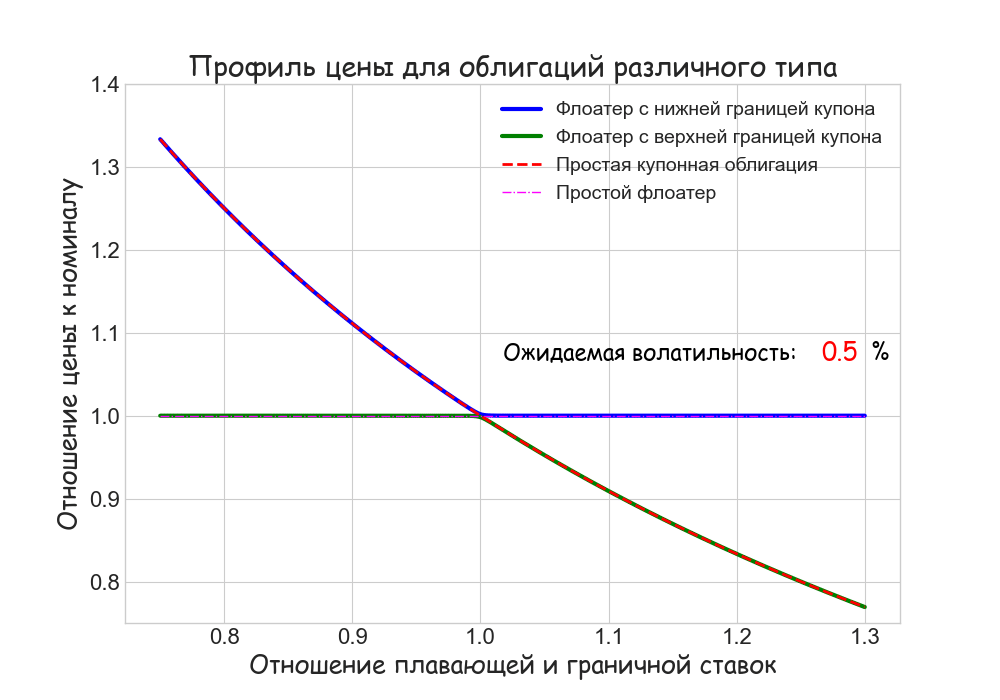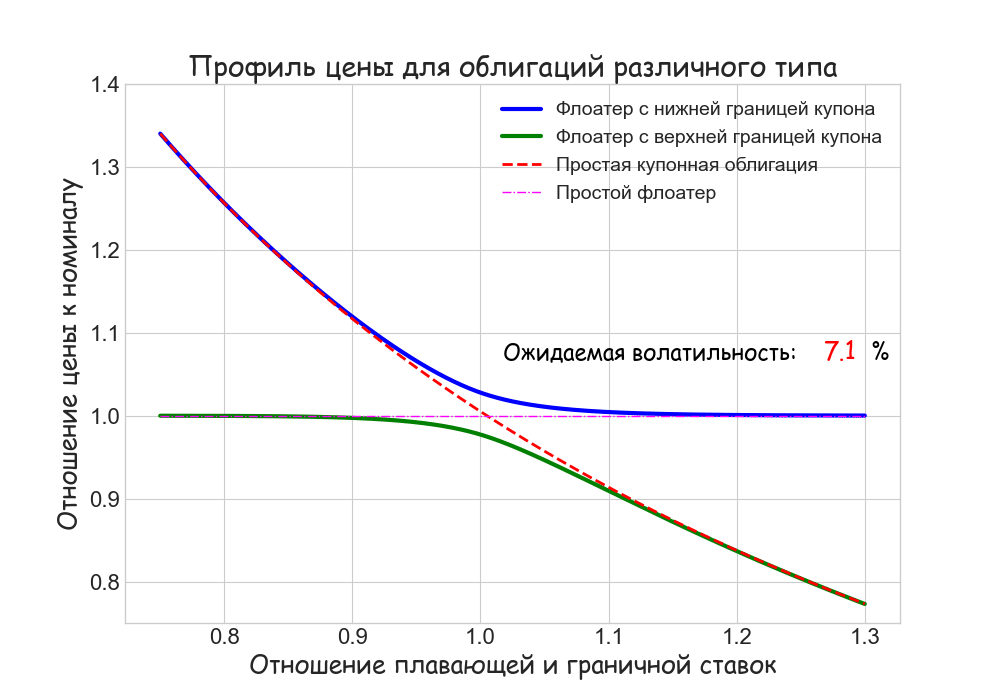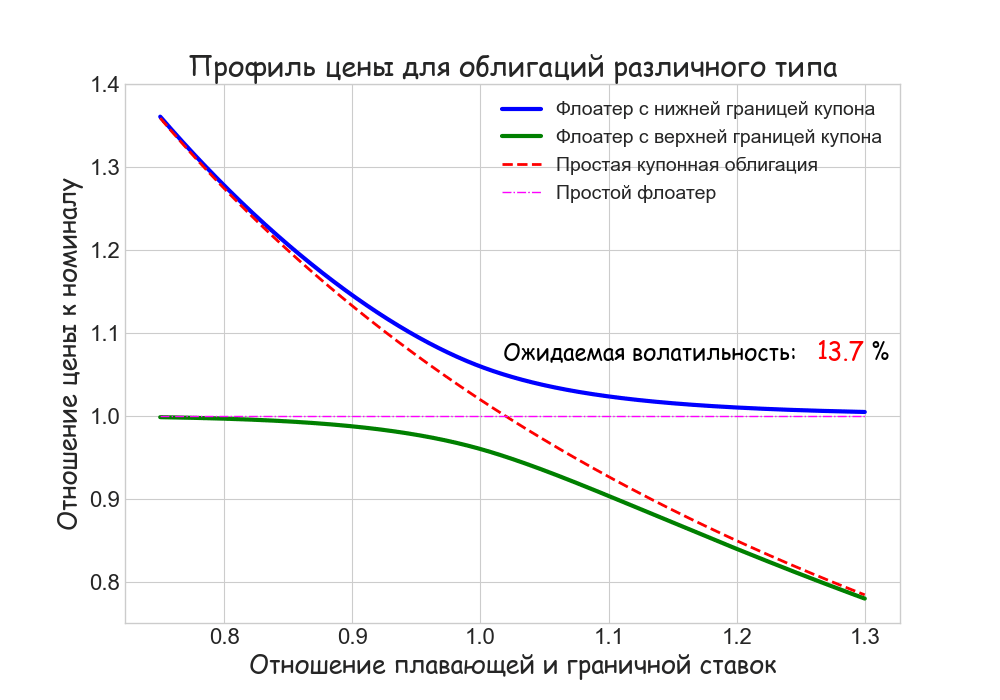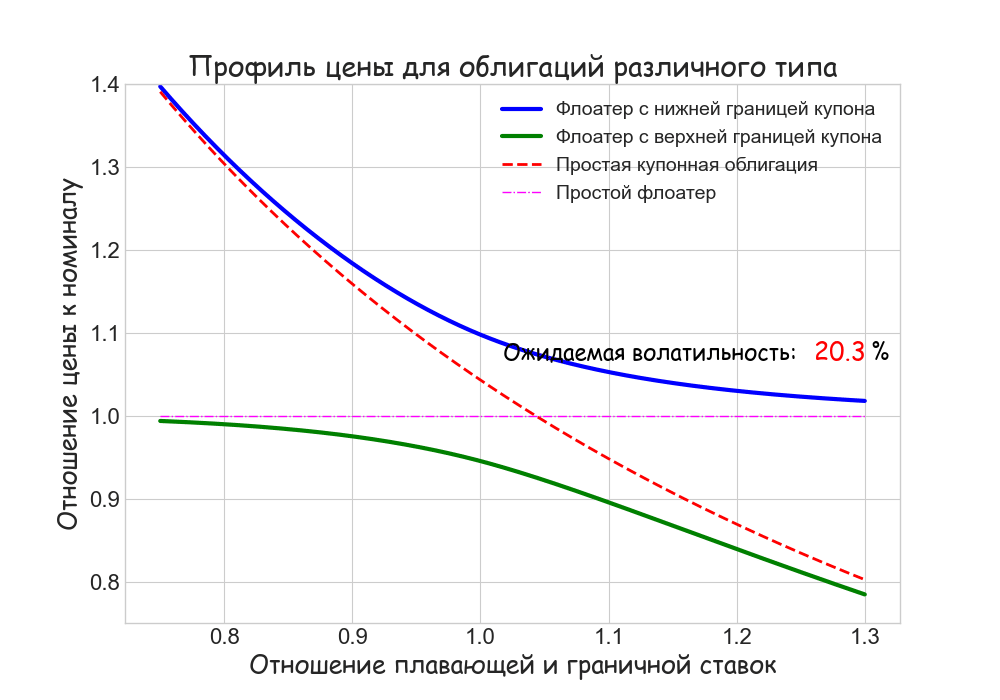
Для сравнения приводятся графики цен обычного флоатера и простой облигации с купонной доходностью  K. 

Стоимость простого  флоатера при непрерывном начислении и выплате процентов всегда равна номиналу. Вечная купонная облигация оценивается как перпетуитет, но из-за стохастического характера динамики ставок ее цена также зависит от величины ожидаемой волатильности: P = F/[a·(L/K)], где a  = √(1 — σ²) и  σ  — ожидаемая волатильность. Поэтому, если волатильность растет и инвесторы не требуют дополнительную премию за риск, цена вечной облигации увеличивается (мы обсуждали это в предыдущих статьях, когда говорили про склонность к выпуклости и ее влияние  на цены длинных облигаций)  

В зависимости от соотношения ставок L  и  K  флоатеры c ограничениями на ставку купона ведут себя противоположным образом. Если  плавающие ставки (по сравнению с граничной) низкие, а волатильность умеренная, то  floored FRN стоит почти столько же как простая купонная облигация, а capped FRN  — как простой флоатер. Если плавающие ставки высоки, картина меняется на противоположную.  Это объясняется обратной связью стоимости деривативов “кэп” и “флор” от L/K.  Ценность “флор” растет при снижении рыночных ставок, а “кэп”   — уменьшается. С ростом ставок все происходит наоборот. 

При прочих равных условиях с увеличением волатильности стоимость деривативов “кэп” и “флор” возрастает. В этом случае цена capped FRN снижается, так как “кэп” входит в формулу расчета со знаком “минус”.

На анимированном графике ниже указана зависимость ценового риска от отношения L/K.  Фактически это дюрация в безразмерных величинах, т.к. относительный риск ρ =   —K[dP/P] =  K·D:

Ценовой риск флоатеров  не превышает дюрацию вечной облигации, 1/L. (красная прерывистая линия) Переходная область, где L ≈ K, при малых значениях волатильности отличается  крутым наклоном кривой риска. Деривативы «кэп» и «флор» в этом случае находятся в состоянии “возле денег” (at the money, ATM), в котором влияние волатильности носит определяющий характер: чем она выше, тем более гладкой становится кривая риска.

 Пример облигации с встроенным деривативом «флор»

В январе 2024 г. «Альфа-Банк» разместил трехлетние облигации с квартальными выплатами. Формула расчета процентной ставки со второго по двенадцатый купонный периоды такова: 

Сi = max (25,90% — R; 12,90%),

где:

Cj – размер процентной ставки i-го купона, в процентах годовых;

i – порядковый номер купонного периода, (i=2, 3,…, 12);

max – наибольшее из указанных в скобках значений;

R – среднее значение Ключевой ставки Банка России, рассчитываемое по формуле:

R = (R-2 + R-1 …+Rn)/T,

где:

R-2 — Ключевая ставка Банка России, действующая по состоянию на 2 (Второй) календарный день, предшествующий дате начала i-го купонного периода;

R-1+…+Rn — Ключевая ставка Банка России, действующая по состоянию на каждый календарный день, начиная с 1 (Первого) календарного дня, предшествующего дате начала i-го купонного периода (R-1) и заканчивая включительно 3 (Третьим) календарным днем, предшествующим дате окончания i-го купонного периода (Rn);

T – общее количество календарных дней начиная с даты расчета R-2 до даты расчета Rn.

Методика определения величины  R позволяет считать ее  релевантной плавающей ставкой, так как

1. Усредняются текущие, а не прошлые значения ключевой ставки ЦБ.

2. Средние значения ключевой ставки ЦБ и RUONIA хорошо коррелируют:

Вместе с тем волатильность ключевой ставки значительно ниже, чем у RUONIA, что необходимо учитывать при моделировании купонных выплат. 

Денежный поток облигации АЛЬФА-БАНК Б1Р11 можно разбить на две части, используя соотношение: 

      Max (25,90% — R; 12,90%) = 12.9% + Max(13%  — R; 0)

Применяя тот же подход, что и в предыдущем топике,   легко записать мнемоническое правило:

 “A-Bond” = “Simple Bond” +  “Floor”

Таким образом, обл. АЛЬФА-БАНК Б1Р11  содержит встроенный ПФИ “флор”, а ее общая стоимость слагается из стоимости простой облигации  с купонной доходностью 12.9% и  стоимости “флора” с граничной ставкой 13% годовых.

Для вычисления цены простой облигации потребуется оценка Z-спреда.  У торгуемых на рынке бумаг Альфа-банка с дюрацией выше 2-х лет года он сравнительно невелик  —  60-90 б. п., что отражает высокий кредитный рейтинг эмитента. По самому новому трехлетнему  выпуску, Альфа-Банк-002Р-26-боб, финальный ориентир ставки  купона установлен в размере  13.8% годовых, и соответствует доходности к погашению 14.53% годовых. Z-спред в этом случае может составить 120-130 б. п. 

При значениях Z-спреда в диапазоне  70-120 б. п. справедливая цена “Simple Bond”  находится  в пределах от 99% до 100% от номинала, на дату оценки 15.02.2024. В таблице ниже представлен расчет стоимости  “Simple Bond” для величины Z-спреда в 100 б. п.

Дать справедливую оценку ПФИ “флор” сложнее, необходимо выбрать случайный процесс, описывающий динамику процентных ставок.  Например, в дискретном аналоге модели Блэка – Дермана – Тоя (BDT ) для дисконтирования денежных потоков  используется биномиальная решетка коротких ставок. Модель калибруется по текущим значениям КБД  при заданной структуре  волатильности и дает хорошие  результаты для простых купонных облигаций. Кроме того, понадобится прогноз динамики усредненного значения ключевой ставки ЦБ, исходя из которой должны  определяться величины условных выплат [рассчитанные по условию Max(13%  — R; 0)]

Расчет  с учетом Z-спреда 100 б.п. и  ожидаемым уровнем волатильности  ставки дисконтирования в 50% (это достаточно много) дает оценку дериватива “флор” в 4.5% от номинала, если же принять волатильность равной  10%   оценка “флор”” снижается до 1.5%. Консервативная оценка текущей стоимости облигации АЛЬФА-БАНК Б1Р11 находится в диапазоне  101%-102%

Сделок по бумагам пока нет, так же как и не видно оферов в стакане. Одно время мелькал единичный лот на покупку в размере 105% от номинала, но это могло быть котировочной игрой неизвестных манипуляторов.