Портфельная оптимизация как бустинг на «слабых» моделях-3

Устойчивые долгосрочные модели


В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения»  (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.

В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.

В то же время Boost часть композиции, состоящая преимущественно из динамических и AR моделей сохранилась в виде надстроечной системы кредитного скоринга, используемой преимущественно в краткосрочных («активных»)  стратегиях.

Прим. Простейший бинарный кредитный скоринг это: фильтр тренда, фильтр пилы, фильтр плечей и подобные фильтры. 

В долгосрочных стратегиях, на рассматриваемых интервалах более полугода и сроках инвестирования более 3-х месяцев (особенно с учётом временного рассеяния сделок), Boost часть полностью теряет свою адекватность. Исключением, разве что, могут оставаться Фурье-фильтры, уберегающие базовую модель от ошибок нахождения трендов внутри бокового движения. 

Тем не менее, долгосрочные стратегии, в результате пониженных требований к ликвидности, представляют собой отдельный класс задач, решаемый управляющими крупных взаимных фондов и поэтому заслуживают отдельного рассмотрения.
 

Для того чтобы оценить применимость модели Марковица в области управления крупным капиталом мы провели серию тестов полученной универсальной событийной модели (без скоринг-фильтров) на российском и американском рынке. Цель – получение дельты к рынку +50% — +100% при улучшении показателя Шарпа.



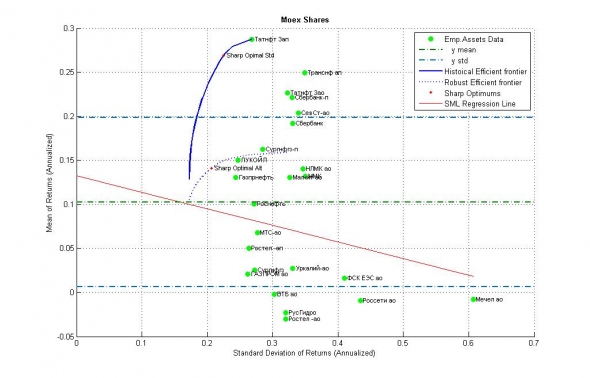
Рис. 13. Изображение распределения активов на российском фондовом рынке внутри исследуемого интервала (In Sample).

В предположении, что мы можем отделить хороший актив, с потенциалом роста, от плохого актива математическое ожидание нашего инвестирования должно составить около:

E[portfolio] = E[market] + 0.8*Std[market] или около 10%+8% = 18% годовых.

(Следствие нормального закона распределения)

Эта же оценка, как ни странно, находится на эффективной робастной границе доходностей, полученной в предположении строгой отраслевой сегментации активов или их иной кластеризации.

 


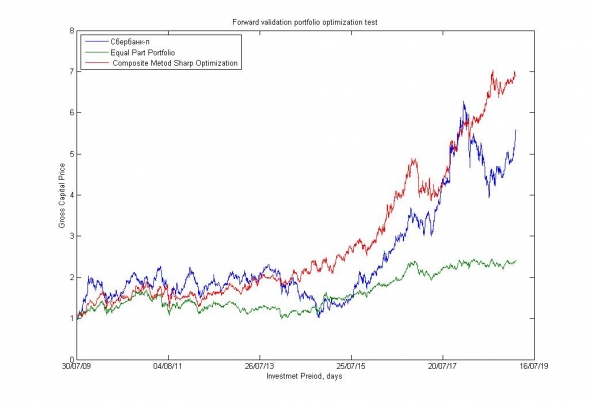
Рис.13. Результаты тестирования стратегии оптимального портфельного инвестирования по Марковицу с ограничением оборота 1.7%  на фондовом рынке ММВБ.

Результаты испытаний показывают, что  ограничение оборота портфеля ниже 1.5%-2% в день начинают достаточно сильно влиять на результаты стратегии. До этих уровней ограничений, долгосрочные портфели формируются более-менее свободно.

К сожалению, с учётом ликвидности активов не входящих в топ-10 (около 100 млн. руб./день) предел активного управления капиталом наступает уже на уровне около 1.5 млрд. рублей (25 млн. долл. США) – свыше этой суммы уже неминуемо начинается индексное инвестирование, привязанное к ликвидности каждой бумаги.

Прим. В качестве оценки доступной для инвестора ликвидности мы взяли 3% от полной дневной ликвидности ценной бумаги.

В лучшем случае, для активных стратегий с капиталом более 1.5 млрд. рублей, остаётся только активное управление в 10 наиболее ликвидных бумагах, поднимающее оценку предела управляемого капитала до 7-15 млрд. рублей (250 млн. долл. США).

 
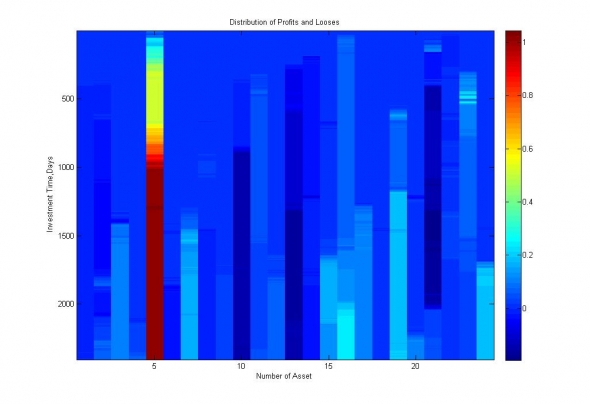
Рис. 14. Тепловая карта финансовых результатов долгосрочного инвестирования в российский рынок ценных бумаг  по активам.

Изображение демонстрирует приблизительно 50% использование рынка ценных бумаг долгосрочным портфелем.

 
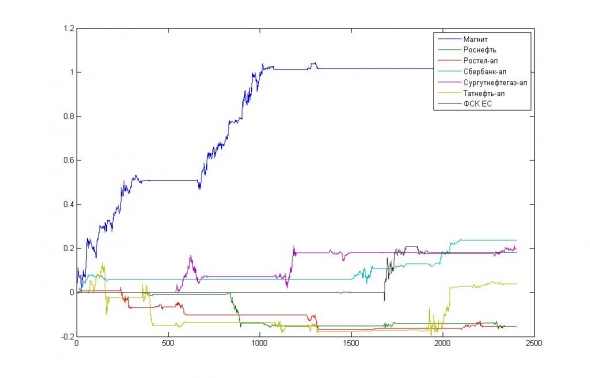
Рис. 15. Основные прибыли и убытки во времени.

 


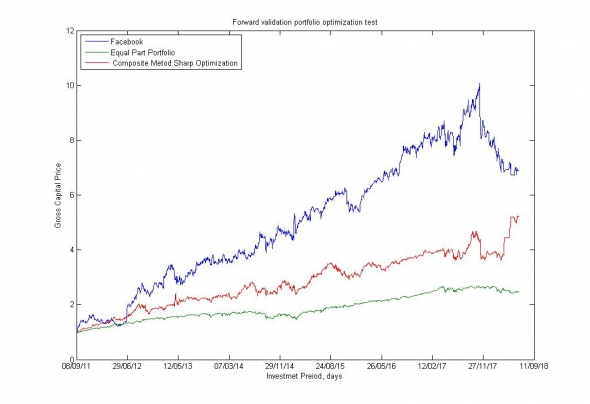
Рис.16. Результаты испытаний полностью идентичной системы на американском фондовом рынке.

 
Рис.17. Итоговая таблица результатов.

Таким образом, нам удалось достичь требуемой теоретической дельты к рынку (+100%) на долгосрочных системах портфельной оптимизации, не сильно требовательных к ликвидности.  К сожалению, предел свободной ликвидности (для торговли без ограничений) на рынках даже для этого типа стратегий начинается очень рано — на уровнях около 1.5 млрд. рублей и 3 млрд. долл. соответственно.