SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Торговые сигналы!
Читайте на SMART-LAB:

Скидка 15% на нашу аналитику — только 72 часа!
Увеличь доходность своего портфеля с профессиональной командой аналитиков. Наши идеи уже принесли клиентам прибыль с начала года. Ты мог...
21 февраля 2026, 10:04

Актуализация взгляда на акции Северстали: пришло ли время покупать?
Здравствуйте! Хочу поделиться актуальным видением на бизнес Северстали и стоимость акций в условиях текущей неблагоприятной рыночной конъюнктуры....
01:57





















Хочешь написать топик по данной теме пиши будут коменты.
Умничать не надо. Куча народу здесь кто торговать Америку в разы дольше чем ты.
Пиндосы, не пиндосы… а шороху на пауке тогда навели.
Смысл в ентом есть, о чем, собстнна, хотел и пообщаться
Не ресурс — а говно, Тима!
Полное сообщение было такое:
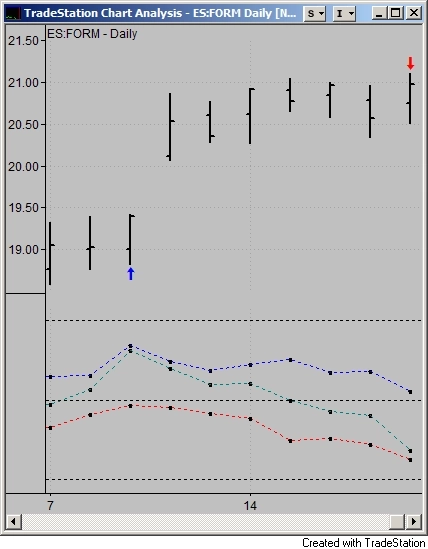
Подобрал достаточно красивую картинку с сигналом на закрытии пятницы (синяя линия это «заинтересованность» к покупкам, красная — к продажам), на этом пока завершаю свой рассказ. Всех с наступающими и всего наилучшего
--------------------
Anticipate crowd's thoughts, trade its nightmare.
Прошла двадцатка лет всё-таки.
А то писали-писали топикстартеры на пауке, КПД от их информации тогда не было, что видно по содержанию всего форума. Хотя позиционировали они себя «посвященными».
Мне лично более зашел форум Атамана. Но это дело вкуса. И доступа к старым форумам.
Публицист. Вот его стратегия: www.forexfactory.com/thread/503435-long-wind над которой ломали голову долгое время
Про бифуркацию и возможность ее рассчитать заранее:
Термин бифуркация (букв. раздвоение) употребляется для обозначения качественной перестройки, изменения той или иной картины ѕ в нашем случае фазового портрета обыкновенного дифференциального уравнения при изменении входящего в это уравнение параметра. Простейшим примером может служить, например, изменение фазового портрета системы.
При прохождении параметра e через 0: при e < 0 фазовый портрет представляет собой узел, а при e > 0 ѕ седло.
Из всего необъятного множества различных бифуркаций мы опишем лишь несколько простейших типов. Поскольку теория бифуркации требует довольно развитой техники, мы как правило не описываем даже идей доказательств.
Начнем с описания локальных бифуркаций состояния равновесия динамической системы. Мы будем рассматривать автономную системы обыкновенных дифференциальных уравнений с параметром вида
xў = f(x, e), (1)
предполагая, что f: Rn, R ® Rn ѕ непрерывно дифференцируемая функция. Допустим, что уравнение (1) при e = 0 имеет стационарную точку x0: f(x0,0) = 0. Будем говорить, что точка e = 0 является точкой локальной бифуркации динамической системы (1) со стационарной точкой x0, если найдутся сколь угодно малые значения e, при которых динамическая система (1) в окрестности точки x0 не является локально топологически эквивалентной системе, отвечающей нулевому значению параметра.
Допустим, что у матрицы [(f(x, e))/(x)]|(x, e) = (x0,0) нет собственных значений на мнимой оси. Тогда, в частности, в силу теоремы о неявной функции уравнение
f(x, e) = 0 (2)
локально однозначно определяет x через e, т. е. в малой окрестности точки x0 для любого достаточно малого e найдется единственное решение xe уравнения (2), или, что то же, стационарная точка уравнения (1). Кроме того, поскольку решение xe и матрица A(e) = [(f(x, e))/(x)]|(x, e) = (x0,0), а следовательно и ее собственные значения, непрерывно зависят от e, при малых e числа n-[A(e)] собственных значений этой матрицы с отрицательной вещественной частью и число n+[A(e)] собственных значений этой матрицы с положительной вещественной частью не зависят от e.
Поэтому из теоремы Гробмана ѕ Хартмана и теоремы о топологической эквивалентности линейных систем вытекает, что при малых e все динамические системы (1) в окрестности своих стационарных точек xe локально топологически эквивалентны, и следовательно, e = 0 не является точкой бифуркации.
Таким образом, чтобы точка e = 0 была точкой локальной бифуркации динамической системы (1) со стационарной точкой x0 необходимо, чтобы матрица A(0) имела хотя бы одно собственное значение на мнимой оси.
Мы рассмотрим только два случая выполнения этого условия: когда A(0) имеет простое нулевое собственное значение и когда A(0) имеет пару простых комплексно сопряженных мнимых собственных значений.
Для иллюстрации первого случая рассмотрим одномерную динамическую систему
xў = -x2+e (3)
При e < 0 эта система очевидно не имеет стационарных точек. При e = 0 происходит рождение полуустойчивой стационарной точки, которая при e > 0 превращается в две ѕ устойчивую и неустойчивую. Эта бифуркация в некотором смысле типична. В многомерном случае соответствующая типичная бифуркация, отвечающая наличию у матрицы A(0) нулевого собственного значения, получается как результат приписывания к уравнению (3) гиперболической системы (рис. 3).
Литература:
Систематическое описание бифуркаций двумерных динамических систем Современное изложение результатов и методов можно найти в [Арнольд, Итоги науки и техники..., Марсден ѕ Мак-Кракен].
Применение теории индекса к исследованию бифуркаций описано в [ Красносельский, Красносельский ѕ Забрейко].
И еще про тренды от него же:
Есть (как реальность) тренды. НО невозможно рассчитать, какая именно точка - есть начало/конец тренда.
Но из того, что это нельзя рассчитать НЕ следует, что трендов нет.
Из этого следует только то, что этого НЕВОЗМОЖНО рассчитать, то бишь нельзя заработать денег на таких расчетах. При бэк-тестинге, используя оптимизацию (читай: подгон результатов), можно, но с реальной правой стенкой — нет.
ПОЭТОМУ, когда ваша «система» будет делать поправку на тренд — тренд, может быть, уже поменялся...
НЕВОЗМОЖНО рассчитать точку разворота тренда. Это — математически неразрешимая задача.
Прочитал. Где то подобное уже видел, не помню. Пять характеризующих равновесное состояние точек… Тут не хватает деталей, чтобы иметь возможность дать конкретное мнение. Вообще, в подобных работах вся суть подхода кроется в деталях. Про которые никто толком не пишет.
У меня немного схожий подход. Но я не заморачиваюсь на пять фаз состояния, не заморачиваюсь с нормализацией (это отдельный геморрой со своими нюансами динамического характера). У меня на выходе всегда +1 или -1, т.е. качественная оценка. Вероятность движения оцениваю совсем по другому. Интерес и объемы не участвуют в расчетах. Количественная оценка — импульс.
И еще — мне не нравится, что в таких работах конкретизируется период времени (здесь — 10 дней). Это, на мой непросвещенный взгляд, сразу частный случай и в принципе не верно. У меня нет привязки к фрейму или периоду, полное масштабирование.