Блог им. uralpro
Импульсная стратегия на традиционных и криптовалютах. Часть 1
- 09 мая 2017, 13:18
- |
Перевод основных моментов статьи «Momentum in traditional and cryptocurrencies made simple» Janick Rohrbach, Silvan Suremann, Joerg Osterrieder. Статья интересна последовательным подходом к разработке алгоритма, обходясь при этом очень простой математикой.
Введение
Импульс это традиционная стратегия для торговли валютами. Растущие ранее активы с большей вероятностью продолжат свой рост, ранее падающие продолжат падение. Для исполнения такой стратегии нужно покупать дорожающие валюты и продавать дешевеющие. Мы используем алгоритм, представленный в Baz, J., Granger, N., Harvey, C.R., Le Roux, N., Rattray, S., 2015. Dissecting investment strategies in the cross section and time series., для генерации импульсных сигналов, основанных на пересечениях трех экспоненциальных скользящих средних с различными временными горизонтами. Эти три скользящие средние определяют короткий, средний и долгосрочный тренд. В упомянутой статье было показано, что этот подход работает хорошо для различных классов активов. Мы возьмем только валютный рынок и детально покажем, как алгоритм работает применительно к нормально распределенным приращениям. Затем мы используем алгоритм для бэктеста на реальных данных и продемонстрируем, на каких периодах стратегия работает, а на каких — нет.
Алгоритм
В этом разделе разберем, как алгоритм работает в в случае нормально распределенных приращений.
Нормально распределенные приращения цены
Для симуляции цен с нормально распределенными приращениями используем геометрическое броуновское движение (ГБД). Оно описывается следующим стохастическим диффренциальным уравнением:
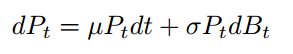
где B_t - стандартное броуновское движение. Используя лемму Ито, запишем решение этого уравнения:
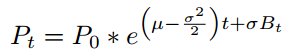
ГБД предполагает постоянную волатильность, что упрощает модель по сравнению с реальными валютными ставками, где волатильность меняется со временем.
Установим цену валютной пары в момент времени t=0 как S_0=1. Ожидаемый годовой доход определим как μ=0, предположив, что тренда нет. Таким образом, наш сконструированный временной ряд представляет собой ряд Мартингейла.
Просвоим значению годовой волатильности величину σ=0.05, что примерно соответствует годовой волатильности пары EUR/USD.
Сгенерируем временной ряд за 100 лет (t=1,2,...,100) с размером шага Δt=1/365.24. Отметим, что у нас нет различия между рабочими и выходными днями. Таким образом, наш временной ряд имеет 365.24 точек в год вместо 252. Случайная выборка показана на рисунке:
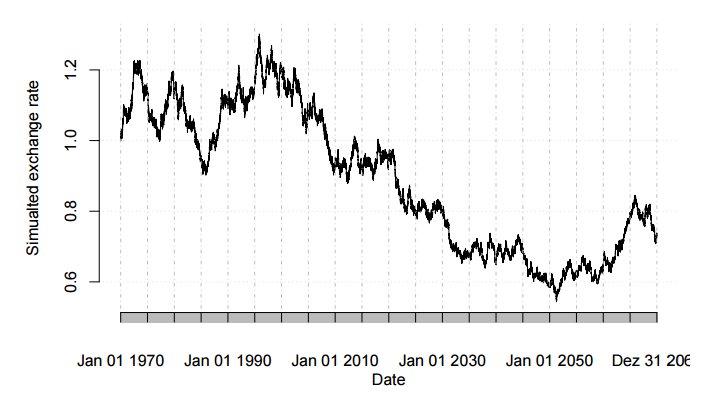
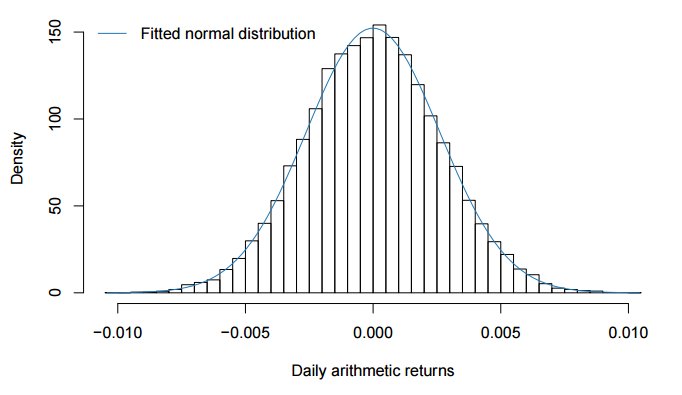
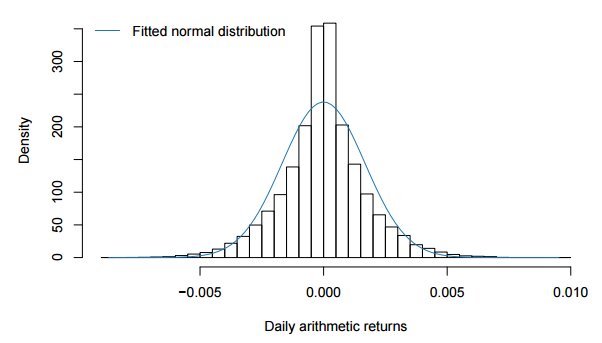
На следующем рисунке показаны дневные приращения цены, вычисленные как
![]()
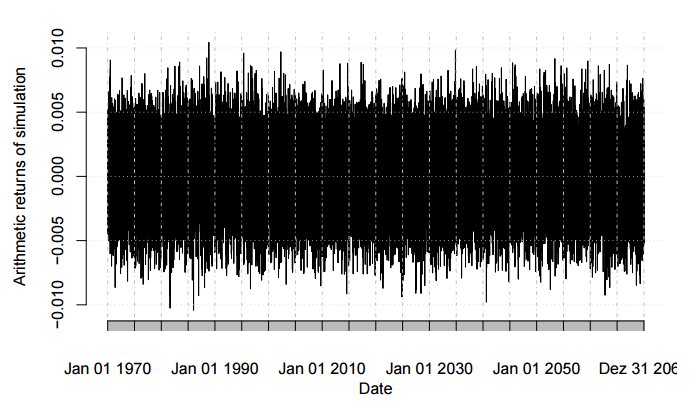
Дневные арифметические приращения распределены нормально, как показано на рисунке в заглавии.
Экспоненциальная скользящая средняя
Экспоненциальная скользящая средняя (ЕМА) это фильтр с экспоненциально снижающимися весами. Следующая формула показывает рекурсивное вычисление EMA:
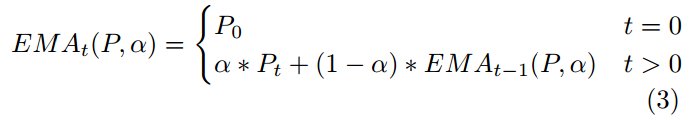
где α=1/n - экспоненциальный сглаживающий коэффициент.
Пересекающиеся ЕМА с различными временными периодами
Выберем три различных временных периода, каждый со своим значением n_k для краткосрочных и длинносрочных ЕМА. Определим n_k,s=(8,16,32) для краткосрочных ЕМА и n_k,l=(24,48,96) для долгосрочных ЕМА.
Отметим, что n_k не является ни длительностью, ни временем «полураспада». Длительность ЕМА в точке t всегда равна [0,t] и следующее уравнение вычисляет время «полураспада»:
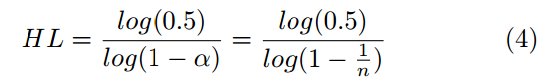
Таблица 1 показывает время полураспада для каждого n_k. Увеличение n_k в два раза влечет увеличение времени «полураспада» примерно вдвое.

Чтобы рассмотреть пересечения ЕМА мы расширим имитацию нашей серии для 2050 года. Рисунок ниже демонстрирует ЕМА для k=1. Это означает n_k,s=8 и n_k,l=24.Там, где короткая ЕМА проходит выше длинной мы имеем положительный тренд, а там, где короткая ЕМА проходит ниже длинной, тренд отрицательный. Рисунки ниже показывают ЕМА для k=2 и k=3 соответственно.
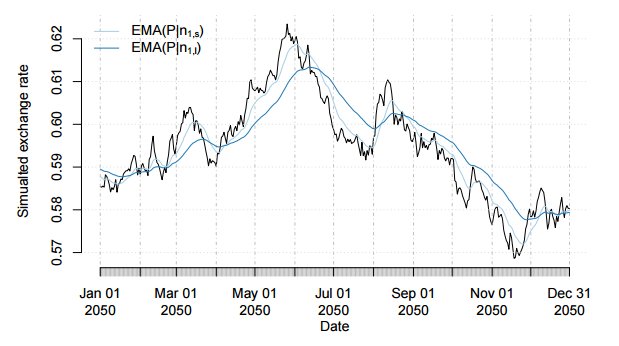
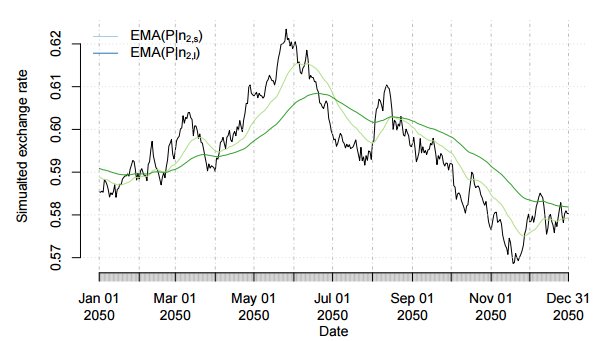
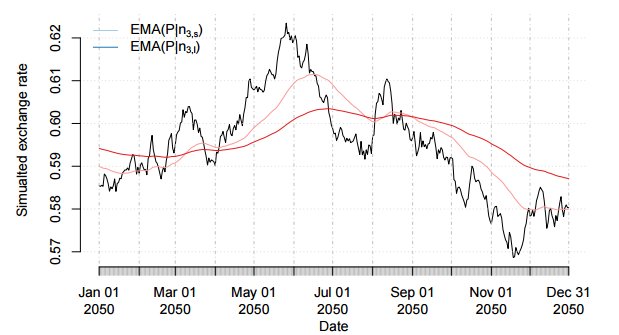
Можно отметить, что ЕМА фильтры в основном работают правильно. Тем не менее, есть задержка при смене тренда от положительного к отрицательному и наоборот. Посмотрим на окончание позитивного тренда в мае 2050 года. Желательно, чтобы короткая ЕМА пересекала бы длинную ЕМА вверху той же даты. Но занимает несколько недель, чтобы эти ЕМА пересеклись. Чем больше n_k, тем больше времени пройдет до точки пересечения, которая сигнализирует смену тренда. С другой стороны, больший n_k менее подвержен флюктуациям на длительном тренде. Используя уравнение для ЕМА, вычислим:
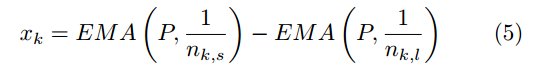
где k=1,2,3.
Рисунок ниже показывает результаты вычислений для k=1,2,3. Положительное значение x_k означает положительный тренд, в то время, как отрицательное значение означает тренд понижающийся. x_k=0 когда короткая ЕМА пересекает длинную, таким образом обозначая смену направления тренда. x_k наш первый сигнал. Он определяет когда мы должны быть в длинной или короткой позиции по данной валюте.
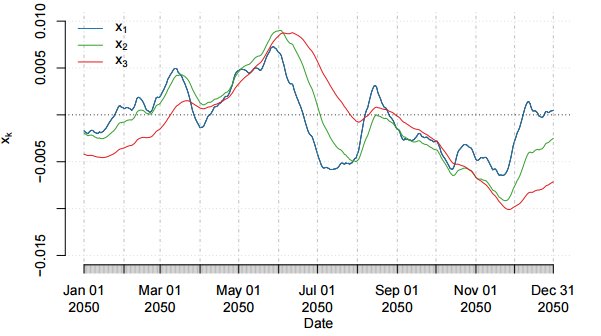
Нормализация
Далее мы проведем нормализацию с помощью трехмесячного скользящего стандартного отклонения цены валютной пары. Это преобразование приводит сигнал каждой валюты к одинаковой амплитуде. Рисунок демонстрирует результат.
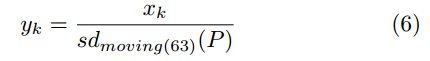
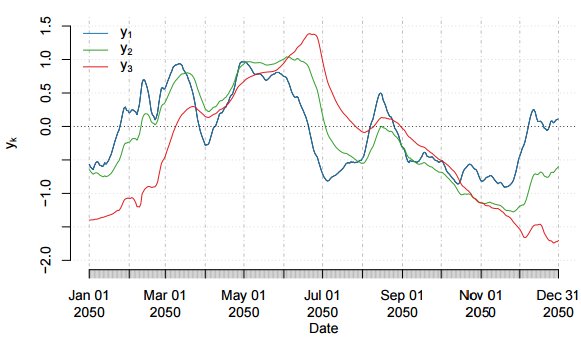
Полученный временной ряд нормализуется снова с помощью скользящего стандартного отклонения за 1 год. Это преобразование позволяет сделать волатильность более приближенной к постоянному значению. Рисунок демонстрирует результат.
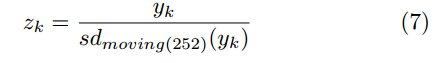
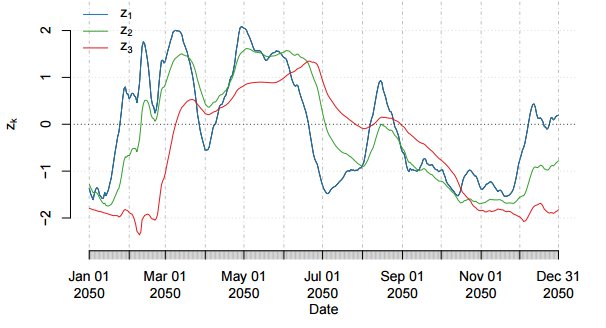
Генерация сигнала
Применим нижеследующую функцию реакции для вычисления u_k:
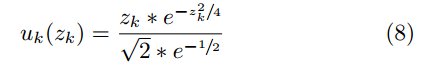
В знаменателе значение выражения равно 0.858. Как выводилось выражение для u_k можете посмотреть в оригинале статьи.
Как показано на рисунке ниже, функция реакции отражает каждое значение z_k на u_k внутрь диапазона [-1,1]. Функция имеет глобальный минимум в точке z_k=−(√2) при u_k(−(√2))=−1 и глобальный максимум в z_k=(√2) при u_k(√2)=1. Таким образом, значение сигнала всегда лежит между -1 и 1.
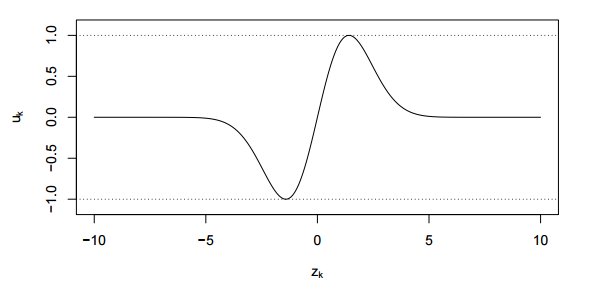
Взяв взвешенную сумму всех u_k мы вычислим итоговый сигнал:
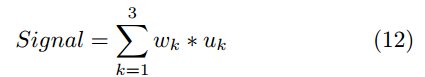
где w_k=1/3. Вы можете использовать другие веса, общая сумма которых будет равна 1, но мы решили взять равные веса для простоты. Сигнал выглядит так:
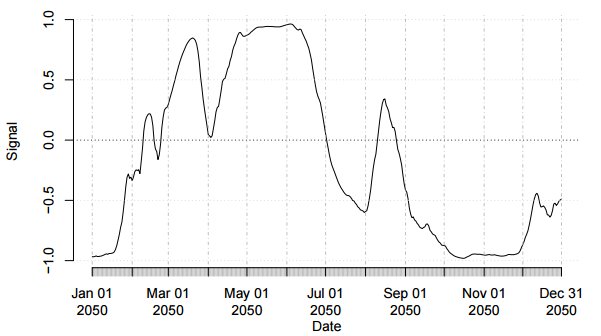
По этому сигналу мы сделали бэктест по сгенерированным данным путем перемножения дневных арифметических приращений временной серии на сигнал прошедшего дня. Рисунок показывает кумулятивный профит за 100 лет:
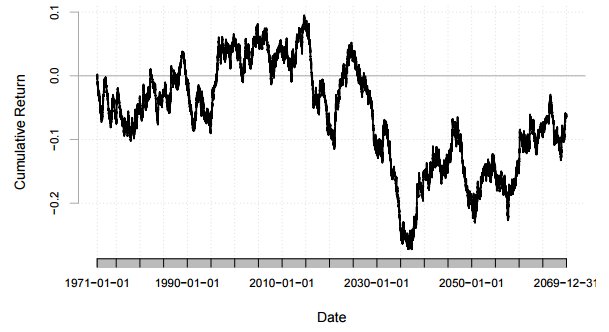
Далее посмотрим на гистограмму дневных приращений нашей стратегии на рисунке ниже. Можно увидеть, что приращения симметрично распределены со средним, равным 0. Это именно то, что мы ожидали, то есть импульсы цены в сгенерированных данных отсутствуют. Ожидаемая кумулятивная прибыль также равна 0. Результат говорит о том, что наши вычисления верны и мы можем сейчас применить такой же алгоритм на реальных рыночных данных.
В следующей части мы продемонстрируем работу алго на реальных данных с рынков традиционных и криптовалют.
Продолжение и другие стратегии и алгоритмы автоматической торговли смотрите на моем сайте www.quantalgos.ru


теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R




















x = — 1/l * lnа :) в формуле скользящей средней я это не видел даже близко.
П.С. Классически средних — арифметическая, геометрическая и гармоническая. Все остальные от лукавого. :)
cs229.stanford.edu/proj2013/TakeuchiLee-ApplyingDeepLearningToEnhanceMomentumTradingStrategiesInStocks.pdf
про листовая бегло пост, не смотря кто автор, понял что автором может быть только uralpro , и какое же было удивление что так и оказалось :)
++++