SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. egenui
Quantitative trading for dummies. Part 1 (Линейная регрессия)
- 27 июня 2015, 23:39
- |
Добрый день. Решил начать цикл статей на модную нынче тему Quantitative trading / data minig / machine learning. Сегодняшняя тема будет посвящена построении модели линейной регрессии цен закрытия акций GAZP и LKOH.
Линейная регрессия представляет из себя метод регрессионного анализа, если обратиться к статье на вики, то определение регрессионного анализа звучит таким образом:
Регрессио́нный анализ — статистический метод исследования влияния одной или нескольких независимых переменных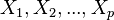 на зависимую переменную
на зависимую переменную  . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
Чем это может дать нам, как трейдерам. Представьте что независимые переменные X1,X2,....Xp (предикты) есть не что иное как стоимость акций компаний X1,X2,....Xp а Y есть стоимость акий компании Y. И существует функция которая описывает стоимость актива Y. F(X1,X2,..Xp)=Y, соответственно мы можем предсказать по предиктам X значение Y.
Существует множество типов регрессий, но в основе из них лежит одна и та же идея: построить модель, связывающую предсказываемое значение с исходными данными (предиктами). Простейший вариант из регрессий которых мы рассмотрим в статье — Линейная регрессия. Линейная она от того что представляет из себя линейное уравнение y=a+b*x В данной статье рассмотрим пример линейной регрессии с одним предиктом, и одной предсказываемой величиной. Такую регрессию можно нарисовать на графике X,Y. Для этого по оси абсцисс X мы отмечаем значения предиктора, а по оси ординат Y значения предсказываемой величины. В качестве предикта я буду использовать цену закрытия GAZP а в качестве предсказываемой величины цену закрытия LKOH. Таким образом наше уравнение сводится к виду LKOH.Close = GAZP.Close*b+ КОНСТАНТА, а сама задача примет вид: найти коэффициенты a и b минимизирующие величину ошибки. Если мы можем определить константу и коэффициент, то мы можем по цене GAZP предсказывать цену акции LKOH, исли возникает отклонение, то можно купить спред и на этом заработать, в теории. И так, что же такое линейная регрессия. Для начала чуть чуть теории, без нее будет сложновато, формул не будет(ну практически)!
Линия регрессии
Построим модель
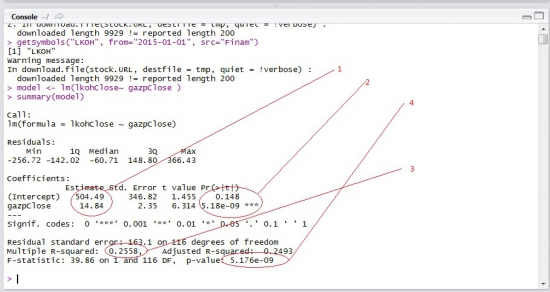
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков (Residuals): минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, это очень важно! Это мы сделаем ниже.
Гипотеза линейной регрессии
Коэффициенты (1) это значения которые мы подставляем в линейное уравнение. LKOH.Close = GAZP.Close*14.84+504.49. Помимо этого R нам показывает величину ошибок или стандартное отклонение для каждого коэффициента. Нам так же интересно, объясняют ли вообще хоть что-нибудь наши коэффициенты. Чтобы проверить это, мы, выдвигаем нулевую гипотезу, что, к примеру коэффициент 504.49 является лишь результатом погрешности и его значением можно пренебречь. Для проверки такой гипотезы, используется t-критерий Стьюдента. Здесь R вычисляет как саму величину t так и степень значимости нашей гипотезы Pr(>|t|). Так, в нашем случае величина (2) 0.148 означает что мы на 100*(1-0.148) = 85.2% уверены в том, что свободный член в нашем выражении отличен от нуля.
Оценка качества линейной регрессии: коэффициент детерминации R2
Коэфицент R2 (Multiple R-squared)(3), так же его называют коэффициентом детерминации, описывает насколько точно наша модель описывает данные, он показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Чем ближе величина этих значений к 1, тем лучше. 1 это идеальный результат, означающий, что модель на 100% описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей. Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат (Adjusted R-squared). Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
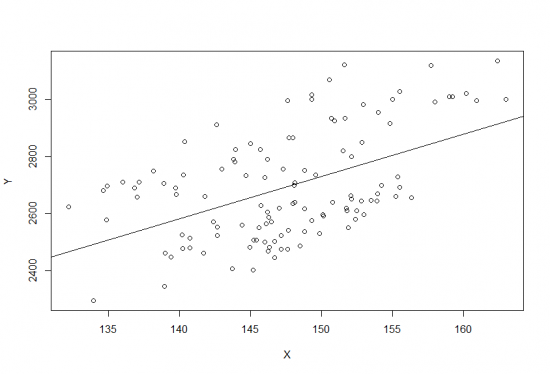
И, наконец, мы можем проверить, насколько предсказываемая величина зависит от предикторов(F-statistic). Для этого выдвигается нулевая гипотеза, что предсказываемая величина вообще не зависит от предикторов. для этой гипотезы определяется p-значение (4). В нашем случае, оно получилось равным 5.176e^-09. т.е. 99.99948%, что предсказываемая величина действительно зависит от предикторов. Обычно, имеет смысл смотреть на этот параметр в первую очередь. График чуть выше, как раз показывает наши данные и результат линейной регрессии.
Диагностика, и ошибки модели.
Чтобы модель была корректной, необходимо выполнение условий Гаусса-Маркова, т.е. ошибки должны быть гомоскедастичны с нулевым математическим ожиданием. Построим графики нашей модели, по сути все они из себя представляют модель линейной регрессии, однако в качестве данных для модели, они используют данные полученные из линейной модели ваших данных, и рассмотрим некоторые из них.
Fitted values — значения y, которые были получены (не путайте с Y - это значения которые были данны. см выше).
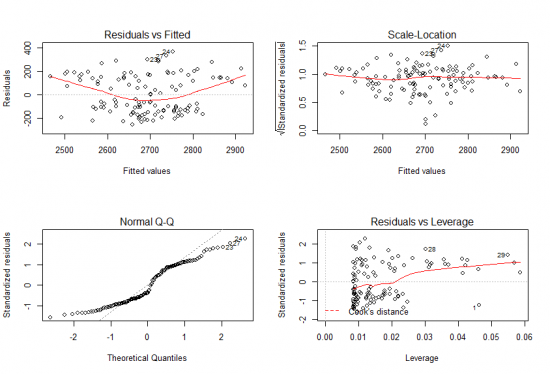
График (Residuals vs Fitted) График распределения остатков, могут быть как положительны так и отрицательны. На нем мы должны наблюдать случайно распределение остатков с нулевым средним значением. На первый взгляд остатки более-менее равномерно распределены относительно горизонтальной оси, что говорит об «отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях». Однако, как мы увидим ниже, это не так! Обратите внимание, некоторые точки пронумерованы, это точки которые требуют особого внимания.
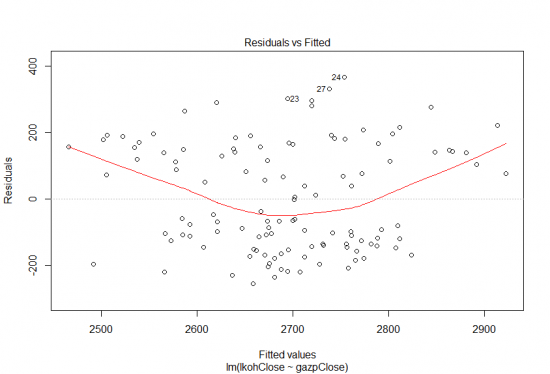
А теперь исследуем такой же график, но построенный для линейной модели, которая на самом деле не линейна:
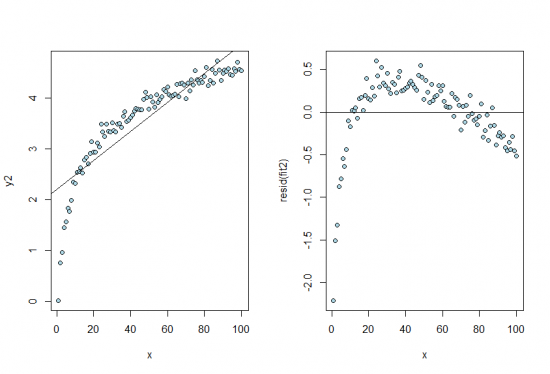
По левому графику можем заметить что вроде бы существует линейная зависимость, но у остатков есть паттерн (оно точно не нормально распределено) так что линейная модель тут не подходит.
График (Normal Q-Q) График зависимости квантилей остатков против квантилей, которые можно было бы ожидать при условии, что остатки нормально распределены. Напомню, что одно из предположений регрессии наименьших квадратов является то, что ошибки распределены нормально. Точки на графике должны лежит максимально близко линии регрессии, некоторые отклонения можно ожидать на концах, но они должны быть небольшие, в нашем случае отклонения достаточно велики. Можем наблюдать что предложение о нормальности остатков можно опровергнуть, что говорит о некорректности модели.
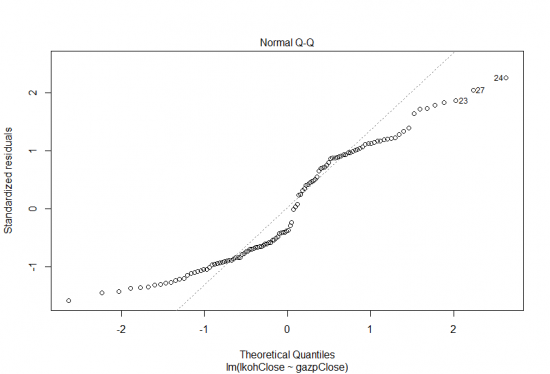
Заключение. Статья получилась гораздо больше чем ожидал в начале. Данный материал может существенно помочь вам в парном трейдинге. Надеюсь статья была вам полезна. Что же дальше? Думаю продолжить с темами корреляции и коинтеграции, если же конечно данная статья вызовет хоть какой-нибудь интерес.
Линейная регрессия представляет из себя метод регрессионного анализа, если обратиться к статье на вики, то определение регрессионного анализа звучит таким образом:
Регрессио́нный анализ — статистический метод исследования влияния одной или нескольких независимых переменных
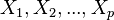 на зависимую переменную
на зависимую переменную  . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.Чем это может дать нам, как трейдерам. Представьте что независимые переменные X1,X2,....Xp (предикты) есть не что иное как стоимость акций компаний X1,X2,....Xp а Y есть стоимость акий компании Y. И существует функция которая описывает стоимость актива Y. F(X1,X2,..Xp)=Y, соответственно мы можем предсказать по предиктам X значение Y.
Существует множество типов регрессий, но в основе из них лежит одна и та же идея: построить модель, связывающую предсказываемое значение с исходными данными (предиктами). Простейший вариант из регрессий которых мы рассмотрим в статье — Линейная регрессия. Линейная она от того что представляет из себя линейное уравнение y=a+b*x В данной статье рассмотрим пример линейной регрессии с одним предиктом, и одной предсказываемой величиной. Такую регрессию можно нарисовать на графике X,Y. Для этого по оси абсцисс X мы отмечаем значения предиктора, а по оси ординат Y значения предсказываемой величины. В качестве предикта я буду использовать цену закрытия GAZP а в качестве предсказываемой величины цену закрытия LKOH. Таким образом наше уравнение сводится к виду LKOH.Close = GAZP.Close*b+ КОНСТАНТА, а сама задача примет вид: найти коэффициенты a и b минимизирующие величину ошибки. Если мы можем определить константу и коэффициент, то мы можем по цене GAZP предсказывать цену акции LKOH, исли возникает отклонение, то можно купить спред и на этом заработать, в теории. И так, что же такое линейная регрессия. Для начала чуть чуть теории, без нее будет сложновато, формул не будет(ну практически)!
Линия регрессии
Разместим точки на двумерном графике и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией. Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bx.
- x называется независимой переменной или предиктором.
- Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0. ( так же его называют константой)
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b
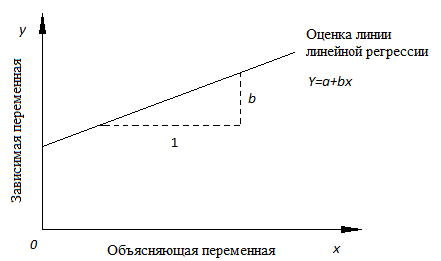
Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Мметод наименьших квадратов
- Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β, которые определяют линию линейной регрессии в популяции (генеральной совокупности).
- Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
- Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y).
- Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
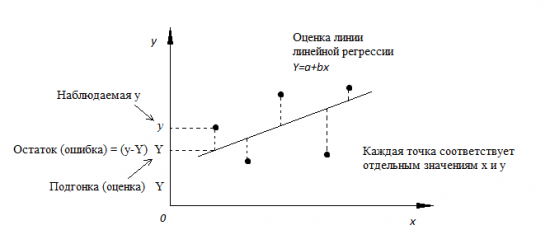
Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки..
Практика
Для начала нам понадобятся данные
getSymbols("GAZP", from="2015-01-01", src="Finam")
getSymbols("LKOH", from="2015-01-01", src="Finam")
Далее создадим вектора из цен закрытия gazpClose <- as.vector(GAZP$GAZP.Close) lkohClose <- as.vector(LKOH$LKOH.Close)Построим линию регрессии
plot(lkohClose~ gazpClose, ylab = 'Y', xlab='X' ) abline(model)

Построим модель
model <- lm(lkohClose~ gazpClose )<br />summary(model)

Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков (Residuals): минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, это очень важно! Это мы сделаем ниже.
Гипотеза линейной регрессии
Коэффициенты (1) это значения которые мы подставляем в линейное уравнение. LKOH.Close = GAZP.Close*14.84+504.49. Помимо этого R нам показывает величину ошибок или стандартное отклонение для каждого коэффициента. Нам так же интересно, объясняют ли вообще хоть что-нибудь наши коэффициенты. Чтобы проверить это, мы, выдвигаем нулевую гипотезу, что, к примеру коэффициент 504.49 является лишь результатом погрешности и его значением можно пренебречь. Для проверки такой гипотезы, используется t-критерий Стьюдента. Здесь R вычисляет как саму величину t так и степень значимости нашей гипотезы Pr(>|t|). Так, в нашем случае величина (2) 0.148 означает что мы на 100*(1-0.148) = 85.2% уверены в том, что свободный член в нашем выражении отличен от нуля.
Оценка качества линейной регрессии: коэффициент детерминации R2
Коэфицент R2 (Multiple R-squared)(3), так же его называют коэффициентом детерминации, описывает насколько точно наша модель описывает данные, он показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Чем ближе величина этих значений к 1, тем лучше. 1 это идеальный результат, означающий, что модель на 100% описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей. Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат (Adjusted R-squared). Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
И, наконец, мы можем проверить, насколько предсказываемая величина зависит от предикторов(F-statistic). Для этого выдвигается нулевая гипотеза, что предсказываемая величина вообще не зависит от предикторов. для этой гипотезы определяется p-значение (4). В нашем случае, оно получилось равным 5.176e^-09. т.е. 99.99948%, что предсказываемая величина действительно зависит от предикторов. Обычно, имеет смысл смотреть на этот параметр в первую очередь. График чуть выше, как раз показывает наши данные и результат линейной регрессии.
Диагностика, и ошибки модели.
Чтобы модель была корректной, необходимо выполнение условий Гаусса-Маркова, т.е. ошибки должны быть гомоскедастичны с нулевым математическим ожиданием. Построим графики нашей модели, по сути все они из себя представляют модель линейной регрессии, однако в качестве данных для модели, они используют данные полученные из линейной модели ваших данных, и рассмотрим некоторые из них.
Fitted values — значения y, которые были получены (не путайте с Y - это значения которые были данны. см выше).
layout(matrix(1:4,2,2)) plot(model)

График (Residuals vs Fitted) График распределения остатков, могут быть как положительны так и отрицательны. На нем мы должны наблюдать случайно распределение остатков с нулевым средним значением. На первый взгляд остатки более-менее равномерно распределены относительно горизонтальной оси, что говорит об «отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях». Однако, как мы увидим ниже, это не так! Обратите внимание, некоторые точки пронумерованы, это точки которые требуют особого внимания.

А теперь исследуем такой же график, но построенный для линейной модели, которая на самом деле не линейна:
x <- c(1:100) n <- 100 y2 <- log(x) + rnorm(n, sd=.1) fit2 <- lm(y2 ~ x) layout(matrix(1:2,1,2)) plot(x, y2, pch=21, col="black", bg="lightblue") abline(fit2) plot(x, resid(fit2), pch=21, col="black", bg="lightblue") abline(h=0)

По левому графику можем заметить что вроде бы существует линейная зависимость, но у остатков есть паттерн (оно точно не нормально распределено) так что линейная модель тут не подходит.
График (Normal Q-Q) График зависимости квантилей остатков против квантилей, которые можно было бы ожидать при условии, что остатки нормально распределены. Напомню, что одно из предположений регрессии наименьших квадратов является то, что ошибки распределены нормально. Точки на графике должны лежит максимально близко линии регрессии, некоторые отклонения можно ожидать на концах, но они должны быть небольшие, в нашем случае отклонения достаточно велики. Можем наблюдать что предложение о нормальности остатков можно опровергнуть, что говорит о некорректности модели.

Заключение. Статья получилась гораздо больше чем ожидал в начале. Данный материал может существенно помочь вам в парном трейдинге. Надеюсь статья была вам полезна. Что же дальше? Думаю продолжить с темами корреляции и коинтеграции, если же конечно данная статья вызовет хоть какой-нибудь интерес.
3.6К |
Читайте на SMART-LAB:

📈 Потенциал роста акций МГКЛ составляет 89% — ИБ Синара
Аналитики Банка Синара обновили оценку по ПАО «МГКЛ» с учётом сильных операционных результатов компании. Новая целевая цена установлена на...
11:44
Флоатеры 2026: что это и как заработать до 15,7%
Как устроены и насколько актуальны в 2026 г. флоатеры, или облигации с плавающим купоном? Как инвестировать во них легко? Подробно на все вопросы...
11:19
теги блога evgen000
- AlfaDirect
- Asset Allocation
- DrVaska
- Excel
- goldman sachs
- HFT
- machine learning
- OTC
- portfolio managment
- quantitative research
- Quantitative trading
- RTS
- Soros
- SPY
- United Traders
- WealthLab
- Yahoo
- акции
- алготрейдинг
- альфа директ
- биржа
- василий олейник
- Газпром
- ГК ПИК
- дизайн
- жизнь
- инвест идея
- Индекс оптимизма смарт-лаб
- интервью
- Ипотечные ценные бумаги
- кванты
- Керимов
- книга
- конференция
- корреляции
- Лукойл
- Мамут
- машинное обучение
- ммвб
- навыки трейдера
- ОФЗ
- оффтоп
- парная торговля
- Паха
- ПИК
- прогнозы
- Путен
- Ральф Винс
- РЕПО
- рынок
- система торговли
- смартлаб
- смартлаб конкурс
- Спред
- ставки
- Статьи
- стратеги
- терминал
- технический анализ
- Уралкаий
- Финам
- фьючерс РТС волатильность
- хедж-фонд





















en.wikipedia.org/wiki/Renaissance_Technologies
в чём отличие от мувинг-авередж в двух словах?
Алгоритмы регрессии же позволяет оценивать зависимость чего-то от чего-то другого.
Респект.
вызовет. нужное дело делаете, обязательно пишите еще.