мне как-то амеровский кванты втирали на сикингэлфе про граали на плеыевых итиэфах… ну я им показал что они не правы…
ПГУ мехмат, дык сказать)))
я бы меньше ссылался на seekin'alpha… там публика сомнительная какаято)
плотность распределения
Плотность распределения (frequency distribution) — отражение данных, распределенное по небольшим интервалам. Помогает в анализе больших объемов данных и работает со всеми шкалами измерений. Важно понимать, что основная задача плотноси распределения — это суммировать большой объем данных и упростить работу с ними.
Как построить плотность распределения?
Например у нас есть данные по месячной доходности индекса S&P500 за последние 100 лет.
количество измерений в 1 интервале — абсолютная частота (absolute frequency)
Относительная частота (relative frequency) — абс. частота поделенная на общее количество измерений.
если у нас есть большое количество пустых интервалов, то можно уменьшить k.
Пример плотности распределения ежемесячной доходности индекса S&P500 с января 1950 по сентябрь 2009, представленный в виде гистограммы распределения[1]:
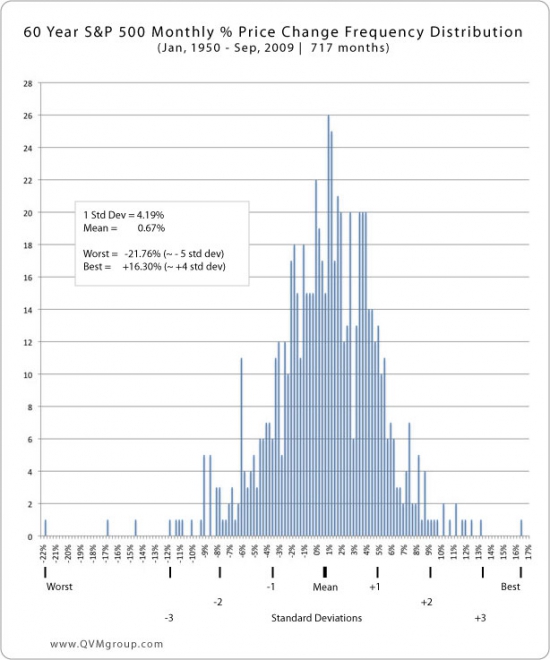
еще 1 способ отражения данных:
frequency polygon (многоугольник частот) — тоже самое, но построенное не в виде линее, а по средним точкам диапазонов в виде многоугольника.
Выглядит он примерно вот так:
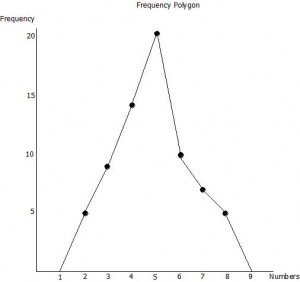
еще 1 способ отражения — кумулятивная кривая распределения (cumulative frequency distribution):
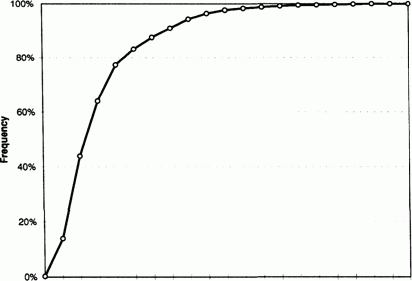
Источники:
1. http://seekingalpha.com/article/168445-s-p-500-price-change-frequency-distributions
Интересные ссылки по теме:
статистические модели трендов. Смещение среднего. (02.2012)
Как построить плотность распределения?
Например у нас есть данные по месячной доходности индекса S&P500 за последние 100 лет.
- Отсортировать данные по возрастанию.
- вычислить диапазон (макс значение — мин значение)
- Определить кол-во интервалов, k
- определить ширину интервала, = диапазон/k
- поделить шкалу от минимального значения к максимальному на равномерные интервалы
- определить количество данных, которые попали в каждый из интервалов
- составить таблицу интервалов с количеством попаданий значений в каждый из них.
количество измерений в 1 интервале — абсолютная частота (absolute frequency)
Относительная частота (relative frequency) — абс. частота поделенная на общее количество измерений.
если у нас есть большое количество пустых интервалов, то можно уменьшить k.
Пример плотности распределения ежемесячной доходности индекса S&P500 с января 1950 по сентябрь 2009, представленный в виде гистограммы распределения[1]:

еще 1 способ отражения данных:
frequency polygon (многоугольник частот) — тоже самое, но построенное не в виде линее, а по средним точкам диапазонов в виде многоугольника.
Выглядит он примерно вот так:

еще 1 способ отражения — кумулятивная кривая распределения (cumulative frequency distribution):

Источники:
1. http://seekingalpha.com/article/168445-s-p-500-price-change-frequency-distributions
Интересные ссылки по теме:
статистические модели трендов. Смещение среднего. (02.2012)

















