Ухмылка неопределенности для трендовых стратегий

Сегодня все будет просто — мы будем строить идеальную торговую систему. При этом наша система будет трендовой, с характерным временем удержания позиции или, иначе говоря, горизонтом прогноза.

Сейчас мы ещё не научились ничего предсказывать, и не знаем ничего о том что там происходит на рынках — работают там тренды, контр.тренды, или фундаментальный анализ. Поэтому заменим наше настоящее незнание идеальной моделью, заглядывающей в будущее на определенный горизонт и, соответственно, обладающей идеальной предсказательной силой.

Дадим нашей модели 5 лет истории золота, таймфрейма м15 и попросим ее показать нам мастер класс:


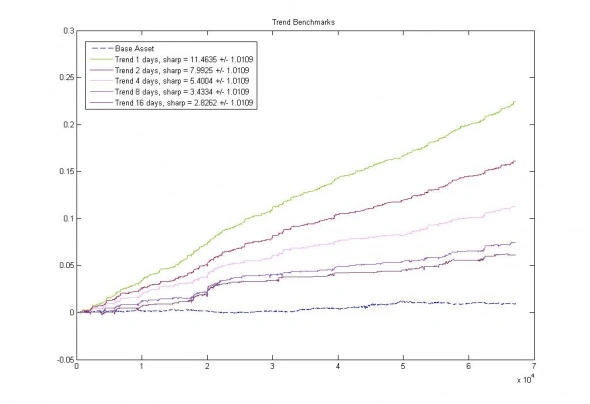
Рис 1. Базовый актив (Золото) и результаты сверх идеальных ценовых торговых систем в зависимости от времени удержания позиции, учитывая издержки


Видно, что даже сверх идеальная модель теряет предсказательную силу с ростом горизонта прогноза приблизительно пропорционально корню из времени. К тому же, в этом модельном эксперименте мы все таки немного смухлевали, предположив, что наша идеальная модель видит априорно неточное будущее идеально точно. На самом деле, если будущее  туманно, то и его ясновидение может быть исключительно туманным. А когда одна неопределенность (видение) описывает другую неопределенность (будущее), как известно, возникает улыбка неопределенности)))

Теперь проведем эксперимент честно — покажем нашей модели будущее столь же туманным, каким оно является в действительности, и посмотрим, какой результат ей удастся показать при помощи подглядывания через туман:


Рис. 2.  Базовый актив (Золото) и результаты идеальных ценовых торговых систем в зависимости от времени удержания позиции, учитывая издержки, с учетом шумовой неопределенности прогнозов
 

Удивительно, но три раза из пяти проиграть B&H умудрилась даже ясновидящая модель, в условиях когда будущее оказалось спрятанным за шумом! При этом даже для подглядывающей в будущее модели на горизонтах прогноза выше 1 дня, глубина выборки в 5 лет оказалась ничтожна, для того, чтобы можно было статистически достоверно судить о способностях этой идеальной модели. 


С точки зрения математики оказалось достаточным лишь вести в точное значение будущего Y гетероскедастичный остаток, заданный уравнением :

Y* = Y + ( 1 — | Y | )*epsilon, epsilon ~N(0,1)