29 мая 2021, 11:15
Критическая масса и критическое значение - большой эмпирический тест
Ранее, и в ходе дискуссий, мы получили три статистических оценки для качества аппроксимации данных длинной L (коэффициент Шарпа) со стороны случайных наборов коррелированных признаков (Features) размерностью N и корреляционной матрицей C.
Для случайного признака :
Для лучшего признака из набора :
Для портфеля признаков (композитное решение) :
Где D — дисперсия прямой суммы нормированных признаков :
Ne — эффективная размерность признакового пространства, обладающая аналогичной суммарной дисперсией с учетом повторений признаков:
Проведем серию испытаний для 10 000 случайно сгенерированных случайно коррелированных наборов признаков, обладающих случайной задающей пространство размерностью и построим распределение отношения статистики критерия (sharp) к критическому уровню (Z), для доверительной вероятности 50% (медиана).
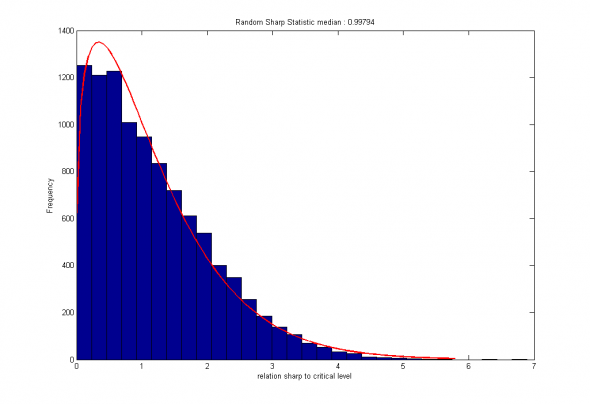
Рис 1. Распределение относительной величины статистического критерия для случайно выбранного признака. Медиана = 0.998
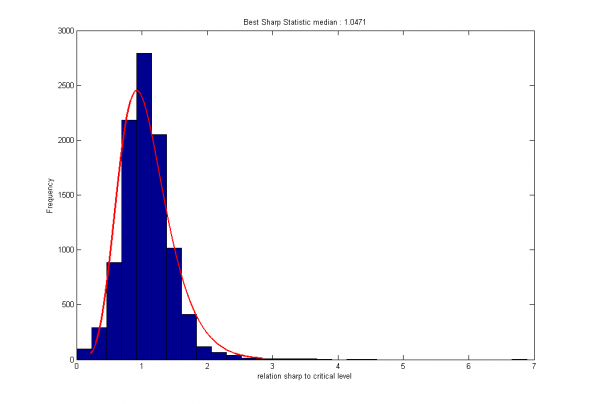
Рис 2. Распределение относительной величины статистического критерия для лучшего выбранного признака. Медиана = 1.047
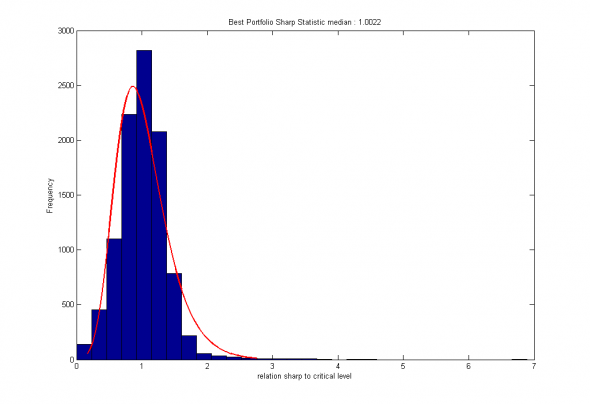
Рис 3. Распределение относительной величины статистического критерия для портфеля признаков (Boosting). Медиана = 1.002
Видно, что выборочная оценка медианного значения относительной статистики не отклоняется от 1 сильнее, чем на 0.047, при асимптотическом СКО порядка 0.04.
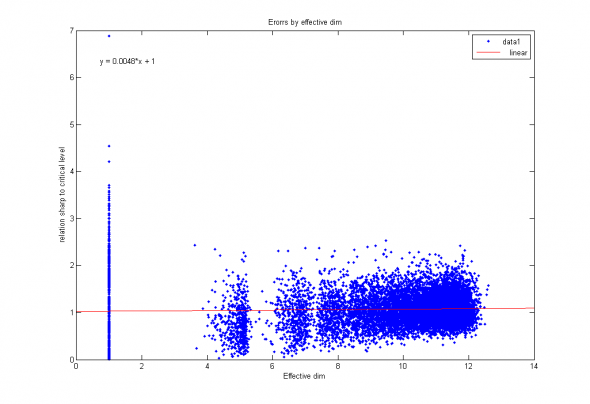
Рис. 4. Слабая зависимость среднего относительных статистик в зависимости от расчетной размерности признакового пространства.
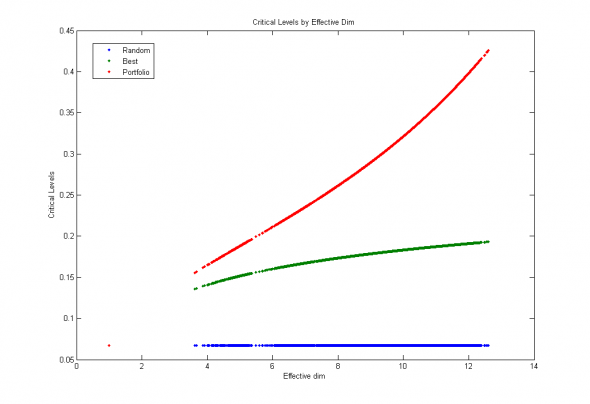
Рис 5. Оценка медианы качества аппроксимации данных различными алгоритмами в зависимости от эффективной размерности признакового пространства.
Прил. Код Матлаб:
function BigRandomTest(N,K,L)
%BIGRANDOMTEST производит генерацию N выборок длинной L
% и размерностью K коррелированных случайных стратегий и расчитывает их
% статистические характеристики
X=zeros(L,K); % случайная матрица признаков
z=zeros(N,3); % результаты эмпирические
lim=zeros(N,3); % результаты теоретические
Narr=zeros(N,1); % результаты рассчета эффективной размерности
l=ones(1,K); y=ones(L,1);
warning('off','all');
for i=1:N
X=genRS(K,L); % случайная смешанная матрица
C=corr(X); % корреляционная матрица
C=abs©;
% Рассчитываем пределы
lim(i,1)=(2/L)^0.5*erfinv(0.5); % шарп случайной стратегии
Ne=1+0.5*(2*K-1-(4*l*C*l'-4*K+1)^0.5); Narr(i)=Ne;
lim(i,2)=(2/L)^0.5*erfinv(0.5^(1/Ne)); % шарп лучшей стратегии из множества
lim(i,3)=lim(i,2)*(K.^2/(l*C*l'))^0.5;
% Рассчитываем статистики
sharp=abs(mean(X)./std(X));
z(i,1)=sharp(1); % статистика случайной стратегии
z(i,2)=max(sharp); % статистика лучшей стратегии
a=(X'*X)\(X'*y); r=X*a;
z(i,3)=mean®/std®; % статиситка лучшего портфеля
if isnan(z(i,3))
z(i,3)=0;
end
end
warning('on','all');
%% Изображение статистик по отношению к пределам
figure; r=z(:,2)./lim(:,2); mr=median®; histfit(r,30,'gev');
title(['Best Sharp Statistic median : ',num2str(mr)]);
xlabel('relation sharp to critical level'); ylabel('Frequency');
figure; r=z(:,1)./lim(:,1); mr=median®; histfit(r,30,'wbl');
title(['Random Sharp Statistic median : ',num2str(mr)]);
xlabel('relation sharp to critical level'); ylabel('Frequency');
figure; r=z(:,3)./lim(:,3); mr=median®; histfit(r,30,'gev');
title(['Best Portfolio Sharp Statistic median : ',num2str(mr)]);
xlabel('relation sharp to critical level'); ylabel('Frequency');
figure; r=z(:,2)./lim(:,2); plot(Narr,r,'.');
title(['Erorrs by effective dim']);
xlabel('Effective dim'); ylabel('relation sharp to critical level');
figure; plot(Narr*ones(1,3),lim,'.'); legend({'Random','Best','Portfolio'});
title(['Critical Levels by Effective Dim ']);
xlabel('Effective dim'); ylabel('Critical Levels');
end
% Генерация случайного набора стратегий размерности K, длинной L
function X=genRS(K,L)
Ne=ceil(rand(1,1)*K); % эффективная размерность задается случайно
A=randn(K,Ne); % случайная матрица смешивания
for i=1:K
A(i,:)=A(i,:)/sum(A(i,:).^2);
end
X=randn(L,Ne)*A';
end
Читайте на SMART-LAB:

МГКЛ на Smart-Lab & Cbonds PRO облигации 2.0 📍
Мы уже работаем на площадке и ждём вас на стенде МГКЛ — будем рады встрече и вопросам. 🕑 В 14:30 генеральный директор ПАО «МГКЛ» Алексей Лазутин выступит в зале «Писательский» на сессии...
28.02.2026











Ну не фига себе !
Не, ну не фига ж себе!!!