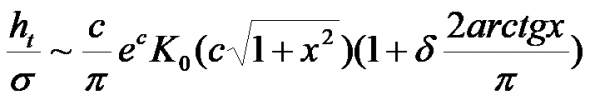О распределении приращений логарифмов H+L дней («давно я не брал в руки шашек»)

Это исследование я сделал под влиянием бурной дискуссии на форуме  о распределении «хвостов» приращений логарифмов цен, возникшей, казалось, на «пустом месте»: насколько корректны доверительные интервалы для оценок параметров линейной регрессии в альфа-бета модели?

Кроме указанной ссылки, дискуссия продолжилась в еще двух ветках: тут и тут.

Действительно, эти оценки в классическом случае строятся на основе центральной предельной теоремы для статистик оценок параметров линейной регрессии. Однако, как я уже писал на смартлабе, необходимым условием которой является скорость роста дисперсии суммы слагаемых как О(N), N – число слагаемых, а для быстрой сходимости в центральной области еще и требуется конечность абсолютного третьего момента любого слагаемого (если говорить о сходимости на всей прямой, включая «большие уклонения»,  то еще требуется  и конечность всех моментов отдельных слагаемых). Однако эти условия не выполняются для части распределений Парето и Стьюдента с полиномиальной скоростью убывания «хвостов» и поэтому для «хорошего» приближения суммы таких слагаемых нормальным законом требуется очень большое число испытаний, которых, как правило, в альфа-бета модели, построенной на дневных данных, нет. А значит традиционные методы построения доверительных интервалов для оценок параметров этой модели «не работают».

Собственно дискуссия в дальнейшем свелась к вопросу: распределены ли «хвосты» дневных приращений логарифмов цен по распределению Парето, т. е. c полиноминальным убыванием  О(х^-а) или мы имеем дело с экспоненциальным убыванием вида О(e^-axx^b), а>0, b-любое.

Первый результат основан на выделении отдельно «хвостов» и их приближении распределением Парето. При этом центральная область игнорируется, так как приблизить все распределение приращений логарифмов цен распределением Парето никак не получается. А что говорит в пользу второй гипотезы?

В своем видео с 21-й по 32-ю минуту я привожу рассуждения, на основании которых для  приращений логарифмов H+L  (h_t) дней будет иметь место распределение

со скоростью убывания «хвостов» О(e^-axx^-1/2), K₀-функция Макдональда.

Там же показана графическая «похожесть» этого распределения на распределение приращений логарифмов H+L  фьючерса на индекс РТС в 2005-2016 годах с выброшенным периодом «кризиса» с 17 сентября 2008-го по 28 февраля 2009-го. Однако никаких результатов статистических исследований не приведено. Восполним данный пробел на примере SPY на данных с 29.01.1993 по 24.05.2021.

Прежде чем переходить к результатам поясним, что из себя представляют приращения логарифмов H+L. В начале 2000-х я выяснил, что для РАО ЕЭС и Газпрома они имеют корреляцию больше 0,99 с приращениями логарифмов средневзвешенных цен дневок. Т. е. мы имеем дело с рядом приращений логарифмов средневзвешенных цен дневок, которые, ИМХО, более точно отражают картину дневных настроений, чем цены закрытия, т. е. цены в отдельный момент дня. А почему SPY, а не S&P500, история которого гораздо длиннее? Все дело в том, что в данных индекса не учитываются междневные гэпы из-за равенства открытие сегодня=закрытию вчера. И при наличии гэпа мы получаем, что в H или L могут присутствовать цены, которых вообще не было на торгах.

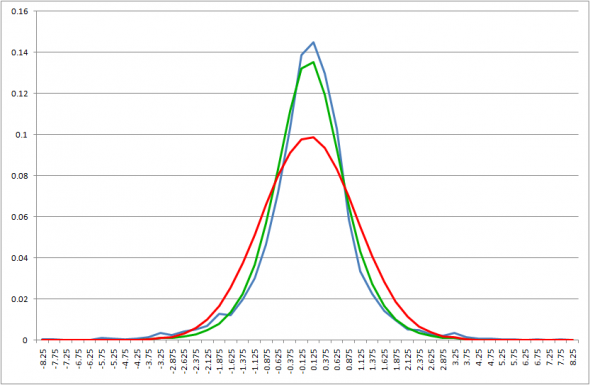
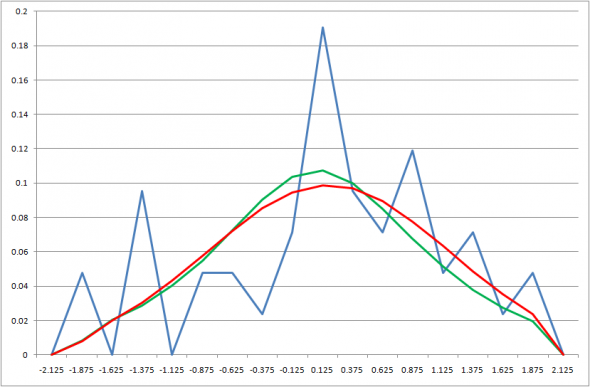
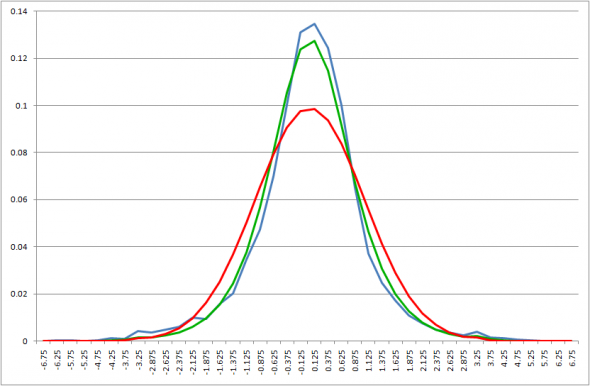
Возьмем весь ряд дневных приращений логарифмов и приблизим указанным распределением. Для плотностей получаем следующую картинку

Здесь и далее на графиках синим цветом обозначена гистограмма вероятностей распределения приращений логарифмов цен, нормированных среднеквадратичным отклонением, зеленым – аналогичная наиболее «близкая» гистограмма, для распределения с  вышеприведенной плотностью (обозначим ее Kо по аналогии с функцией Макдональда), а красным – та же гистограмма для нормального распределения с таким же средним, как у нормированных приращений логарифмов цен и дисперсией 1 (напомним, что дисперсия нормированного ряда приращений логарифмов тоже равна 1). Из этих гистограмм вероятностей получают функции распределения для сравнения по критерию Колмогорова.

Несмотря на визуальную «близость» зеленого и синего графика значение статистики Колмогорова отвергает гипотезу совпадения распределений с вероятностью ошибки первого рода  0.05 (см. сводную таблицу ниже: критическое значение статистики для вероятности ошибки первого рода  0.05 – 1.36). Итак, на всей истории получить приближение указанным распределением не удалось. Впрочем, и в вышеупомянутом видео я выбрасывал значения выборки для кризисного периода с 17 сентября 2008-го по 28 февраля 2009-го, специально оговорив, что в этот период, вероятней всего, данное распределение далеко от реальности.

А давайте по аналогии с факторным анализом из видео разобьем весь период на кластеры «волатильности» и посмотрим, что получается отдельно на каждом из кластеров.

Под  текущей «волатильностью», как и в случае факторного анализа, мы будем понимать максимум из двух величин:

— оценка сигма из упомянутого распределения по приращениям логарифмов H+L за 50 последних дней (меньше нельзя из-за ошибки оценки), т. е. в предположении, что параметры этого распределения были постоянны в эти 50 дней;

— СКО тех же приращений логарифмов за последние 10 дней.

Почему так? Вторая оценка очень неточная, но она позволяет быстро среагировать на рост волатильности. В то время как первая «увидит» реальный рост только  примерно через 25 торговых дней в силу сдвига «окна» расчета. Основной ошибкой такого расчета является то, что однодневный всплеск приращения логарифма можно принять за новый кластер более высокой волатильности в течении 9 дней, пока этот однодневный всплеск не уйдет из расчета. Но с точки зрения рисков — эта ошибка менее критична, чем ошибка пропустить реальный рост волатильности, которая при таком подходе менее вероятна.

И, кстати, для достаточно сильно разнесенных отрезков времени оценки сигма могут сильно отличаться, что свидетельствует о том, что этот параметр нестационарен. Однако больших «ступенек» (больше 25% от предыдущей величины) ни в одном из его выборочных рядов, разнесенных на 25 точек, нет. Что говорит об отсутствии больших «гэпов» (в разы) в этой величине и ее относительно «плавной» изменчивости. А это значит, что те же «хвосты» в исходной последовательности, либо серийны и появляются в результате постепенного нарастания «волатильности», либо единичны и крайне редки («черные лебеди»).

Вот какие у нас получились кластеры

О столбце «Без кризисов» чуть позже.

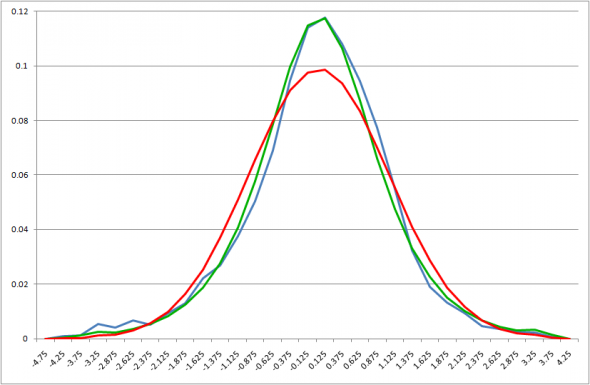
Начнем с кластера «низкой» волатильности

И мы сразу получаем по критерию Колмогорова, что гипотеза о совпадении распределений для нашего распределения не может быть отвергнута. Хотя гипотеза нормальности отвергается по этому критерию.

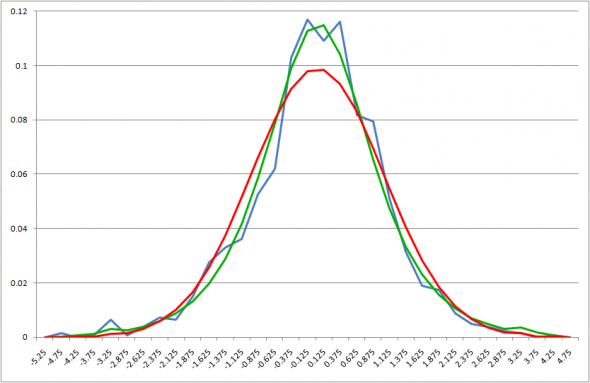
Еще лучше по тому же критерию получается для «средней» волатильности

Нормальное распределение, по прежнему, «вне игры».

И  для «высокой» «волатильности» критерий Колмогорова дает нам совпадение с нашим распределением

И даже совпадение с нормальным получается по этому критерию. Но надо учесть, что после нормировки мы получили совсем уж «вычурное» распределение, лежащее в диапазоне [-2,2]  и всего из 42-х точек. Кстати, «вычурность» этого распределения косвенно свидетельствует о том, что «сверхтяжелые хвосты» являются порождением «волатильности» в нашем определении.

Также отметим, что из 42-х последних точек, 40 попали на периоды 17.09.2008-15.12.2008 и 24.02.2020-10.04.2020, т. е. на «острые фазы кризисов».  Поэтому  последним шагом выбросим из данных эти периоды и посмотрим что получилось «Без кризисов»

И даже для этой выборки критерий Колмогорова дает нам совпадение с распределением Kо, хотя и «на тоненького». Ну а нормальное по прежнему «вне игры». Сводные данные по значениям статистики Колмогорова приведены в следующей таблице

Отметим также явную зависимость значений статистики Колмогорова от размаха колебаний нашей «волатильности» на выбранном периоде, что говорит о том, что для периодов с меньшим размахом, вероятней всего, приближение выборочного распределения распределением  Ко будет еще лучше.

Таким образом, высказанная в видео гипотеза о том, что приведенное распределение хорошо «объясняет» одномерное распределение приращений логарифмов цен  Н+L дневок вне периодов «острых фаз кризисов» полностью подтвердилась на SPY.