Критическая масса и критическое значение

Проведем небольшой тест — возьмем один случайный фьючерс, приращения которого представлены временным рядом случайных чисел, и набор случайных стратегий, представленный множеством N временных рядов случайных чисел (он же матрица признаков, фичей, пространство предикторов и т.д.) и попытаемся найти из этого большого набора тот признак, который будет лучше всего говорить нам когда покупать фьючерс, а когда продавать. Что это будет, мультипликатор P/E, фаза луны или MACD — не важно, главное чтобы на выходе получилась «идея» или, как ещё говорят, «грааль».


Хорошо известно, что случайная стратегия примененная к случайному инструменту даст случайное эквити, которое будет иметь гауссову плотность распределения коэффициента шарпа  с математическим ожиданием  0 и среднеквадратичным отклонением 


  

где L — число известных значений случайного фьючерса. 


Это означает, что достаточно большое множество случайных стратегий (или случайных признаков), примененных к случайному фьючерсу абсолютно случайным образом окажутся способными достаточно хорошо описать любое поведение случайного фьючерса (отклика) в бек-, форвард-, голкипер-, кросс-, спринт-  и всех прочих тестах… но только на истории.


Для того чтобы минимизировать риск отбора признака (стратегии) не имеющего никакой ценности в мат. статистике используется функция ошибок, связывающая вероятность реальной полезности признака и его прогностическую силу на исторических данных. 






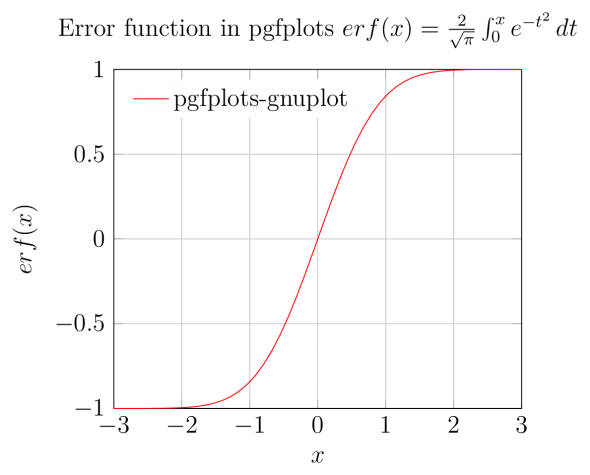
И обратная функция ошибок, позволяющая рассчитать критическое значение шарпа случайной эквити, при достижении которого мы можем утверждать, что с заданным уровнем доверительной вероятности альфа этот признак является полезным.


Таким образом, мы можем указать критерий отбора значимых признаков, при котором действительно значимыми окажутся более чем  из них :



где erfinv — обратная функция ошибок.


Но всё это хорошо, когда мы имеем одну стратегию и один признак. А если у нас их 100, или 1000, как это любят бигдата-сайентисты и различные количественные специалисты? 

Рискнем предположить, что ни один из N независимых случайных признаков, не покажет шарп выше заданного критерия с вероятностью  . Собственно, это всего лишь правило сложения вероятностей. Тогда критерий отбора признаков (стратегий) из признакового пространства размерностью N (набора стратегий из N стратегий) с доверительной вероятностью  будет задаваться так : 




Изобразим полученную зависимость для доверительной вероятности 90% и переменного числа признаков от 1 до 300:


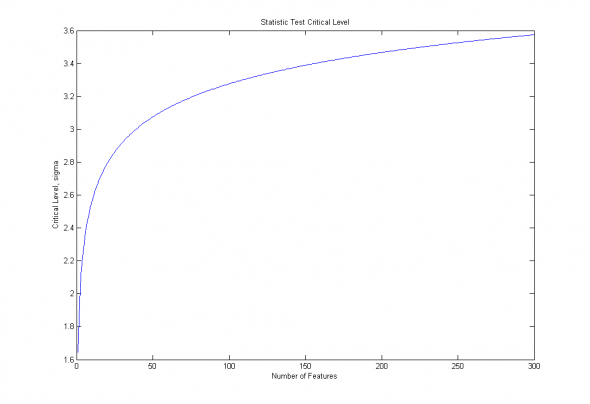
Рис. 1. Зависимость критического уровня от числа признаков, для доверительной вероятности 90%.


Особенно это опасно на данных небольшой размерности, когда незначительный рост размерности признакового пространства ведет к взрывному росту критических уровней статистической значимости.


Дополнительную сложность вызывает и само определение размерности признакового пространства в случае ненулевой коррелированности случайных признаков.  Мы не будем мудрствовать, и оценим эффективную размерность «на глаз», то есть в первом приближении : 



где С- корреляционная матрица случайных эквити, l-единичная вектор-строка.
Легко видеть, что при корреляции признаков 1, то есть когда, по-сути, мы имеем только один признак, — эффективная размерность стремится к 1, а при корреляции признаков равной нулю — к N.


Но мы, как настоящие дата-сайентисты, на этом не остановимся, а пойдем дальше, собрав из простых признаков-стратегий целый портфель. Легко показать, что портфель из стратегий взятых с весами  будет обладать шарпом :




где бетта — вектор строка весов признаков (стратегий), С — корреляционная матрица случайных эквити.


C другой стороны, перебирая все возможные портфели, мы будем варьировать не только знаменатель, но и числитель,  заставляя портфель перекладываться в менее прибыльные стратегии диверсифицирующие риски. Запишем приблизительное соотношение для оптимального портфеля, полученное из соображений пропорционального качеству взвешивания:





Следовательно, c учетом эффекта портфелизации, наш критический порог возрастает до:






Продемонстрируем справедливость оценок на примере авторегрессионных моделей броуновского движения :

MatLab side :

n=20; 
x=randn(1000,1); 
M=zeros(1000,n); 
for i=1:n; 
    M(:,i)=[zeros(i,1);x(1:end-i)]; 
end; 
a=(M'*M)\(M'*x); 
r=(M*a).*x; 

 
Mы будем искать медианное значение шарпа для AR(n) модели, такое которое с вероятностью 50% пройдет наш статистический тест:



Что для N=20 и бетта=1/N  даст пороговое значение :




Проведем тест из 1000 испытаний aвторегрессионных моделей порядка N=20, построенных на различных реализациях белого шума:


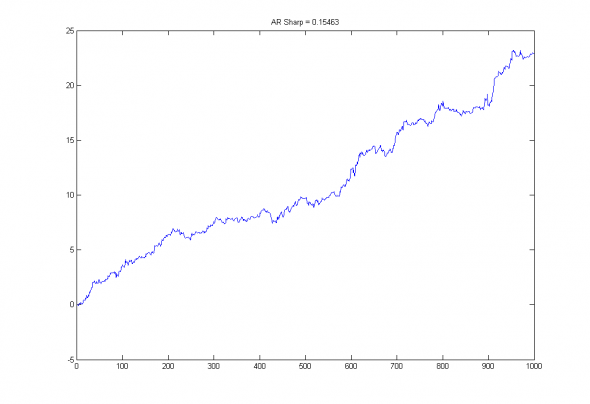
Рис2. Эквити и коэффициент шарпа случайной авторегрессионной модели порядка 20, построенной на белом шуме.



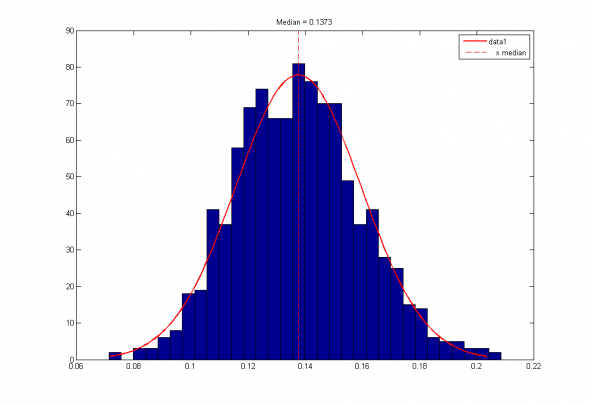
Рис 3. Распределение коэффициентов шарпов случайных авторегрессионных моделей порядка 20 и их медианное значение.


Видно, что полученная приблизительная оценка 0.1417 достаточно близка к эмпирическому значению 0.1373. 



Таким образом, получается, что реальные статистические пороги для портфельных методов и всех без исключения методов MachineLearning находятся многократно выше «классических» Z- и T- тестов.