За что я не люблю математиков, в том числе - АГ.
Резюме о методах «математического» анализа фондового рынка
Программа ProfitMaker начала разрабатываться с 1995 г. российской фирмой МП «КИТ» / «Кибернетика, Информатика, Технологии» /. Основным разработчиком пакета с самого первого этапа работ и по настоящее время является автор настоящей книги
Указанный пакет стоит особняком от существующего по состоянию на сегодняшний день программного обеспечения для финансового рынка. Это обусловлено, прежде всего, тем, что пакет даёт в руки инвестора не методы или же инструменты, которые он может использовать или нет, a ProfitMaker является самодостаточной «алгоритмической машиной (автоматом) для формирования потенциально возможной прибыли». Никаких других задач пакет не решает. Исключением из этого являются лишь чисто технические функции, выполняемые пакетом, такие, как работа с ретроспективными данными, визуализация результатов, поддержка баз данных и так далее.
Если ряд ранее рассмотренных «продвинутых» пакетов, например, таких, как Fortel Trade, PolyAnalyst и т. д. используют технологии «искусственного интеллекта» (нейронные сети, эволюционное программирование и генетические алгоритмы) для прогнозирования и принятия инвестиционных решений, то пакет ProfitMaker базируется в чистом виде на строгой математической теории оптимального управления динамическими системами. Корни этой методологии идут из области техники – авиационной, ракетно-космической, судостроения и т. д.
Применительно к финансовому рынку целью управления портфелем является выбор такой динамической последовательности инвестиционных решений (в виде пропорционального состава входящих в портфель финансовых инструментов), при реализации которой в течение всего планируемого периода будет обеспечено максимально возможное приращение стоимости портфеля. Реализация указанного управления обеспечит инвестору извлечение потенциально возможной для финансового рынка прибыли (дохода) на вложенные средства, если, конечно, инвестор будет придерживаться выдаваемых рекомендаций.
При торговле акциями и облигациями, безусловно, возможно проведение краткосрочных спекулятивных операций. Однако основная цель торговли указанными инструментами – это наращение стоимости портфеля в долгосрочном аспекте
Дальше бла бла бала ..............
Применительно к управляемому портфелю для рынка акций (см. рис. 9.5.) для результирующей эффективности управляемого портфеля будем иметь:

… бла бла бла
Главный фактор, который определяет потенциально достижимое значение эффективности управления портфелем ценных бумаг – это собственно рынок. Если курсы всех обращающихся на рынке ценных бумаг будут падать (их эффективности как расчётные величины также будут падать), при этом запрещается проведение операции «продажа без покрытия», то кроме убытков инвестора на подобном рынке ничего не ждёт.
В указанной ситуации инвестору надо просто уходить с данного рынка на тот рынок, где наблюдается рост котировок обращающихся на нём финансовых инструментов.
Каждый инвестор должен чётко понимать, что само по себе «оптимальное управление портфелем» – это лишь способ мобилизации скрытых резервов рынка.
Вывод
Математика способна наращивать портфель но жить за счет инвестиций — невозможно.
Автоследование за подобной стратегией кроме гарантированных убытков ни какого другого результата дать не может.
Ну нет у «математиков» Смарт лаб ни желания ни возможностей, исследовать именно структуру рыночного движения, его закономерность и последовательность.
Единственное желание — хапнуть чужое бабло при этом казаться — гениями торговли.
Математическая модель финансового рынка в непрерывном времени
Математическая модель финансового рынка может быть представлена в виде векторно-матричного дифференциального уравнения вида:
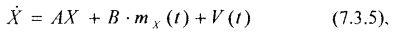
которое может быть решено при начальном условии:
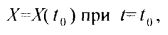
где:
— вектор X размерности (Nxl) по терминологии, принятой в теории управления динамическими системами, описывает «состояние» динамической системы и в этом смысле может быть назван вектором состояния финансового рынка;
— матрица коэффициентов А дифференциального уравнения (7.3.5) имеет размерность (NxN);
— матрица коэффициентов В имеет размерность (NxN), и её структура и значения коэффициентов выбираются таким образом, чтобы обеспечить условие астатизма воспроизведения векторной функции mx(t);
mx(t) – векторная функция, соответствующая математическому ожиданию векторного случайного процесса X(t);
V(t) – векторный случайный процесс белого шума (т. е. некоррелированный случайный процесс, имеющий корреляционную функцию в виде дельта-функции Дирака) с математическим ожиданием, равным нулю.
(оказывается «белый шум» это фикция! «Случайное блуждание цены» от демагогов со смарт лаб)
Известно, что векторное дифференциальное уравнения типа (7.3.5) эквивалентно системе скалярных дифференциальных уравнений. Применительно к обращению на рынке М финансовых инструментов соответствующее векторное дифференциальное уравнение можно представить в виде системы дифференциальных уравнений:
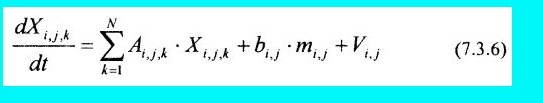
при начальных условиях:

где:
i = 1,…,M – порядковый номер финансового инструмента, обращающегося на финансовом рынке;
j = 1,…, L – порядковый номер производной соответствующего случайного процесса;
N = M + L;
Xi, j, k – случайный процесс, например, случайное значение текущей доходности i-го финансового инструмента или же значение его j-й производной.
Из выражения (7.3.6) видно, что каждый i-й финансовый инструмент описывается системой, состоящей из j дифференциальных уравнений 1-го порядка. Это объясняется тем, что фактически каждому i-му финансовому инструменту соответствует дифференциальное уравнение формирующего фильтра порядка L. Вместе с тем в канонической форме Коши дифференциальное уравнение порядка L может быть представлено как система, состоящая из L дифференциальных уравнений первого порядка. С учетом того, что общее число обращающихся на рынке финансовых инструментов мы приняли равным М, общая размерность N системы (7.3.6) равна N = M + L.
Дифференциальное уравнение вида (7.3.5) и соответствующая ему система (7.3.6), с учетом того факта, что в правой части указанных уравнений присутствует случайный процесс белого шума, называются стохастическими дифференциальными уравнениями.
Известно, что решение матричного дифференциального уравнения (7.3.5) с правой частью будет иметь вид:
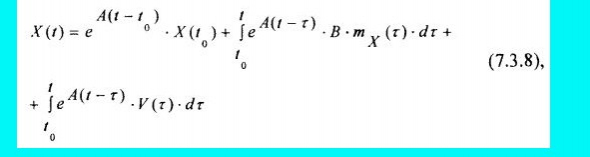
где eA(t – t0) – фундаментальная матрица решений дифференциального уравнения (7.3.5) в виде матричной экспоненты.
Переходя к математическим ожиданиям и учитывая, что математическое ожидание белого шума равно нулю, формула для вычисления математического ожидания векторного случайного процесса X(t), являющегося решением дифференциального уравнения (7.3.5), будет иметь вид:

Применительно к математическому ожиданию этот результат почти очевиден, т. к. по условию в правой части дифференциального уравнения (7.3.5) фигурирует математическое ожидание процесса X(t). Однако существенно большие трудности возникают при вычислении ковариационной функции случайного процесс X(t) через выражение (7.3.8), определяющее решение дифференциального уравнения (7.3.5). Все сложности начинаются с того, что в этом случае необходимо знать фундаментальное решение дифференциального уравнения (7.3.5) без правой части, т. е. необходимо знать фундаментальное решение однородного дифференциального уравнения вида:
бла бла бала
там куча формул но реально это теория и ни какого отношения именно к трейнигу не имеет.
вывод
Эффективность математики только в поиске закономерности рыночного движения — паттернов которые способны реально материализовать вашу прибыль.
Вы считаете что Ваши математики что то новое внесут в реальность трейдинга?
НИЧЕГО! просто слямзять уже известное и добавят новые буквы в очередной — бесполезной формуле. (равносильно волновой теории рынка)














«Случайное блуждание цены» от демагогов со смарт лаб
"Доктора наук, профессора и тд, глядя на мои наработки только гривой машут и по полчаса в себя придти не могут от увиденного, ."
видел я и не раз и не два как вытягиваются лица этих «гениев», когда они оценивают увиденное.
«По твоей системе я обе тенденции веду и на месяцах и на неделях и на днях, но секрет моделей пока не раскрыл, те модели которые у тебя в примерах приведены, на мои не больно то похожи, хотя все равно, хотя бы их понимание дает подсказки и неплохие.»
У человека почти год! основные принципы работы моих зигзагов, но «мелочи» не позволяют ему получить общую картину рыночного ценообразования. Потому я спокоен, если даже есть приблизительно — направление, то копаться ему еще много, много лет и не факт что будет какой то толк!