Модель Курбаковского, сглаживание и нормировка

Большое спасибо Виталию Курбаковскому, что опубликовал свою обобщенную модель ценообразования опционов (1, 2, 3, 4, 5). Давно хотелось подобную модель, с минимум параметров, физический смысл которых был бы более-менее понятен. Чтобы можно было осознано свои параметры модели задавать, а не подгоняться под рынок и слепо за ним идти. Модель, которую использует биржа (с шестью параметрами ABCDES) под такой запрос не подходит. Попробуй там пойми, все ли шесть параметров сейчас имеют справедливые и оправданные значения, или с каким-то из параметров можно поспорить. И слишком уж она гибкая. Бывало смотришь — выскочила какая-то котировка за модель, только соберешься по ней ударить, а программа параметры модели подкорректировала и услужливо изогнула кривую с учетом новой котировки. И то, что только что
выбивалось за модель, стало ей соответствовать. Пробовал еще модель китайской улыбки, там и параметров поменьше и смысл у них попонятнее, но очень уж плохо она подгоняется под рынок. И тут, на счастье, Виталий поделился своей моделью и все подробно объяснил. Реализовал у себя и оказалось — то что надо. И в рынок хорошо вписывается, и параметры имеет понятные.

Добавил в модель немного отсебятины. Хочу поделится, может кому тоже пригодится, а может кто покритикует/посоветует чего. Проблема в том, что если считать дельту просто по формуле, то получается скачок при переходе через ЦС. И если пересчитать цены в улыбку IV, то получается линейная галочка. С одной стороны — улыбка IV вроде как бессмысленная сущность и являет собой просто набор поправочных коэф-тов. Но с другой стороны все таки нет-нет, да и посмотришь на улыбку. И как-то не по себе, когда вместо привычной плавной параболы видишь угловатую галочку. Виталий написал, как сглаживать дельты, но как сглаживать сами цены пока не ответил. Стал кумекать — как бы попроще все сгладить без лишних вычислений и придумалось такое:

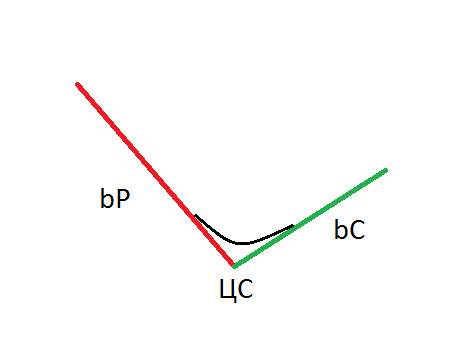
Решил просто сгладить переход между bP и bC с помощью ф-ции Tanh (гиперболический тангенс). Причем коэф-т сглаживания (широко или узко сглаживать) стал нормировать на время и на относительное расстояние страйка до ЦС. Заменил везде, где у Курбаковского:

b = bc
If S < x Then b = bp

на такое (это уже Паскаль):

b := bP + (bC — bP) * (1+Tanh(Ln(S/x)/Sqrt(T)/CoefSmooth))/2

И получилось замечательно. Улыбки стали на загляденье, с плавными донышками. Ушел скачок в дельтах. И главное: один и тот же коэф-т сглаживания (CoefSmooth) одинаково хорошо подходит для разных календарных серий. И даже у разных БА довольно близок. Например, для Ri подошел 0.05, а для Si 0.04.

Обрадовавшись этому результату, решил попробовать еще нормировать параметры bP и bC. Чтобы они тоже не зависели от времени до экспирации. Вот история этих параметров (для RTS-12.19M191219):

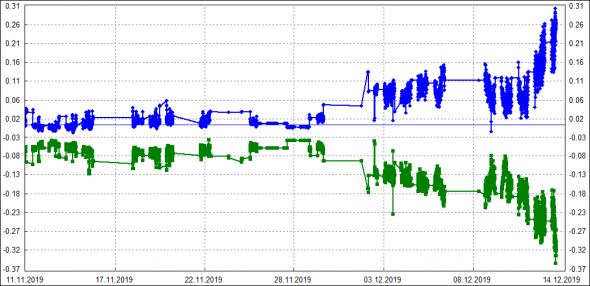
Попробовал сначала в лоб и везде в формулах заменил (S-x), на Ln(S/x)/Sqrt(T). Т.е. как-бы заменил абсолютное центрирование на относительное, да еще и на время нормировал. Но не тут то было, программа не смогла подобрать параметры модели, чтобы теорцены подходили под рынок. Возможно, при такой нормировке и mI нужно считать как-то по другому. Как — не придумал. Решил просто подобрать ф-ции под историю bB/bC. Видно, что они изменяются симметрично. Ось симметрии, кстати, на уровне -0.03. А по моим прикидкам, на Ri параметр bK можно как раз оценить около -0.03:

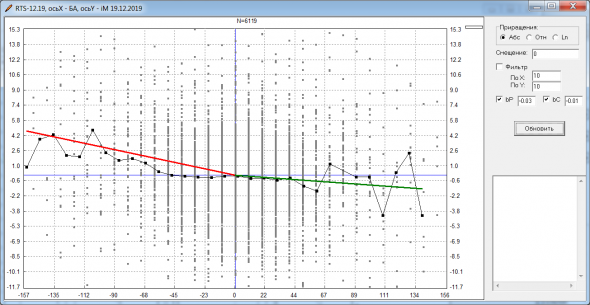
Решил, что это не спроста и неслучайное совпадение. Виталий же писал, что в теории должно было быть: bP=bC=bK. А тут получается, что оба коэф-та и bP и bC берут свое начало с bK, и потом со временем симметрично разъезжаются. Приготовился к долгим поискам, но уже с третьей попытки подобрал простые формулы:
bP = bK — 1/T
bC = bK + 1/T

Вот как они накладываются на историю:

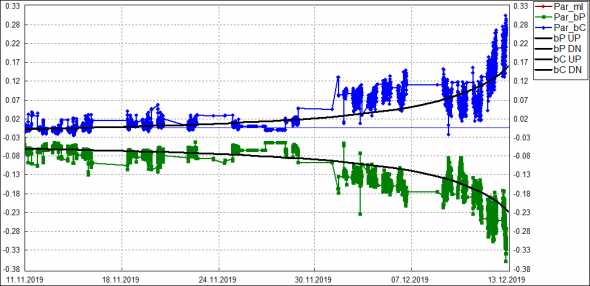
Наверное, не очень хорошо вот так, не понимая сути, просто методом тыка подбирать коэф-ты и зависимости. Но зато теперь вместо модели с тремя динамическими параметрами (mI, bP, bC) + одним статическим (bK), получаем модель только с одним динамическим параметром (mI) и двумя статическими (bK и коэф-т сглаживания). Фактически, теперь можно торговать все опционы (все страйки всех календарных серий на один БА) с помощью только одного параметра mI. Ну классно же?! :)