28 августа 2019, 04:47
Обобщённый подход к диверсификации рисков
Дополнение к серии «Портфельная оптимизация как бустинг на слабых моделях»
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
)
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
Иными словами, вследствие нелинейности самой задачи, ошибки в определении статистической взаимосвязи различных активов не уничтожаются суммированием( как это происходит при подсчёте средних), а, наоборот, усиливаются функцией min / max и приводят к абсолютно непредсказуемым, хаотичным результатам. Что, в свою очередь, означает не только не-оптимальные инвестиционные решения, но и большой объём «паразитного» оборота, повторяющего случайные блуждания портфеля, требующего повышенной ликвидности и разоряющего инвестора комиссиями биржи.
Для решения этих нелинейных проблем возможно использовать простые линейные алгоритмы, позаимствованные из методов статистической регрессии и известные как регуляризация (Тихонова, Лассо и пр.). Смысл этих методов состоит в том, чтобы перевести задачу из области нелинейности, связанной с поиском минимума корреляций, в некоторую область линейности, умышленно стимулировав широкодиверсифицированные инвестиции по всему рынку (без оглядки на корреляцию). Достигается это путём регуляризации или усадки матриц :
Cov_{basis})
где — Cov — ковариационная матрица используемая в задаче, Cov(sample) — выборочная ковариация, Cov(basis) — базисная ковариация, ламбда — параметр регуляризации, подбираемый бэк-тестом или выбираемый на каждом шаге исходя из общих характеристик матриц.
Видно, что при ламбда = 0, задача вырождается и приобретает характер задачи в некоторых априорных предположениях о характере взаимосвязи активов, заданных матрицей Cov(basis).
Этими априорными предположениями (базисом ковариации) могут выступать :
Забегая вперёд, отметим, что, в целом, результаты наших испытаний по этим методам соответствуют результатам сторонних авторов.
Второй подход, предложенный Р.Энглом (Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH,
2001), заключается использовании динамических моделей корреляций (DCC) c использованием различных сглаживающих фильтров (например, фильтра Калмана или скользящей средней). В этом подходе используемая ковариационная матрица рассчитывается как:
Cov_{basis})
Это обобщённое уравнение совмещает в себе оба подхода — при бетта = 1/n и альфа+бетта =1, оно вырождается в уравнение усадки матриц, рассмотренное ранее, а при других значениях дополняет усадку фильтром Калмана ( в зависимости от соотношений альфа и бетта) и динамической моделью ковариации, зависящей от коэффициентов вектора бетта.
В качестве исходных данных для OOS теста моделей мы взяли фондовый рынок США, представленный 64 активами за период с 08.09.11 до 11.09.18. В качестве базовой модели оценки доходности — математическое ожидание IS выборки, рисков — модель на основе Bipower Variation. То есть самый простой и из всех возможных методов. Период наблюдений — 120 дней, минимальный из всех эффективных периодов, период инвестирования — 60 дней.
Апостериорный анализ возможностей портфельного инвестирования утверждает, что на выбранном интервале времени достижимы портфели с годовым коэффициентом Шарпа 1.32, в то же время базовая модель без преобразования ковариационных матриц достигает уровня качества не более чем 0.95.
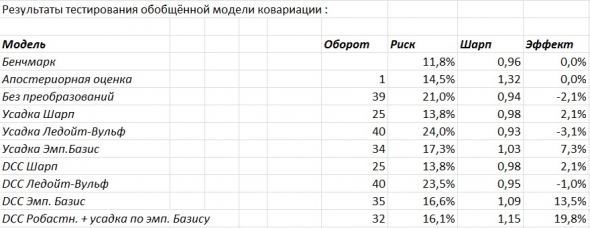
Таблица результатов тестов.
Из таблицы видно, что DCC (dynamic conditional covariation) модели в среднем выигрывают у CCC (constant conditional covariation) моделей. При этом стандартные процедуры усадки работают слабо удовлетворительно и почти не имеют эффекта. Модель Шарпа, при этом, превосходит модель Ледойт-Вульфа, вероятно из-за некоторой, присущей ей дискретности, связанной с не завышением ковариаций слабо коррелированных активов и слабым снижением ковариации сильно коррелированных активов. Устранить этот недостаток Ледойт-Вульф модели с сохранением всех её преимуществ (в качестве априорного предположения вводится ненулевая корреляция, что лучше соответствует действительности) позволяет более сложная факторная модель (Principal Component Analysis), разделяющая активы на группы слабо и сильно коррелированных с текущими движущими рынок факторами.
- Обобщённая проблема
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
Иными словами, вследствие нелинейности самой задачи, ошибки в определении статистической взаимосвязи различных активов не уничтожаются суммированием( как это происходит при подсчёте средних), а, наоборот, усиливаются функцией min / max и приводят к абсолютно непредсказуемым, хаотичным результатам. Что, в свою очередь, означает не только не-оптимальные инвестиционные решения, но и большой объём «паразитного» оборота, повторяющего случайные блуждания портфеля, требующего повышенной ликвидности и разоряющего инвестора комиссиями биржи.
- Усадка ковариационной матрицы (Shrinkage)
Для решения этих нелинейных проблем возможно использовать простые линейные алгоритмы, позаимствованные из методов статистической регрессии и известные как регуляризация (Тихонова, Лассо и пр.). Смысл этих методов состоит в том, чтобы перевести задачу из области нелинейности, связанной с поиском минимума корреляций, в некоторую область линейности, умышленно стимулировав широкодиверсифицированные инвестиции по всему рынку (без оглядки на корреляцию). Достигается это путём регуляризации или усадки матриц :
где — Cov — ковариационная матрица используемая в задаче, Cov(sample) — выборочная ковариация, Cov(basis) — базисная ковариация, ламбда — параметр регуляризации, подбираемый бэк-тестом или выбираемый на каждом шаге исходя из общих характеристик матриц.
Видно, что при ламбда = 0, задача вырождается и приобретает характер задачи в некоторых априорных предположениях о характере взаимосвязи активов, заданных матрицей Cov(basis).
Этими априорными предположениями (базисом ковариации) могут выступать :
- Предположение о нулевой корреляции активов (Sharpe,1963)
- Предположение о некотором общем уровне взаимосвязи для всех активов (Ledoit & Wolf,2003)
- Отсутствие каких либо априорных предположений и использование эмпирического базиса в целях усадки (PCA, задача настоящей работы)
Забегая вперёд, отметим, что, в целом, результаты наших испытаний по этим методам соответствуют результатам сторонних авторов.
- Динамические модели условных корреляций и функции сглаживания
Второй подход, предложенный Р.Энглом (Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH,
2001), заключается использовании динамических моделей корреляций (DCC) c использованием различных сглаживающих фильтров (например, фильтра Калмана или скользящей средней). В этом подходе используемая ковариационная матрица рассчитывается как:
Это обобщённое уравнение совмещает в себе оба подхода — при бетта = 1/n и альфа+бетта =1, оно вырождается в уравнение усадки матриц, рассмотренное ранее, а при других значениях дополняет усадку фильтром Калмана ( в зависимости от соотношений альфа и бетта) и динамической моделью ковариации, зависящей от коэффициентов вектора бетта.
- Оценка качества моделей при решении тестовой проблемы
В качестве исходных данных для OOS теста моделей мы взяли фондовый рынок США, представленный 64 активами за период с 08.09.11 до 11.09.18. В качестве базовой модели оценки доходности — математическое ожидание IS выборки, рисков — модель на основе Bipower Variation. То есть самый простой и из всех возможных методов. Период наблюдений — 120 дней, минимальный из всех эффективных периодов, период инвестирования — 60 дней.
Апостериорный анализ возможностей портфельного инвестирования утверждает, что на выбранном интервале времени достижимы портфели с годовым коэффициентом Шарпа 1.32, в то же время базовая модель без преобразования ковариационных матриц достигает уровня качества не более чем 0.95.

Таблица результатов тестов.
Из таблицы видно, что DCC (dynamic conditional covariation) модели в среднем выигрывают у CCC (constant conditional covariation) моделей. При этом стандартные процедуры усадки работают слабо удовлетворительно и почти не имеют эффекта. Модель Шарпа, при этом, превосходит модель Ледойт-Вульфа, вероятно из-за некоторой, присущей ей дискретности, связанной с не завышением ковариаций слабо коррелированных активов и слабым снижением ковариации сильно коррелированных активов. Устранить этот недостаток Ледойт-Вульф модели с сохранением всех её преимуществ (в качестве априорного предположения вводится ненулевая корреляция, что лучше соответствует действительности) позволяет более сложная факторная модель (Principal Component Analysis), разделяющая активы на группы слабо и сильно коррелированных с текущими движущими рынок факторами.
Читайте на SMART-LAB:

МГКЛ на Smart-Lab & Cbonds PRO облигации 2.0 📍
Мы уже работаем на площадке и ждём вас на стенде МГКЛ — будем рады встрече и вопросам. 🕑 В 14:30 генеральный директор ПАО «МГКЛ» Алексей Лазутин выступит в зале «Писательский» на сессии...
28.02.2026











1. Не совсем понятна задача t-testa.
Разница, безусловно есть и очень сильная. Шарп давит доходность превращая портфель в индекс (16%). Вульф оставляет высокую доходность, но не диверсифицирует риски (23%), PCA сохраняет доходность (около 20%) с хорошим подавлением дисперсии. Поэтому да — значимая разница есть.
2. Ни на каком. Для того, чтобы получить «честный OOS» использую только непараметрические фильтры. Параметр длинны выборки не подбирался. За исключением того, что был выбран минимальный (самый тяжёлый для прогнозирования) из всех статистически значимых (эффективных) периодов. На периодах в 60 дней и менее, в силу случайности динамики ВР, уже невозможно выделить среднюю, ковариацию и т.д.
3. Начинал с BrokenStick, но пришлось её ослабить, так как «сломанная трость» выделяла только 1 Г.К. после… некоторой модернизации в среднем PCA оставило 4 компоненты. (на глаз я бы оставил только 3).
Это самый простой в реализации автомат. Для проверки качества методов — вполне достаточно.
Это всегда приветствуется!
1.
Сейчас я вам ничего не отвечу, но за подсказку — спасибо.
2.
Какими только извращениями на этом пути я не занимался. Результат — так себе. В итоге пришёл к выводу, что квадратичная оценка ковариаций одна из лучших. Регуляризую, естественно, корреляционную матрицу, а потом совершаю обратный пересчёт.
Предположим, что вы имеете две модели с доходностью 10% и 10.01% — разница не значимая, но какую модель вы выберете?
В лучшем случае, можно выбрать комбинацию из двух. Но при этом ответить на вопрос какая модель однозначно лучше вы не можете. Единственное, что вы можете указать, что вероятность того, что модель с бОльшей доходностью лучше — больше, вот и всё.
Поэтому применять t-test для того, чтобы найти существенную разницу между моделями не вижу особого смысла, потому как построить две модели (с разницей в 1 метод) с явным стат. преимуществом как-то не получается. За 5-10 модернизаций появляется ощутимое различие (раза в 2 по Шарпу) и тут уже можно о чём-то говорить, но применительно к одному дополнению типа Shrinkage — нет.