07 ноября 2020, 09:23
Непредсказуемость риска
Привычное управление капиталом предполагает привычные подходы к риску, разработанные ещё для детерминированных финансовых инструментов, таких как акции и облигации :
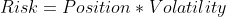
И даже если управляющий ошибется при расчете риска, то эта ошибка для риск-менеджмента в большинстве случаев не станет критичной :
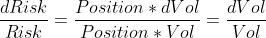
Другими словами, относительная ошибка контроля риска пропорциональна относительной ошибке оценки волатильности и на практике составляет не столь существенную величину — около 20%.
Но для стохастических финансовых инструментов, которые с вероятностью p превращаются в детерминированный финансовый инструмент, а с вероятностью (1-p) растворяются (например, это могут быть опционы), риск уже должен быть записан иначе :
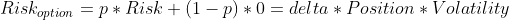
Теперь риск инвестиций в финансовый актив зависит не только от волатильности и вложенного капитала, как было ранее, но ещё и от некоторой неконтролируемой переменной дельта, характеризующей чувствительность опциона к изменению цен базового актива или использованное «плечо». Таким образом, получается, что инвестиции в опционы это не просто инвестиции, а инвестиции со стохастическим плечом и неконтролируемым риском.
В этом случае относительная ошибка оценки риска составит:
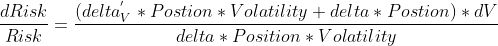
Или, с учётом того, что риск опционных конструкций в некотором приближении пропорционален их стоимости, запишем :
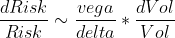
Теперь рассмотрим зависимость случайных величин delta и vega от случайного страйка на недельных опционах RI :
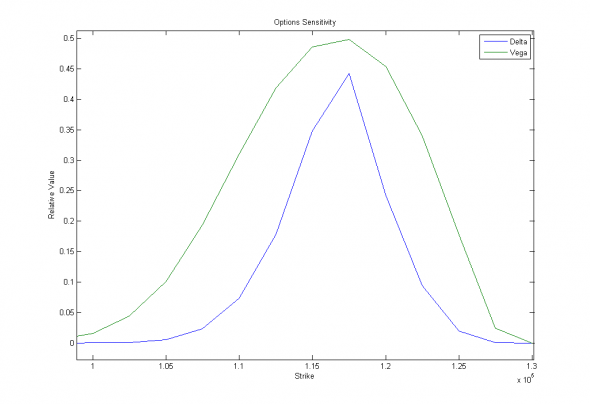
Иллюстрация. Дельта (вероятность превращения во фьючерс) и Вега (чувствительность премии к волатильности) недельных опционов RI в зависимости от страйка при цене базового актива 116 640 пунктов.
И их отношение, характеризующее коэффициент пропорциональности между относительной ошибкой контроля рисков и относительной ошибкой оценки волатильности:
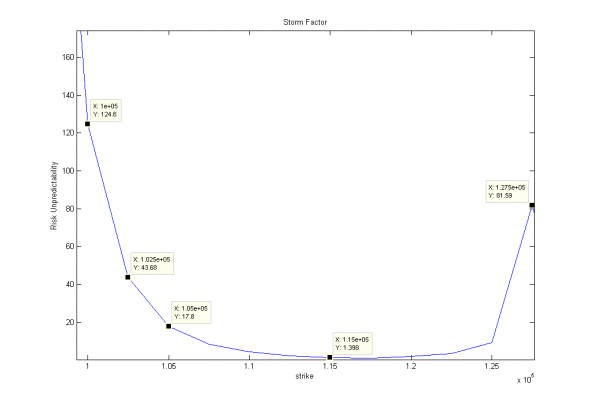
Иллюстрация. Возможные превышения рисков управляющим при относительной ошибке оценивания волатильности 1.
Видно, что даже если предположить максимальную ошибку оценки волатильности 50% (что вполне вероятно), то при продаже или покупке опционных «краев» можно легко превысить расчетные риски в 8 (105 000), 20 (102 500) и даже 60 раз (100 000). О каком контроле рисков здесь вообще может идти речь?
Ранее, симуляционное моделирование контроля рисков при торговле опционами показало схожие результаты:
Иллюстрация. Реализованный риск при торговле опционами на индекс SP500, при ограничении риск-контроля 3 (превышение в 40 раз).
Опасность данного эффекта в том, что он приводит к редким, но фатальным просчетам, объясняющим неприменимость классических критериев Sharp и MDD при оценке управления портфелем опционов.
Читайте на SMART-LAB:

Итоги первичных размещений ВДО и некоторых розничных выпусков на 2 марта 2026 г.
Следите за нашими новостями в удобном формате: Telegram , Youtube , RuTube, Smart-lab , ВКонтакте , Сайт
02.03.2026

Режим risk-off: почему удар по Ирану усилил доллар, но не поддержал облигации
Понедельник начался с довольного нетипичного режима риск-офф: доллар укрепляется по всему рынку, мировые акции снижаются, золото выросло более чем на 4%, Brent в моменте подскакивал на 13%....
02.03.2026












то есть если покупать/продавать опционы на ЦС риски под контролем будут и все ок?
Я в прошлом так не смог осилить задачу определения и управления этой неконтролируемой переменной дельта. Единственным решением (понимаю, что неидеальным) стала синтетика.