21 июня 2020, 20:34
Случайности в волатильности и эффективные оценки
Используя простые модели волатильности, рассчитанные по ценам закрытия (Close-to-Close vol.) мы неизбежно сталкиваемся с рыночным шумом, смещающим наши оценки далеко её от истинного или асимптотического значения. Мы могли бы измерять волатильность как-то иначе, например по модели Паркинсона (High-to-Low 1980), но столкнулись бы с той же проблемой.
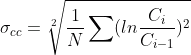
1.1 — Close to Close log-volatility estimation
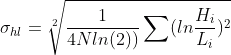
1.2 Parkinson (High to Low) log-volatility estimation
Эти две оценки волатильности, хоть и являются случайными числами, но используют совершенно различную информацию ({Close} и {High,Low}). На первый взгляд ничего интересного, но Garman и Klass, воспользовавшись теоремой Цыбенко (Neural Net approximation), решили построить на базе этих двух случайных чисел, новое, более эффективное случайное число, собрав, всего-навсего, из них простой, непараметрический портфель.
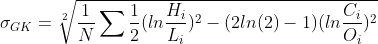
1.3 Garman and Klass log-volatility estimation
Математики заявляют, что этот портфель в семь с половиной раз эффективнее старой-доброй Close-to-Close.
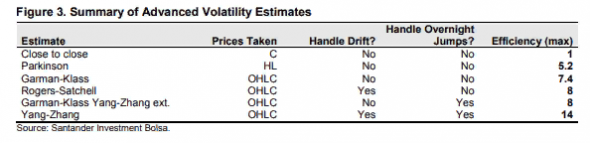
Сравнительная эффективность методов оценки волатильности.
Ну вот это мы сейчас и проверим!
Возьмем Gaussian Normal Standart Noise, построим из него Japan Candle graph, и начнем к нему EWMA 10 estimation применять!
Matlab:
q=10000; w=10; x=randn(q,w)/w^0.5;
x=cumsum(x,2); OLHC=zeros(q,4);
for i=1:q;
OLHC(i,2)=min([0,x(i,:)]);
OLHC(i,3)=max([0,x(i,:)]);
OLHC(i,4)=x(i,w);
end;
clear x q w i;
>> OLHCs=OLHC+cumsum([0;OLHC(1:end-1,4)])*ones(1,4);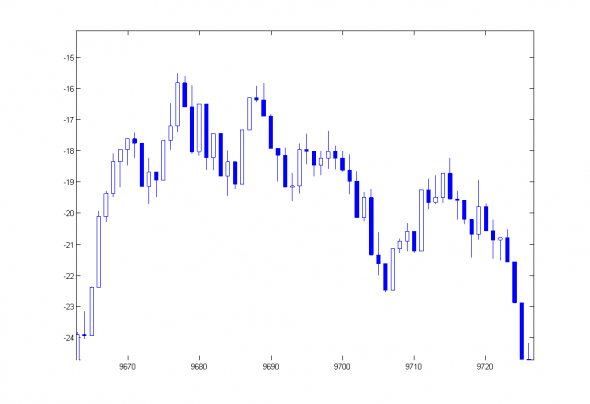
Matlab Random Candle Noise with truth unit volatility = 1.
Matlab:
volcc=tsmovavg(OLHC(:,4).^2,'e',10,1).^0.5; volcc(1:10)=[]; volhl=(1/4/log(2))^0.5*tsmovavg((OLHC(:,3)-OLHC(:,2)).^2,'e',10,1).^0.5; volhl(1:10)=[]; volhl=volhl/mean(volhl); volgk=tsmovavg( 0.5*(OLHC(:,3)-OLHC(:,2)).^2 - (2*log(2)-1)*OLHC(:,4).^2 ,'e',10,1).^0.5; volgk(1:10)=[]; volgk=volgk/mean(volgk);
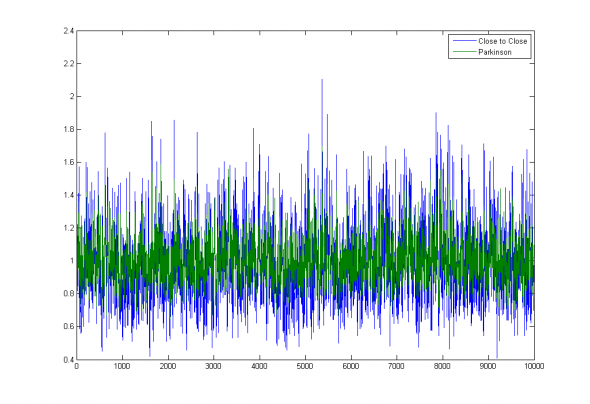
Close-to-Close estimation error = 0.22, Parkinson estimation error = 0.13;
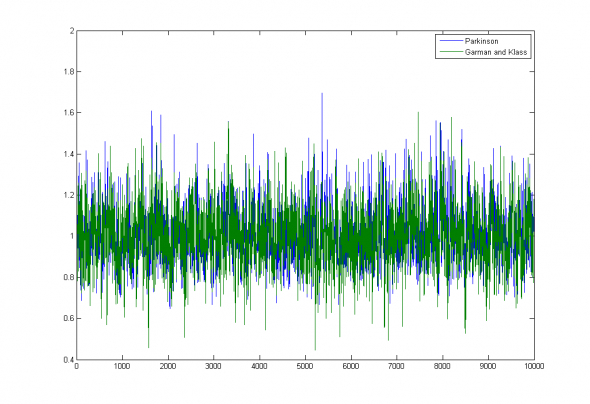
Parkinson estimation error = 0.13, Garman and Klass estimation error = 0.135; (преимущество Garman and Klass наблюдается на окнах >20)
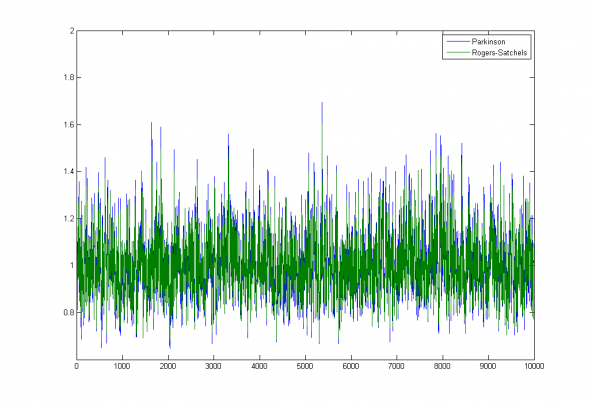
Parkinson estimation error = 0.13, Rogers-Satchell estimation error = 0.12;
Неправильные какие-то математики получились, ненормированные. Надо опять к Бабе Яге идти, она эти волатильности… ух как умеет!
10:30
etnos care, ЦИПСО, наверное. «Невидимый боец невидимого фронта»
На т-банк что-то пришло, по сумме похожее на Европлан. Пока не появилась операция в брокере, но больше вроде нечему. Разве можно так быстро?
Леонид Хазанов, напоминает предвыборные обещания, которые конечно же всегда реализуются.)))))
10:29
Денис Сёмочкин,
Тогда не было маркетплейсов, самокатов, яндекс лавок, вкусвилов и вообще поколение Зумеров сейчас на подходе. Они вообще готовить не будут. Будут заказывать еду в Яндекс-Дилав...
📉 Акции Headhunter начали торги -20% после отсечки мегадивиденда
Авто-репост. Читать в блоге >>>
Начались рождественские сралли :)
evem, не удивительно, всё ради налоговой оптимизации
smart-lab.ru/blog/1074948.php
Неужели на свете есть такие дураки, которые это дурьмо покупают, особено глядя на график сверху?
Трамп заявил, что может отменить решение Байдена об ударах по России дальнобойным оружием
Трамп намерен поддерживать контакты с Путиным и Зеленским для решения украинского кризиса. Рубль и акции нем...
10:26
Андрей Хохрин, что-то ссылка подозрительная какая-то у вас
youtu.be/Z7_Tc1mPXLk
Вы меня переплюнули, снимаю шляпу! Браво!
Например у нас есть последовательность 1, 2, 3, 4 — как видно, смещение равно 1, т.е. максимальная разница между этими величинами. Как её посчитать? Если всё сложить и разделить на количество, получим 2.5 — не круто, это нам не о чем не говорит (хотя это нам говорит о мат. ожидании).
Но нам интересно получить разброс. Если просто взять каждое значение и сравнить его с МО, сложить и получить среднее, получим 1 — что есть среднее абсолютное отклонение (MAD). Но это значение выходит не очень информативным, т.к. его можно получить из разных величин с гораздо меньшим разбросом, например (1, 1, 2 = 1 или 1.5, 0.5, 0.5, 1.5 = 1 и т.д.).
Чтобы исправить это мы и используем квадраты (СКО). Так мы получаем разницу МО минус значение, в квадрате, потом сумму квадратов делим на количество и извлекаем корень. Итого имеем относительно точное значение разброса. Для 1, 2, 3, 4 получим 1.25. Не 1, но близко. Это и есть волатильность.
(в случае чего, на истину в первой инстанции не претендую, сохраняю право на ошибку)
написал внизу про волатильность.
ЗЫ вообще, всю обработку реал-там инфы в прямоугольных окнах давно не делают.
В обработке сигналов так не делают. А они, в большинстве своем, стационарны.
Увеличьте выборку, и все дела.
Получается примерно так.
Это индикаторы волатильности, но не совсем то, что вам надо.
Зы. А чтоб не оч увеличивался там надо окно, что-то типа e^(-x^2), и можно начать где-то с середины интервала.
Зы2 Или даже куском синуса окно завершить.
Вы так говорите, как буд-то сумма x(i) это не есть самая простая линейная (или даже нулевая) аппроксимация, лишь волей случая совпадающая с МОЖ. А какая-нибудь сумма S1(x) и S2(x) не есть какая-то нейронная сеть на каких нибудь… квадратичных нейронах.
какое-то самозапутывание… и чем займней выглядит тем больше видимо в него веришь и запутываешься :)))
Существует два определения:
1) Волатильность рыночная, она же историческая, она же реальная — сие есть расчет или прикидка на глаз амплитуды колебаний конкретного инструмента. Акция волатильная — значит хорошо ходит, можно делать деньги. Акция сильно волатильная — значит шлак, который делает резкие значительные и плохо просчитываемые движения. Из-за повышенного риска сильную волитильность (амплитуды на графике) рекомендутся избегать.
Пункт 1) и 2) никак не связаны. Хотя слово «волатильность» в них одно и то же.
2) Волатильность вменённая, она же подразумеваемая, она же надуманная, она же предполагаемая, она же будущая волатильность, она же IV (ай-ви), она же сигма == это аналог выражения «цена опционов», аналог выражения «премия опционов», аналог выражения «риск опционов».
Левая и правая часть этого смыслового предложения (до и после знака ==) железно связывается формулой Блека-Шоулза. Это единственное предназначение формулы. Для этой формулы мы используем или цену опциона (реальную или придуманную) и получаем волатильность в процентах. Или задаем волатильность в процентах (реальную или придуманную) и получаем цену опционов. Поэтому тут стоит знак равенства. Чаще придуманную, чем реальную. Потому что цены для опционов мы берем «из общих соображений», с потолка. И кто-то на них соглашается, проходит сделка. Вот и всё.
Выражение трейдера с торгового деска «Я продал волатильность» означает, что он выставил опционы на продажу по хорошей спекулятивной цене, взятой с потолка, и у него их купили.
Выражение «Я продал волатильность» (в опционах, для акций не катит) равносильно «Я двинул лохам опционы по хорошей цене. Включаем счетчик временного распада и съедаем риск на завтрак!»
Обычное словоблудие. Ничего сложного.
человек выше спрашивал