Язык дракона и танец волатильности

«Настоящее образование включает умение хорошо петь и танцевать».  Платон.



Коллега ch5oh задал парадоксальный, на первый взгляд, вопрос: «как продавая дорого то, что стоит дешево, можно ещё и умудриться проиграть?»
Однако парадоксально он выглядит лишь до тех пор, пока мы остаёмся в рамках косной метафизики, не желающей, и не склонной к диалектическому танцу. 

Для сравнения этих двух подходов — метафизики и диалектики — мы будем рассчитывать Нэш-равновесные цены двух недельных опционов (STO) и моделировать игру покупателя и продавца. В первом случае мы будем исходить из постоянства (авторегрессии) волатильности, пользуясь исключительно текущей HV,  а во втором — из её танца (mean-reverse AR), о котором, как нам кажется, мы знаем чуть более, чем ничего.


* То, что волатильность представляет из себя mean-reverse процесс, подобный движению Орнштейн-Уленбека, неоднократно было показано Дмитрием Новиковым , Евгением Логуновым , и Котом-Бегемотом (например в статьях Авторегрессия волатильности и Путешествие по морю штормов )





Для примера возьмём какой-нибудь простой базовый актив, например индекс американских акций SP500 и построим сначала простую HV модель :



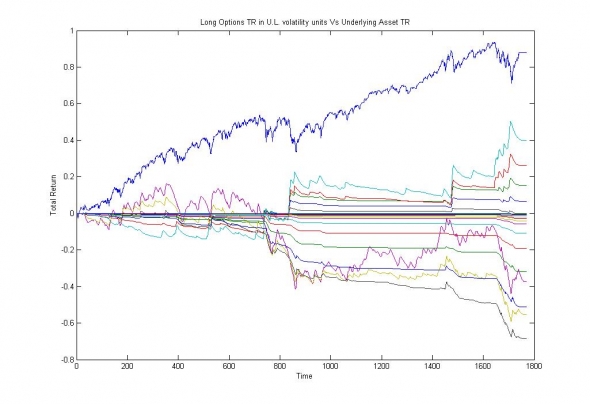
Изображение — Прибыль от удержания базового актива (синяя линия) и прибыль от удержания опционов различных страйков.



Для неискушенного взгляда всё просто прекрасно — стратегии по покупке опционов уверенно усредняются в ноль, индифферентно относятся к пертурбациям базового актива и не выходят, при этом, за рамки приличия, ограниченного геометрическим броуновским движением (GBM) для справедливых (STO) цен. Но, в действительности, это не более чем overfitting или, другими словами, недообучение модели.

Посмотрим теперь на этот результат через призму внутренней оценки модели, т.е. предполагаемого распределения цен базового актива на экспирацию:



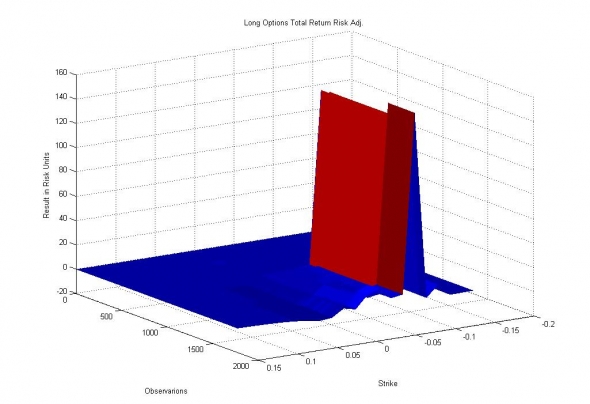
Изображение — Прибыль по стратегиям покупки опционов в единицах собственных оценок модели. 




Хорошо видна ступенька, возникающая в прибыли по 12%-му страйку Put опционов (которая будет убытком продавца в рамках модели игры покупателя и продавца), свидетельствующая о том, что в некоторый период низкой волатильности мы оценили вероятность взятия 12% страйка близкой к нулю, продали дешевые опционы за дорого (в текущем моменте) и ...  удивительным образом, повторили незавидную судьбу Ильи Коровина, ставшую уже притчей во языцех, и повествующую о том, как инвестиционный портфель опционов может быть единовременно слизан длинным языком Дракона.  



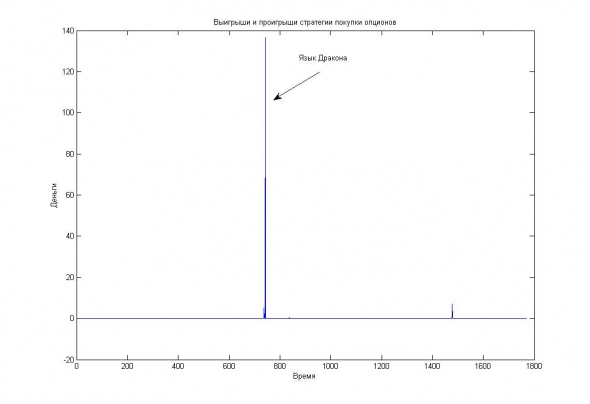
Изображение — Язык дракона на графике прибылей/убытков по покупке пут-опционов 12% страйка. 

 

По другим страйкам, надо отметить, ситуация не сильно лучше — результаты покупок лего отклоняются от нулевого равновесия на 10-20 среднеквадратичных отклонений (сигм).   


Теперь рассчитаем STO (smile theory optimal) цены опционов с учётом mean-reverse танца волатильности*: 

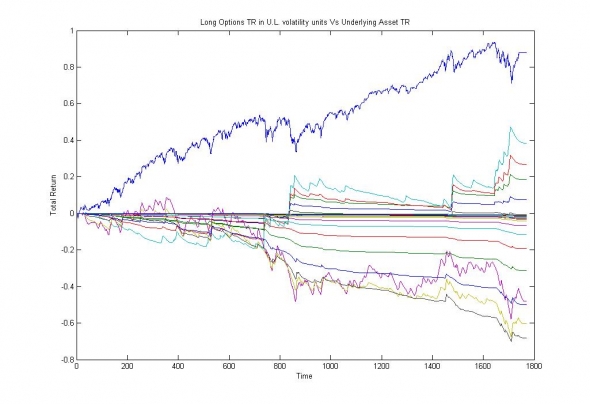
Изображение — Прибыль от удержания базового актива (синяя линия) и прибыль от удержания опционов различных страйков.



На первый взгляд  ничего не изменилось, кроме того, что мы покупали и продавали опционы совершенно по другим ценам и совершенно другим сценариям. Рассмотрим результаты стратегий через призму собственных оценок модели:



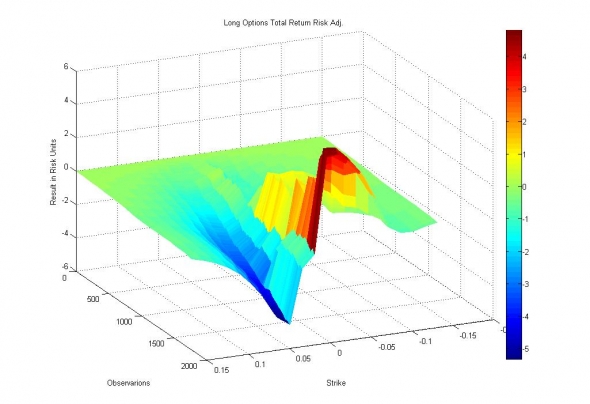
Изображение — Прибыль по стратегиям покупки опционов в единицах собственных оценок модели. 



Видно, что несмотря на то, что результаты несколько выходят за рамки приличия GBM и отклоняются от нуля вплоть до 5 сигма (из-за отсутствия put/call паритета), тем не менее,  в первом приближении, мы можем считать полученное ценообразование Nash-оптимальным, то есть не дающим преимущества ни покупателю, ни продавцу. Это стало результатом того, что при малой волатильности мы "покупали" опционы дорого, а при высокой — "продавали" опционы дешево. То есть в результате того, что мы совершали не совсем «рациональные» действия,  нам удалось избежать злой участи быть съеденным Драконом.

Вывод - без mean-reverse оценок волатильности сколько-нибудь адекватные модели опционного ценообразования не возможны. 


UPD:

Для полной чистоты эксперимента, приведем поверхность качества оценки опционов с учётом skew, но без mean-reverse :



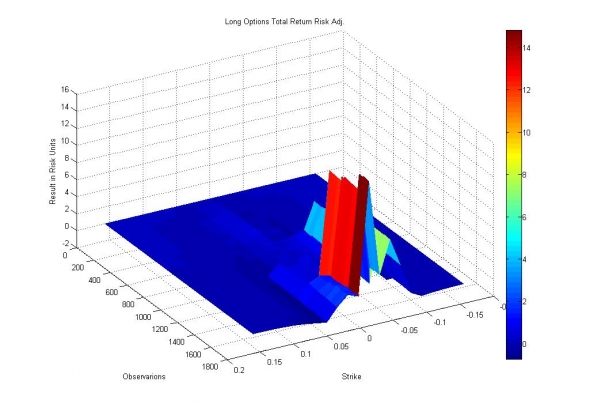
Изображение — Прибыль (накопленная) по стратегиям покупки опционов в единицах собственных оценок модели. 

Как видно — модель упорно совершает всю ту же ошибку — недооценивает опционы при низких значениях исторической волатильности.