Авторегрессия волатильности как задача для стохастического градиентного спуска.

Занимаясь первоначально исключительно портфельным инвестированием мы всё чаще сталкиваемся с задачей моделирования волатильности фондового рынка и его будущих ковариаций. Соответственно,  так или иначе, мы сталкиваемся с проблемой выбора модели, которая позволяла бы нам на самом широком диапазоне данных получать сколько-нибудь значимые оценки. 


В качестве показателя качества моделей нами была выбрана доля объяснённой дисперсии:





и промоделирована ошибка измерения волатильности заданного стационарного процесса на интересующем нас интервале: 



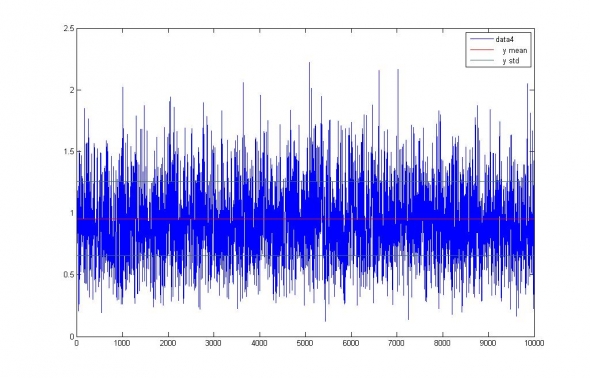
Рис.1. Измерение волатильности белого шума ~ N(0,1) на 5-и дневном интервале.

Среднеквадратичная ошибка измерения волатильности составила 0.3 = 30% от собственной волатильности шума. А прогностическая модель IV=1, то есть лучшая из всех возможных моделей, пользующаяся априорно известными данными, показала уровень качества  0.9.  Таким образом, мы получили оценку максимально возможной точности прогноза волатильности на период недельного интервала.


Для тестирования спектра моделей были выбраны акции ПАО Газпром и ПАО Сбербанк историей за 10 лет (Is выборка), в предположении покупки недельных опционов (5 дневная «OoS» выборка), по известной годовой предыстории (240 дневная выборка).


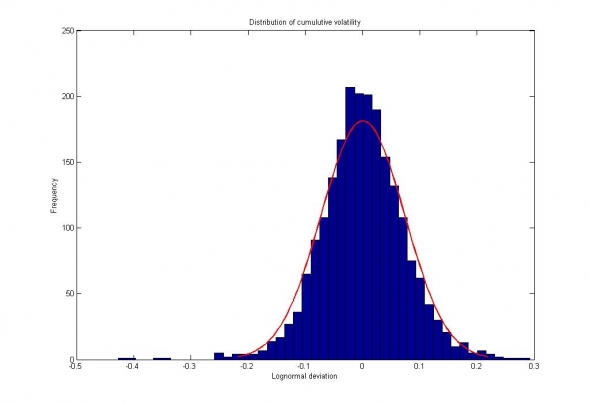
Рис. 2. Сбербанк. Распределение приращений цен за недельный интервал, представленное слабовыраженным распределением с «тяжелыми хвостами».



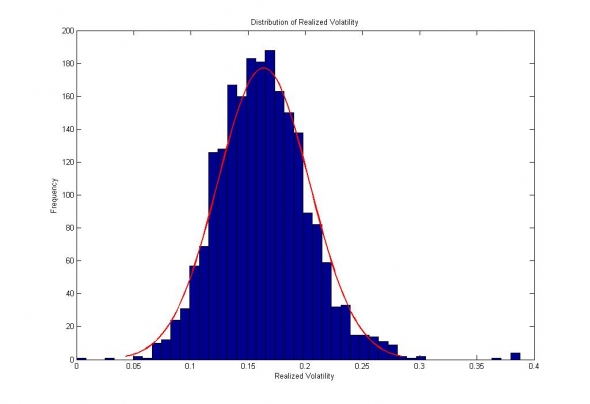
Рис.3. Сбербанк. Распределение измеренной волатильности внутри недельных интервалов.


В качестве авторегрессионных моделей волатильности мы взяли :

• Simple Moving Average 
• SVD-SSA 
• GARCH(1,0)    

                   

• ARCH(240)

                

• +некоторые другие

Как ни странно, наилучшими результатами отличились стандартные ARCH и GARCH модели :


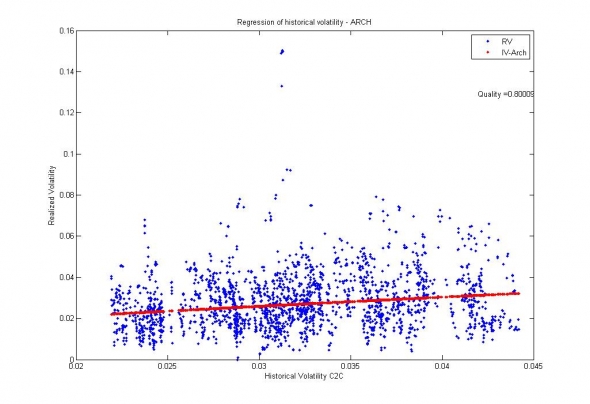
Рис. 4. Сбербанк. Обобщение данных GARCH(1,0) моделью. Доля объяснённой дисперсии = 0.8.


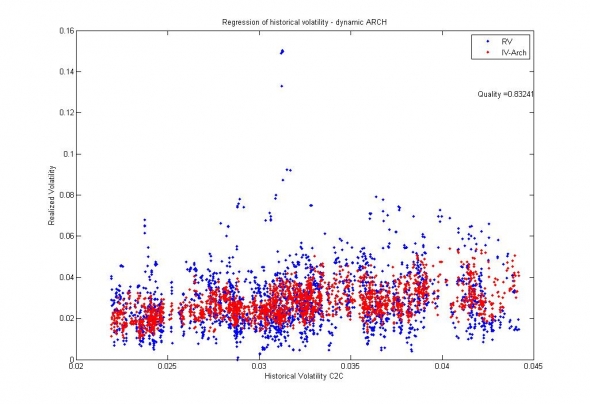
Рис. 5. Сбербанк. Обобщение данных АRCH(0,240) моделью. Доля объясненной дисперсии = 0.83;


Соответственно, с учётом предельной точности моделей 0.9, можно говорить о том, что ARCH и GARCH модели волатильности по отношению к рынку являются исчерпывающими, а их коэффициенты — стационарными, достаточными для того, чтобы можно было строить глобальные статистические модели, методом стохастического градиентного спуска.