12 ноября 2013, 12:19
Цена опциона. Часть 2. Улыбки, дельты, IV и RV.
Мысли навеяны обсуждениями в блогах:
http://smart-lab.ru/blog/150179.php про липкую дельту, сдвиг улыбки, и про то, что волатильности не существует.
http://smart-lab.ru/blog/150083.php упоминание Гнома про RV
http://smart-lab.ru/blog/149269.php мой последний блог «Цена опциона и Как правильно посчитать дельту?»
Мои рассуждения по теме.
Чтобы рассуждать про волатильность опциона, дельту, сдвиги улыбки нужно для начала дать этому всему определения. Сразу скажу, что книги по опционам на русском я читал по горизонтали, не вникал во все, что там написано, искал только интересующие меня вещи. Основную информацию я получал с сайтов университетов Европы и Америки, с сайтов забугровых квантов на нерусских языках. Я, конечно, не все понял, и не все из того, что понял, смогу доступно объяснить на русском, но я попробую.
Начинать нужно с цены опциона.
Цена — это денежное выражение стоимости товара.
Цена – это стоимость замещения.
Цена опциона должна быть равна затратам на хеджирование (дельта), плюс премия за риск.
Затраты на дельта-хеджирование будут зависеть от RV. RV полностью зависит от того как вы считаете дельту, и как хеджируетесь фьючерсом.
Считаю цену опциона любым методом. (Моя модель включает в себя одну единственную волатильность). Получились цифры, которые нужно как-то сравнивать с рынком. Самый простой способ сравнивать в волатильностях (ну так говорят, я спорить не буду, хотя можно и в пунктах). Биржа считает волатильности цен опционов по стаканам по BS. Я свои цены тоже переведу в волатильности по BS.
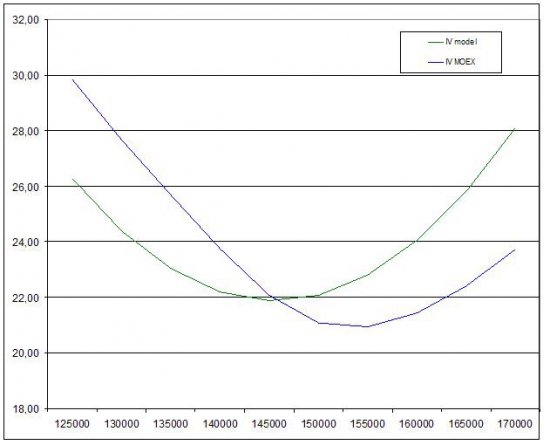
*Это цены с учетом затрат на хеджирование.
Я получил почти биржевую улыбку. Почти, потому что я не учел SKEW (уклон). Как я понимаю, этот уклон появляется в сторону наибольшего риска. На нашем рынке в текущий момент skew растет влево, т.е. риски растут при падении. Риски меряем в волатильности.
Добавляю в свою модель skew.
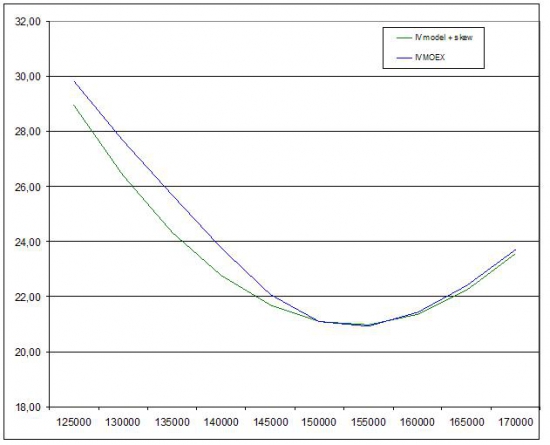
Вижу, что волатильности почти совпадают. Перекос в Путах считаю завышением цены в результате спроса. (хотя перекос может быть из-за другой skew)
Вывод: волатильностью по BS проще сравнивать цены, а в Вашей модели определения цены опциона ее может и не быть.
Теперь дальше. Есть цена опциона. Она почти совпадает с рынком, значит она справедлива в текущих условиях.
Дельта. Как ее считать? Если по BS, то при какой волатильности? IV? А какое отношение текущая IV рынка имеет к тому, как мы должны определять дельту?
Главный момент, для чего нам дельта – это для дельта-хеджирования. А дельта-хеджируем мы исходя их своих правил, т.е. сделки совершаем по RV.
Вывод: Дельту мы должны считать из своей IRV (Implied Realized Volatility).
Ну и последнее, про липкую дельту и возможное изменение волатильности, которое хочется учесть и захеджировать фьючерсом.
Опцион должен стоить столько, сколько волатильности реализуется за период (IRV), плюс премия за риск (это и будет моя справедливая цена). Если я продал опцион и хеджирую фьючерсом дельту (свою) и делаю это правильно, то я получу на выходе премию за риск, а если RV будет ниже, то и еще что-то останется.
А что будет, если я при расчете дельты буду учитывать возможное изменение волатильности?
Я уже продал опцион (допустим PUT). Все что мне нужно делать, чтобы получить премию за риск — это не потерять лишнее. Если я буду учитывать изменение волатильности то, как это делать правильно и улучшит ли это мой результат в долгосрочной перспективе?
Допустим, я учитываю тот факт, что вола растет при падении и сразу закладываю в модель, что вола падает при росте. А это правильно?
Мой ответ – нет. RV растет и при росте, и при падении. И если корректировать дельту по веге с учетом функции волатильности (skew), то вы скорректируете ее хорошо по отношению к IV, которая растет при падении, и падает при росте. Но для RV, от которой зависит ваша прибыль/убыток – затраты на хеджирование это будет скорее всего плохо.
Если при проданном опционе PUT, IV растет и приносит убыток продавцу, растет и дельта по BS. Если хеджировать эту дельту, а цена не упадет, а вырастет, то будет больший убыток по фьючерсу. То же самое будет, если прогнозировать рост IRV.
(за исключением некоторых моментов, когда сначала растет IV, а потом фьючерс сильно падает).
Вывод – «хорошо» захеджировать риск изменения волатильности фьючерсом невозможно, т.к. невозможно предсказать направление движения цены.
Тесты показывают, что в долгосрочной перспективе нет разницы, какую дельты использовать для хеджирования, IV или IRV. Хотя мой метод расчета IRV оставляет желать лучшего.
Я думаю, что риски по волатильности лучше хеджировать опционами. Главный вопрос как это правильно делать. А дельту нужно оставить в покое.
*Все рассуждения и выводы не являются окончательным мнением автора. Я просто в поиске новой информации, чтобы разложить все по полочкам.
*Выводы относительно дельта-хеджирования и корректировки дельты с учетом изменения волатильности (улыбки) относятся только к варианту с одним опционом в портфеле.
*Вопрос поднятый мной про правильную дельту в блоге http://smart-lab.ru/blog/149269.php остается для меня открытым. Буду рассматривать варианты с IRV. Если кто что подскажет буду благодарен. (я там вообще не учитывал изменение волы!!!)
*Спасибо Гному за термин RV. Я про него забыл и называл все это HV, а считал по своему.
http://smart-lab.ru/blog/150179.php про липкую дельту, сдвиг улыбки, и про то, что волатильности не существует.
http://smart-lab.ru/blog/150083.php упоминание Гнома про RV
http://smart-lab.ru/blog/149269.php мой последний блог «Цена опциона и Как правильно посчитать дельту?»
Мои рассуждения по теме.
Чтобы рассуждать про волатильность опциона, дельту, сдвиги улыбки нужно для начала дать этому всему определения. Сразу скажу, что книги по опционам на русском я читал по горизонтали, не вникал во все, что там написано, искал только интересующие меня вещи. Основную информацию я получал с сайтов университетов Европы и Америки, с сайтов забугровых квантов на нерусских языках. Я, конечно, не все понял, и не все из того, что понял, смогу доступно объяснить на русском, но я попробую.
Начинать нужно с цены опциона.
Цена — это денежное выражение стоимости товара.
Цена – это стоимость замещения.
Цена опциона должна быть равна затратам на хеджирование (дельта), плюс премия за риск.
Затраты на дельта-хеджирование будут зависеть от RV. RV полностью зависит от того как вы считаете дельту, и как хеджируетесь фьючерсом.
Считаю цену опциона любым методом. (Моя модель включает в себя одну единственную волатильность). Получились цифры, которые нужно как-то сравнивать с рынком. Самый простой способ сравнивать в волатильностях (ну так говорят, я спорить не буду, хотя можно и в пунктах). Биржа считает волатильности цен опционов по стаканам по BS. Я свои цены тоже переведу в волатильности по BS.
*Это цены с учетом затрат на хеджирование.
Я получил почти биржевую улыбку. Почти, потому что я не учел SKEW (уклон). Как я понимаю, этот уклон появляется в сторону наибольшего риска. На нашем рынке в текущий момент skew растет влево, т.е. риски растут при падении. Риски меряем в волатильности.
Добавляю в свою модель skew.
Вижу, что волатильности почти совпадают. Перекос в Путах считаю завышением цены в результате спроса. (хотя перекос может быть из-за другой skew)
Вывод: волатильностью по BS проще сравнивать цены, а в Вашей модели определения цены опциона ее может и не быть.
Теперь дальше. Есть цена опциона. Она почти совпадает с рынком, значит она справедлива в текущих условиях.
Дельта. Как ее считать? Если по BS, то при какой волатильности? IV? А какое отношение текущая IV рынка имеет к тому, как мы должны определять дельту?
Главный момент, для чего нам дельта – это для дельта-хеджирования. А дельта-хеджируем мы исходя их своих правил, т.е. сделки совершаем по RV.
Вывод: Дельту мы должны считать из своей IRV (Implied Realized Volatility).
Ну и последнее, про липкую дельту и возможное изменение волатильности, которое хочется учесть и захеджировать фьючерсом.
Опцион должен стоить столько, сколько волатильности реализуется за период (IRV), плюс премия за риск (это и будет моя справедливая цена). Если я продал опцион и хеджирую фьючерсом дельту (свою) и делаю это правильно, то я получу на выходе премию за риск, а если RV будет ниже, то и еще что-то останется.
А что будет, если я при расчете дельты буду учитывать возможное изменение волатильности?
Я уже продал опцион (допустим PUT). Все что мне нужно делать, чтобы получить премию за риск — это не потерять лишнее. Если я буду учитывать изменение волатильности то, как это делать правильно и улучшит ли это мой результат в долгосрочной перспективе?
Допустим, я учитываю тот факт, что вола растет при падении и сразу закладываю в модель, что вола падает при росте. А это правильно?
Мой ответ – нет. RV растет и при росте, и при падении. И если корректировать дельту по веге с учетом функции волатильности (skew), то вы скорректируете ее хорошо по отношению к IV, которая растет при падении, и падает при росте. Но для RV, от которой зависит ваша прибыль/убыток – затраты на хеджирование это будет скорее всего плохо.
Если при проданном опционе PUT, IV растет и приносит убыток продавцу, растет и дельта по BS. Если хеджировать эту дельту, а цена не упадет, а вырастет, то будет больший убыток по фьючерсу. То же самое будет, если прогнозировать рост IRV.
(за исключением некоторых моментов, когда сначала растет IV, а потом фьючерс сильно падает).
Вывод – «хорошо» захеджировать риск изменения волатильности фьючерсом невозможно, т.к. невозможно предсказать направление движения цены.
Тесты показывают, что в долгосрочной перспективе нет разницы, какую дельты использовать для хеджирования, IV или IRV. Хотя мой метод расчета IRV оставляет желать лучшего.
Я думаю, что риски по волатильности лучше хеджировать опционами. Главный вопрос как это правильно делать. А дельту нужно оставить в покое.
*Все рассуждения и выводы не являются окончательным мнением автора. Я просто в поиске новой информации, чтобы разложить все по полочкам.
*Выводы относительно дельта-хеджирования и корректировки дельты с учетом изменения волатильности (улыбки) относятся только к варианту с одним опционом в портфеле.
*Вопрос поднятый мной про правильную дельту в блоге http://smart-lab.ru/blog/149269.php остается для меня открытым. Буду рассматривать варианты с IRV. Если кто что подскажет буду благодарен. (я там вообще не учитывал изменение волы!!!)
*Спасибо Гному за термин RV. Я про него забыл и называл все это HV, а считал по своему.
Ставка и див отсечка лукойла уронят рынок ниже 2400
ГОЛОВА И ПЛЕЧИ КРАСНЫЙ НОС это ДЕДМОРОЗ
Я помню как меня обливали тут ну теперь
Правда очевидна что было что стало
Я понимаю кто это делал очень сильно РАСПСИХОВАНЫ и сидят ВУБЫТКЕ
2 536 776 575,00 Объем торгов
все просто и понятно особенно Москва сити в соседний кабинет зашел отдал рубли получил БИДКОИН
25% по ставке
Правильно говоришь 5000 цена будет на НН через 6 месяцев ну т.е 50 это цена после сплита кто не знал
Тонет, а сегодня и 20 ещё ниже уйдет. Вопрос в том, когда перейдем к росту?
Чёрный Доктор, совершенно верно, даже максимальный процентный доход сожгли, а у ранее размещенных депозитов еще и до 10% их тела.
Эдуард, ну, значит, покупаем Роснефть… это win-win
На «Казаньоргсинтезе» увеличили мощность производства ПВП на 120 тысяч тонн.
16.12.2024
«Казаньоргсинтез» (КОС, входит в «Сибур») завершил модернизацию одной из трех линий по производству полиэ...
AlexeyT
А. Г.
Стас Бржозовский
Андрей Агапов
karapuz
Гусев Михаил(debtUM)
Гном
dijap
FZF
Simix
dvoris
Дельта-хеджирование проданного опциона пут по IV опциона.
Дельта-хеджирование проданного опциона пут по RV.
Результат «немного» лучше.
Что мне не очень понравилось? Прежде всего, то, что skew, введенный в улыбку, как-то оказался просто skew. То есть, как бы он не имеет отношения к волатильности, а связан с некоторым столь же абстрактным «риском». Хотя по большому счету, цены на путы выше просто за счет (в среднем) роста волатильности при падении. Соответственно, если опцион выходит в область, где у него большая гамма (то есть, в деньги), то это одновременно означает, что волатильность выросла, и цена дельта-хеджа именно в той области, где он существенен, высока.
Понятие «рыночная цена риска» мне кстати, вообще не нравится. Поскольку оно введено исключительно для объяснения, почему опционы стоят дороже матожидания хеджа. Ну, ответ такой же, как почему полис ОСАГО стоит дороже, чем матожидание выплат — потому что страховые компании хотят платить сотрудникам и иметь прибыль. По поводу российского рынка, кстати, у меня нет уверенности, что в биржевых ценах есть эта самая премия за риск. Помнится, год назад на НОК-е мы сошлись на эту тему с Кулешевым (http://www.ilearney.com/info/news/ilearney_site/12335/?sphrase_id=19338). По его расчетам получалось, что премия есть, а по моим — что нет. Впрочем, периоды расчетов были разные. При этом крупняк OTC своим клиентам может давать вообще другие цены, причем в них, я уверен, в премией за риск все в порядке :).
-Возможно я неверно излагаю мысли. Что значит оказался просто skew? Можно назвать это функцией волатильности? Т.е. то, как меняется волатильность при движении вниз?
«путы выше просто за счет (в среднем) роста волатильности при падении»
— ну это и есть риск. Нет?
«Понятие «рыночная цена риска»
— про это не понял.
»потому что страховые компании хотят платить сотрудникам и иметь прибыль"
— стоимость затрат на хеджирование разная у разных участников. Если IV будет ниже RV, то я заработаю. Я хочу заработать больше, поэтому я стараюсь продать дороже, т.е. когда есть спрос и IV растет.
«у меня нет уверенности, что в биржевых ценах есть эта самая премия за риск.»
-это очень интересно, нужно подумать.
— по поводу skew — ну, я читаю то, что написано :). Поскольку то, как именно добавлен skew, не написано, то домысливаю, как могу. Может, здесь и не смог :).
— Рыночная цена риска и премия за риск более менее являются синонимами, как мне кажется. У Халла, насколько я помню, все же используется термин market price of risk.
— По поводу наличия премии у продавцов опционов — мне кажется, надо просто считать. Ну, кстати, совсем грубо это можно увидеть и примитивно наложив график индекса волатильности на график какой-нибудь HV (ну, месячной, например). Только RTSVX, наверное, нужно немного уменьшить (процентов на 5-6 у меня получалось в той презентации, что я выше упоминал). Ну, или уж дельта-хедж прогнать по всем правилам. Но это посложнее, да.
-нет, это проще :)
Да, для первого варианта, может действительно и есть смысл (вернее он точно есть) наиболее точно определять дельту (как липкую, как модифицированную липкую, еще как-то), потому как из-за нее и придется делать хеджирование, которое в итоге и приведет к какому-то результату, и недопонимание (ошибка) здесь может быть критичной.
Но для второго варианта (а я 90% в них), полагаю, что нет особой разницы, как мы считаем, это просто разные системы отсчета, кто-то живет по одной и хеджирует по своему (с определенной частотой, с оглядкой на дельту, гамму, другие греки), кто-то живет в другой системе отсчета, с другими правилами, а учитывая что в данном варианте, частое хеджирование губительнее, то может и нет особой разницы как редко! это делать. Для себя я вижу, что мне важнее потенциальная динамика греков (а не текущая статичная оценка, которая и так весьма абстрактна) по
1. абсолютной шкале X
2. относительной шкале X
3. с привнесением оценок вол (функций вол), пятью способами (обычно пользуюсь 2) в обоих пунктах выше
4. и отождествление оценок функций вол со статистическими.
И поигрывая этими графиками (греками), я вижу, что оценка греков не сильно то и отличается (отличается конечно, но все разумно), и разброс для меня вполне допустим.
Пока, для меня это работает, хотя может мега гэп по БА и/или воле, разорвет все шаблоны, тогда буду думать еще.
— по IV?
Поэтому, на мой взгляд, в частности, крайне опасно калибровать модели на отрезке, большая часть которого находится в зоне «аномалии». Либо по крайней мере нужно очень отчетливо признавать: мол, я ставлю на веру, что такая ситуация продлится еще сколько-то месяцев. Тогда, вероятно, действительно можно торговать по симметричной улыбке.
Биржевая от нее все еще сильно отличается, и при сохранении существующей ситуации, полагаю, это неплохой способ заработка. Пока ситуация не вернется к норме…
«Утверждение «RV растет и при росте, и при падении» также кажется мне, ну, скажем, не бесспорным. Наверное, на истории можно найти отдельные моменты «выносов» и «пробоев», но тем не менее в целом волатильность чаще всего растет при падении и чаще всего снижается при росте.»
Чаще всего… Т.е. это значит, что чаще всего будешь перестраховываться и недополучать, немного компенсировать когда это будет (падение цены и рост RV), а при росте фьюча и RV будешь сильно терять?
Если добавить к этому списку осень 2008-го, то частота таких событий, как падение рынка на 25-30%, в общем-то оказывается слишком высокой, чтобы ее игнорировать и ссылаться на единственного залетного черного лебедя…
А в такие моменты речь зачастую идет о чем-то большем, чем «перестраховаться и недополучить».
Я тоже предлагаю посмотреть на неё но с другого бока:
Цена опциона никогда не может быть высчитана рационально, т.к. она должна содержать в себе прогноз будущего. Пусть и в виде вероятности.
Поэтому опцион ничуть не лучше фьючерса в этом плане. А лучше фьюча он только тем, что имеет абсолютно рациональный параметр «тетта».
Итак, опцион для меня — это стоимость ожидания некоего движения к страйку IV.
А что мы можем этому противопоставить — это стратегия нашего ожидания этого события RV.
Если ты угадал стратегию движения — то профит, если не угадал — лось.
HV в данном случае это внешние условия, определяющие усилия продвижения по выбранной стратегии.
Знать её действительно необязательно, т.к. это величина случайная (функция от БА)
Есть волатильность, есть ожидаемая волатильность, есть волатильность волатильности…
-можно но не фьючерсом.
1. Термин «реализованная волатильность» — использовал «сколько себя помню опционщиком», т.к. он более точно отражает суть, чем «историческая волатильность».
2. Что такое IRV — мне не очень понятно (но обязуюсь вечером на свободную голову ещё раз всё перечитать). Чем она отличается от implied/«ожидаемой»/«подразумеваемой» волатильности? Всё это как раз некая мера ожидаемой болтанки цены БА, которую участники рынка закладывают в опционные премии.
3. Насчёт тестов. К бэктестам нужно относится аккуратно, т.к. история совсем небольшая, а опционы инструмент многомерный… в общем, бэктесты покрывают лишь небольшую долю пространства сценариев. Считаю, что лучше смотреть в сторону моделирования и управления рисками (сценарный подход).
4. Волатильность хеджирования (ВХ). Большая тема… :)
Общие принципы очевидны (всё для непрерывного хеджирования): а) ВХ = RV, «экватор», мы не зависим от направления движения БА — расходы на хедж фиксированы б) ВХ > RV, «недохедж», если БА пойдет направленно, то на гамма-отрицательных позициях будем получать больше убытка (хеджируем недостаточно, недополучаем доход от хеджа, недопокрываем убыток от опционов). Если останемся в «зоне комфорта» (в пределах гамма-фактора) — то заработаем больше, т.к. «распад и так идёт», а хеджировать надобности нет.
в) ВХ < RV, «перехедж», всё зеркально варианту б).
5. Насчёт того, что RV растет и при росте, и при падении. Почти верно. На самом деле вся динамика отражена в рыночных профилях IV и они давно уже достаточно «вылизаны». Рынок прайсит динамику реализованной волатильности за последние годы. Все явления, которые есть на улыбке, соответствуют явлениям которые были в RV: «ямка» справа (чем дальше по времени, тем правее), крылья, левое крыло выше (чем дальше по времени, тем выше). В общем, всё это есть в рыночной улыбке. Из-за эффекта «ямки», если смотреть корреляцию приращений цены и IV, то она будет отрицательная. Но динамика там богаче: если пойдем «резко вправо» то RV/IV тоже подрастет. Покажу картинкой:
Если в голове преобразуете цвет в «высоту улыбки», а ось Х нормируете на время, то узнаете привычный профиль рыночной улыбки.
да еще чтобы стало понятно, что это моя IV не для непрерывного хеджирования, а с учетом jump? Если у меня есть шаг хеджирования по дельте и цене? :)
— именно так я и торгую в реальности — сценарный подход. А бэктестами проверяю некоторые мысли и сценарии.
— суть вопроса не в мнении рынка, а в том, что дельта меняется по IV опциона, а фин.результат от дельта-хеджирования при реальной реализованной волатильности. IV опциона как бы показывает какая волатильность предположительно реализуется за период. Но реализуется она всегда по разному, сначала может быть высока, потом снизится, потом опять вырастет. Если я буду ориентироваться на IV, по при высокой RV, выше IV в моменте, или наоборот RV<IV в моменте, я буду, как-бы, неправильно хеджить дельту.
Тот способ по которому я считал RV, на длительных интервалах дает одинаковый с IV результат (по дельта хеджу), но в отдельные моменты значительно лучше по RV. Я ищу способ рассчитать IRV исходя из своего варианта дельта-хеджа. Возможно результат будет лучше. А пока торгую как и раньше.