05 января 2025, 14:07
Распределение вероятностей изменения цен, где Тяжелый Хвост?
Есть гипотеза что изменения цен на акции описываются гибридным распределением — нормальным для головы, и парето для хвоста.
Распределение парето f(x) = Cx^-a можно увидеть на лог/лог графике как прямую линию.
Я построил эмпирическое распределение CDF, реальных цен на акцию, но не могу найти на нем «хвост», прямую линию, где она? (просто для сравнения я также построил нормальное распределение откалиброванное на тех же данных).
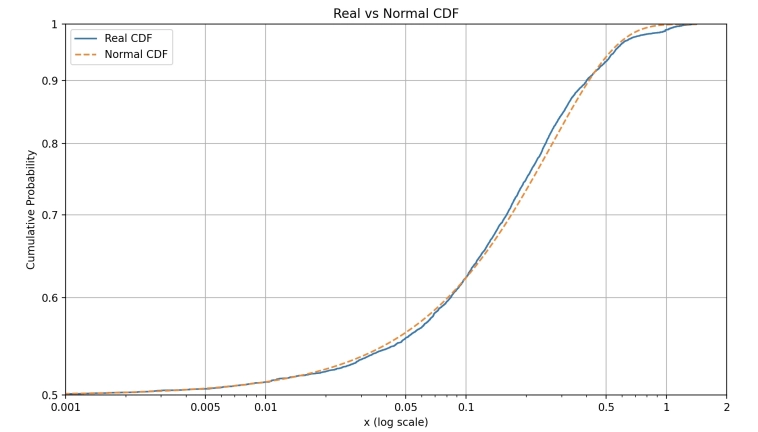
На графике показана только часть CDF, положительные измемения, в маштабле лог/лог. Также, изменения цен трансформированы, как: 1) лог траснформа и 2) отцентрированы относительно медианы. Нормальное распределение откалибровано на тех же трансформированных данных, с насильно принятым 0 взятым из медианы в качестве арифметического среднего (т.е. для нормального насильно поставлена медиана вместо арифметич среднего, так график лучше совпадает).
Данные — изменения цен на акцию, посчитаны как изменения за год, для каждого дня, diff_i=price_i/price_{i-360}, для цен одной акции за несколько десятилетий.
Вобщем, где на графике этот хвост? :)
АПДЕЙТ: Я неверно построил лог/лог график, нужно «перевернуть» график (комплементарную CDF построить, новый график снизу), тогда логарифмический масштаб гораздо лучше «растягивает» линию и она лучше видна (точнее то что никакой линии там нет). Видно что Нормальное Распределение недооценивает хвосты, и тяжелый хвост есть, но судя по всему не Парето, а что то послабее. Еще попробую варианты, и потом опубликую новые графики...

P.S.
В прошлых постах мне посоветовали посмотреть Обобщенное Гиперболическое Распределение (благодарность А. Г.). Я сомневался его использовать, поскольку там все таки не совсем Парето, но возможно оно реально хорошо подходит, попробую посмотрим...
Код и данные:
И данные скачать
Распределение парето f(x) = Cx^-a можно увидеть на лог/лог графике как прямую линию.
Я построил эмпирическое распределение CDF, реальных цен на акцию, но не могу найти на нем «хвост», прямую линию, где она? (просто для сравнения я также построил нормальное распределение откалиброванное на тех же данных).

На графике показана только часть CDF, положительные измемения, в маштабле лог/лог. Также, изменения цен трансформированы, как: 1) лог траснформа и 2) отцентрированы относительно медианы. Нормальное распределение откалибровано на тех же трансформированных данных, с насильно принятым 0 взятым из медианы в качестве арифметического среднего (т.е. для нормального насильно поставлена медиана вместо арифметич среднего, так график лучше совпадает).
Данные — изменения цен на акцию, посчитаны как изменения за год, для каждого дня, diff_i=price_i/price_{i-360}, для цен одной акции за несколько десятилетий.
Вобщем, где на графике этот хвост? :)
АПДЕЙТ: Я неверно построил лог/лог график, нужно «перевернуть» график (комплементарную CDF построить, новый график снизу), тогда логарифмический масштаб гораздо лучше «растягивает» линию и она лучше видна (точнее то что никакой линии там нет). Видно что Нормальное Распределение недооценивает хвосты, и тяжелый хвост есть, но судя по всему не Парето, а что то послабее. Еще попробую варианты, и потом опубликую новые графики...

P.S.
В прошлых постах мне посоветовали посмотреть Обобщенное Гиперболическое Распределение (благодарность А. Г.). Я сомневался его использовать, поскольку там все таки не совсем Парето, но возможно оно реально хорошо подходит, попробую посмотрим...
Код и данные:
import json
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# Loading 'diffs.json'
with open('diffs.json', 'r') as file:
diffs = json.load(file)
# Log-transform the data
log_diffs = np.log(diffs)
# Calculate the center as median, it fits better than the mean
center = np.median(log_diffs)
# Center the log diffs
log_diffs_centered = log_diffs - center
# Function to fit a real CDF
def fit_cdf_(data):
sorted_data = np.sort(data)
n = len(data)
cdf = [(x, (i + 1) / n) for i, x in enumerate(sorted_data)]
return cdf
# Fitting real CDF
real_cdf = fit_cdf_(log_diffs_centered)
# Fitting normal CDF, forcing mean to be 0
variance = np.mean(log_diffs_centered**2) # Variance
sigma = np.sqrt(variance) # Standard deviation
# Extract CDF x-values
cdf_xs = np.array([x for x, _ in real_cdf])
# Compute the normal CDF for these x-values
normal_cdf = [(x, norm.cdf(x, loc=0, scale=sigma)) for x in cdf_xs]
# Plot real CDF and normal CDF
real_cdf_ys = [p for _, p in real_cdf]
normal_cdf_ys = [p for _, p in normal_cdf]
plt.figure(figsize=(8, 6))
plt.plot(cdf_xs, real_cdf_ys, label='Real CDF', linestyle='-')
plt.plot(cdf_xs, normal_cdf_ys, label='Normal CDF', linestyle='--')
plt.xscale('log') # Logarithmic x-axis scale
plt.yscale('log') # Logarithmic x-axis scale
plt.ylim(0.5, 1) # y-axis domain
plt.xlim(0.001, 2) # x-axis domain
plt.xlabel('x (log scale)')
plt.ylabel('Cumulative Probability')
plt.title('Real vs Normal CDF')
plt.legend()
x_ticks = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 2]
plt.xticks(x_ticks, [str(label) for label in x_ticks])
y_ticks = [0.5, 0.6, 0.7, 0.8, 0.9, 1]
plt.yticks(y_ticks, [str(label) for label in y_ticks])
plt.grid(True)
plt.show()И данные скачать
Читайте на SMART-LAB:
⚙️ Лензолото: закат "пустышки"
Акции Лензолота резко упали. Что происходит — рассказывают аналитики Market Power Лензолото (LNZL) ➡️ Инфо и показатели Возможно, многие забыли, но еще в августе прошлого года...
18:55

📊 «МГКЛ»: выручка за январь 2026 года — 2,9 млрд руб.
Группа «МГКЛ» объявляет предварительные операционные результаты за январь 2026 года. По итогам первого месяца года: 📈 Выручка выросла в 4 раза по сравнению с январем 2025 года и...
10:00

Квазивалютный облигационный сегмент: что выбрать?
Погашение долларового выпуска «Газпрома» дает повод рассмотреть претендентов для валютного инвестирования в облигационном сегменте в перспективе одного года. 11 февраля 2026 года «Газпром...
18:46

Интер РАО. Неужели дивиденды будут минимальными за 3 года? Обзор производственных результатов и отчета РСБУ за Q4 2025г.
Вышел отчет по РСБУ за Q4 2025г. от компании Интер РАО: 👉Выручка — 15,49 млрд руб.(-14,0% г/г)
👉Себестоимость — 12,79 млрд руб.(-10,8% г/г)
👉Валовая прибыль — 2,70 млрд руб.(-26,7% г/г)...
15.02.2026










UPD. кстати, в фильме предел риска — как раз описана ситуация, когда хвосты вдруг стали толстеть
Самое интересное, что класс обобщенных гиперболических распределений — это класс распределений нормальных случайных величин со случайными средним и дисперсией и разными классами этих распределений. И в этом классе «лежит» почти все из распределений в справочниках по теорверу: и Хи-квадрат, и Лаплас и многое другое, кроме Парето.