| Число акций ао | 2 113 460 млн |
| Номинал ао | 0.5 руб |
| Тикер ао |
|
| Капит-я | 156,6 млрд |
| Выручка | 1 616,6 млрд |
| EBITDA | 612,6 млрд |
| Прибыль | -144,5 млрд |
| Дивиденд ао | – |
| P/E | -1,1 |
| P/S | 0,1 |
| P/BV | 0,1 |
| EV/EBITDA | 1,1 |
| Див.доход ао | 0,0% |
| Россети (ФСК) Календарь Акционеров | |
| Прошедшие события Добавить событие | |

Россети (ФСК) акции
0.07412₽ +1.31%
-






Друзья, кому-нибудь на сберброкер дивиденды пришли?
Артур,
нет мы как всегда после всех…
Любчик Александр, увы
Друзья, кому-нибудь на сберброкер дивиденды пришли?
Артур,
нет мы как всегда после всех…

Arti, вопрос такой: как полагаете, правильно ли сравнивать коэффициенты вариации цен акций разных компаний на предмет выводов о высокой/низкой волатильности и степени рисков? И, главное, почему?
Евдокимов Сергей, вопрос на самом деле очень интересный.
Базовый сценарий: У вас есть массив данных за какой-то период времени. Вы можете просто взять все эти цифры без привязки ко времени и построить гистограмму распределения цен. Можно посчитать выборочные среднее и дисперсию данной выборки, коэффициент вариации, интерквартильный размах и т.п. По этим метрикам можно сравнивать две разные выборки (акции двух разных компаний). Далее, можно провести проверку данного распределения на нормальность (или логнормальность) или принадлежность к другому классу распределений, и в случае, если проверка удачная, можно строить предположения даже о событиях, которые не встретились в выборке (допустим, об экстремально низких или экстремально высоких ценах).
Вопрос 1: Хотите ли вы учитывать фактор времени или нет? Почему это важно? Акция может двигаться, например, в рамках какого-то тренда, который достаточно предсказуем, а на этот тренд накладываются небольшие случайные колебания. Но если вы возьмете все это в одну корзину и отбросите фактор времени, то получится достаточно большой разброс (из-за тренда). Хотя между ценами в близкие дни разброс может быть совсем небольшой.
Таким образом, если не учитывать фактор времени, то акция, которая плавно растет от 100 до 200 в теч. всего года будет идентична по метрике коэффииента вариации акции, которая скачет каждый день от 100 до 200 и обратно. Важно ли для вас отличать эти два случая? В обоих этих случаях акции одинаково волатильны или же нет?
Вопрос 2: Хотите ли вы более корректно интерпретировать факт выплаты дивидендов? Падение цены на акцию может быть компенсировано выплатой дивидендов. Возможно, нужно будет сделать еще какие-то другие поправки.
Arti, начну со второго вопроса. Конечно правильно учитывать влияние выплаты дивидендов на волатильность акции. Но это на 2 порядка увеличивает трудоемкость работы, добавляет много ручного труда. Поэтому сей аспект пока опускаю и влияние дивидендов не учитываю.
Про фактор времени. Возможно, именно в этом и кроются мои сомнения. Возьму для примера пару акций. А дабы исключить офф-топ одна из них будет ФСК ))
Коэффициент вариации цены акции ФСК на интервале 2014-2019 с расчетом по среднеежедневным ценам (т.е. выборка данных максимальная, стандартное отклонение по генеральной совокупности) = 55%
И возьмем для сравнения Татнефть. У нее коэффициент = 79%
Согласно этим данным получается, что волатильность/риск у Татнефти выше. А так ли это в действительности ?
Акция ФСК за этот период выросла на 200%
А Татнефть — на 265%.
Т.е. тренд роста у Татнефти более восходящий, чем у ФСК. Вероятно именно этим и порождается бОльшее значение коэффициента вариации у Татнефти. Верно ?
Если верно, то тогда как правильно сравнить? Что надо сделать? Быть может пропорционально отклонению тренда пересчитать коэффициент? Или это будет некорректно?
На таком графике очевидно и понятно, чья волатильность выше и их можно сравнить. Обе цены вышли из одной точки в пришли в одну точку. Все просто.
А как сравнить акции с разными трендами ?

Евдокимов Сергей,
Можно попробовать «коэффициент колеблемости», аналог коэффициента вариации для трендов. В формуле коэффициента вместо среднеквадратичного отклонения от среднего использовать отклонение от трендовой линии.
LastChance, среднее значение — это конкретное число. Число на число я делить умею.
А тренд — это такая длинная прямая палкаколбасы. Как число поделить на палку?
Евдокимов Сергей,
Посмотрите формулу среднеквадратичного отклонения, там суммация отклонений для каждой точки от среднего: корень(сумм(yi-yср)/(n-1)). Так вот, надо подставить вместо среднего — значение на тренде в момент времени xi: корень(сумм(yi-yтрендi)/(n-2)). Еще раз yтрендi — значение на тренде в момент времени xi, свое для каждой точки.
LastChance, подскажите плиз, здесь точно должно быть минус 2, а не минус 1 ?

Евдокимов Сергей,
правильней n-2, так как здесь при оценке СКО добавляется еще одна степень свободы от линейной функции.
Arti, вопрос такой: как полагаете, правильно ли сравнивать коэффициенты вариации цен акций разных компаний на предмет выводов о высокой/низкой волатильности и степени рисков? И, главное, почему?
Евдокимов Сергей, вопрос на самом деле очень интересный.
Базовый сценарий: У вас есть массив данных за какой-то период времени. Вы можете просто взять все эти цифры без привязки ко времени и построить гистограмму распределения цен. Можно посчитать выборочные среднее и дисперсию данной выборки, коэффициент вариации, интерквартильный размах и т.п. По этим метрикам можно сравнивать две разные выборки (акции двух разных компаний). Далее, можно провести проверку данного распределения на нормальность (или логнормальность) или принадлежность к другому классу распределений, и в случае, если проверка удачная, можно строить предположения даже о событиях, которые не встретились в выборке (допустим, об экстремально низких или экстремально высоких ценах).
Вопрос 1: Хотите ли вы учитывать фактор времени или нет? Почему это важно? Акция может двигаться, например, в рамках какого-то тренда, который достаточно предсказуем, а на этот тренд накладываются небольшие случайные колебания. Но если вы возьмете все это в одну корзину и отбросите фактор времени, то получится достаточно большой разброс (из-за тренда). Хотя между ценами в близкие дни разброс может быть совсем небольшой.
Таким образом, если не учитывать фактор времени, то акция, которая плавно растет от 100 до 200 в теч. всего года будет идентична по метрике коэффииента вариации акции, которая скачет каждый день от 100 до 200 и обратно. Важно ли для вас отличать эти два случая? В обоих этих случаях акции одинаково волатильны или же нет?
Вопрос 2: Хотите ли вы более корректно интерпретировать факт выплаты дивидендов? Падение цены на акцию может быть компенсировано выплатой дивидендов. Возможно, нужно будет сделать еще какие-то другие поправки.
Arti, начну со второго вопроса. Конечно правильно учитывать влияние выплаты дивидендов на волатильность акции. Но это на 2 порядка увеличивает трудоемкость работы, добавляет много ручного труда. Поэтому сей аспект пока опускаю и влияние дивидендов не учитываю.
Про фактор времени. Возможно, именно в этом и кроются мои сомнения. Возьму для примера пару акций. А дабы исключить офф-топ одна из них будет ФСК ))
Коэффициент вариации цены акции ФСК на интервале 2014-2019 с расчетом по среднеежедневным ценам (т.е. выборка данных максимальная, стандартное отклонение по генеральной совокупности) = 55%
И возьмем для сравнения Татнефть. У нее коэффициент = 79%
Согласно этим данным получается, что волатильность/риск у Татнефти выше. А так ли это в действительности ?
Акция ФСК за этот период выросла на 200%
А Татнефть — на 265%.
Т.е. тренд роста у Татнефти более восходящий, чем у ФСК. Вероятно именно этим и порождается бОльшее значение коэффициента вариации у Татнефти. Верно ?
Если верно, то тогда как правильно сравнить? Что надо сделать? Быть может пропорционально отклонению тренда пересчитать коэффициент? Или это будет некорректно?
На таком графике очевидно и понятно, чья волатильность выше и их можно сравнить. Обе цены вышли из одной точки в пришли в одну точку. Все просто.
А как сравнить акции с разными трендами ?

Евдокимов Сергей,
Можно попробовать «коэффициент колеблемости», аналог коэффициента вариации для трендов. В формуле коэффициента вместо среднеквадратичного отклонения от среднего использовать отклонение от трендовой линии.
LastChance, среднее значение — это конкретное число. Число на число я делить умею.
А тренд — это такая длинная прямая палкаколбасы. Как число поделить на палку?
Евдокимов Сергей,
Посмотрите формулу среднеквадратичного отклонения, там суммация отклонений для каждой точки от среднего: корень(сумм(yi-yср)/(n-1)). Так вот, надо подставить вместо среднего — значение на тренде в момент времени xi: корень(сумм(yi-yтрендi)/(n-2)). Еще раз yтрендi — значение на тренде в момент времени xi, свое для каждой точки.
LastChance, подскажите плиз, здесь точно должно быть минус 2, а не минус 1 ?

 Наваял-таки фолмулку массива ))
Наваял-таки фолмулку массива ))
={ЕСЛИОШИБКА(КОРЕНЬ(СУММ(($B3:$G3-(НАКЛОН($B3:$G3;$B$2:$G$2)* $B$2:$G$2+ОТРЕЗОК($B3:$G3;$B$2:$G$2)))^2)/(СЧЁТ($B$2:$G$2)-1))/МНИМ.ABS(СРЗНАЧ($B3:$G3));"")}
Все четко считается. Кратенький отчет труда:
из электросетей самая низковолатильная выручка у МОЭСК, всего 1,5%. Практически лежит на тренде. Самая высокая у Северо-запада (=12,8%)
Наш ФСК имеет 9% ровно.
Самая же волатильная выручка из всех компаний у МКБ (=41%).
Следующая к расчетам — прибыль. Там, полагаю, качели будут пободрее )

LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами я тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
… Если риск — это исключительно волатильность, то как же быть с ценой, «точкой входа» относительно тренда. С точки зрения теории, циклические компании — все очень рискованные, но так ли это на самом деле.
Риторические вопросы. Разве не является менее рискованным зайти в нижней точке, купить ФСК по 0.04, ММК по 5 р (все модели покажут, что брать вообще не надо), чем по 40?
Где больший риск, покупка Татнефти по 800 в январе 2020 или по 400 в марте? По определению будет все просто: риск татнефти — высокий, высокая волатильность, скажем 50% вариация. Одинаков ли риск в разных точках?
Поэтому, с моей точки зрения всегда надо раскрывать, что такое риск (поэтому в первых постах я с этого и начал), а вообще лучше избегать этого слова, если под этим понимается другой термин (волатильность), то так и говорить.
Вопросы и мнение не для спора, тем более с докторами, чисто на интерес, на подумать, покрутить в голове, сам регулярно задумываюсь.
LastChance, почему же исключительно? Такого никто не утверждал, а даже наоборот.
Вы все верно указали: рисков много, всяких разных. И про использование терминологии с вами полностью согласен.
Указанные вами риски ичуть не менее опасны, нежели риск «волатильности цены акции» (так его обзову). Но прочие (важные с моей точки зрения) риски учитываю без расчетов и проблем нет. А риск волатильности надо считать, иначе никак. Посему и зятеял сию бадягу )
Евдокимов Сергей,
Можно уточнить, вы сами используете в принятии инвестиционных решений этот показатель (волатильность) или только участвуете в реализации методики?
Если используете, то как именно? Есть какие-то критические значения, при которых вы не будете брать? Или придаете какой-то весовой коэффициент в совокупности с другими показателями? Итоговое решение на основе комплекса показателей принимается субъективно или есть итоговая функция с критериями включения/исключения из портфеля?
LastChance,
1. Сам.
2. Сугубо веса по всем показателям. Именно здесь элемент субъективизма методики. Всё прочее только на жестких данных.
От ограничителей включения/выключения отказался. Ежели параметр важный и имеет сильно негативное значение, просто получает высокий вес и низкую оценку. Таким образом система автоматом отправляет бумагу в сад.
Евдокимов Сергей,
Ясно, спасибо за ответы.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами я тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
… Если риск — это исключительно волатильность, то как же быть с ценой, «точкой входа» относительно тренда. С точки зрения теории, циклические компании — все очень рискованные, но так ли это на самом деле.
Риторические вопросы. Разве не является менее рискованным зайти в нижней точке, купить ФСК по 0.04, ММК по 5 р (все модели покажут, что брать вообще не надо), чем по 40?
Где больший риск, покупка Татнефти по 800 в январе 2020 или по 400 в марте? По определению будет все просто: риск татнефти — высокий, высокая волатильность, скажем 50% вариация. Одинаков ли риск в разных точках?
Поэтому, с моей точки зрения всегда надо раскрывать, что такое риск (поэтому в первых постах я с этого и начал), а вообще лучше избегать этого слова, если под этим понимается другой термин (волатильность), то так и говорить.
Вопросы и мнение не для спора, тем более с докторами, чисто на интерес, на подумать, покрутить в голове, сам регулярно задумываюсь.
LastChance, почему же исключительно? Такого никто не утверждал, а даже наоборот.
Вы все верно указали: рисков много, всяких разных. И про использование терминологии с вами полностью согласен.
Указанные вами риски ичуть не менее опасны, нежели риск «волатильности цены акции» (так его обзову). Но прочие (важные с моей точки зрения) риски учитываю без расчетов и проблем нет. А риск волатильности надо считать, иначе никак. Посему и зятеял сию бадягу )
Евдокимов Сергей,
Можно уточнить, вы сами используете в принятии инвестиционных решений этот показатель (волатильность) или только участвуете в реализации методики?
Если используете, то как именно? Есть какие-то критические значения, при которых вы не будете брать? Или придаете какой-то весовой коэффициент в совокупности с другими показателями? Итоговое решение на основе комплекса показателей принимается субъективно или есть итоговая функция с критериями включения/исключения из портфеля?
LastChance,
1. Сам.
2. Сугубо веса по всем показателям. Именно здесь элемент субъективизма методики. Всё прочее только на жестких данных.
От ограничителей включения/выключения отказался. Ежели параметр важный и имеет сильно негативное значение, просто получает высокий вес и низкую оценку. Таким образом система автоматом отправляет бумагу в сад.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил… А про выручку и прибыль вполне верю, хороший подход на мой взгляд.
LastChance, признаюсь в этом месте (этим утверждением) вы меня немного удивили.
Как-бы получается вы верите в модель, которая описывает движение тела брошенного под углом к горизонту. Движение по параболе. И верите, что если брошенное яблоко полетит по параболе. Но почему-то не верите, что именно также полетит и брошенная груша. Странно ))
Евдокимов Сергей,
Поясню, немного запутал мб.
Волатильность можно и для цены считать и для выручки и для чего угодно.
Это я про риски другие имел ввиду, что график цены менее связан с рисками инвестирования в бизнес, чем графики выручки и прибыли. Цена может расти, а показатели выручки, прибыли уменьшаться, риски растут в моем понимании, хотя волатильности при этом может вообще не быть.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Про цену я не верил… А про выручку и прибыль вполне верю, хороший подход на мой взгляд.
LastChance, признаюсь, в этом месте (этим утверждением) вы меня немного удивили.
Как-бы получается вы верите в модель, которая описывает движение тела, брошенного под углом к горизонту. Движение по параболе. И верите, что брошенное яблоко полетит по параболе. Но почему-то не верите, что именно также полетит и брошенная груша. Странно ))
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами я тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
… Если риск — это исключительно волатильность, то как же быть с ценой, «точкой входа» относительно тренда. С точки зрения теории, циклические компании — все очень рискованные, но так ли это на самом деле.
Риторические вопросы. Разве не является менее рискованным зайти в нижней точке, купить ФСК по 0.04, ММК по 5 р (все модели покажут, что брать вообще не надо), чем по 40?
Где больший риск, покупка Татнефти по 800 в январе 2020 или по 400 в марте? По определению будет все просто: риск татнефти — высокий, высокая волатильность, скажем 50% вариация. Одинаков ли риск в разных точках?
Поэтому, с моей точки зрения всегда надо раскрывать, что такое риск (поэтому в первых постах я с этого и начал), а вообще лучше избегать этого слова, если под этим понимается другой термин (волатильность), то так и говорить.
Вопросы и мнение не для спора, тем более с докторами, чисто на интерес, на подумать, покрутить в голове, сам регулярно задумываюсь.
LastChance, почему же исключительно? Такого никто не утверждал, а даже наоборот.
Вы все верно указали: рисков много, всяких разных. И про использование терминологии с вами полностью согласен.
Указанные вами риски ичуть не менее опасны, нежели риск «волатильности цены акции» (так его обзову). Но прочие (важные с моей точки зрения) риски учитываю без расчетов и проблем нет. А риск волатильности надо считать, иначе никак. Посему и зятеял сию бадягу )
Евдокимов Сергей,
Можно уточнить, вы сами используете в принятии инвестиционных решений этот показатель (волатильность) или только участвуете в реализации методики?
Если используете, то как именно? Есть какие-то критические значения, при которых вы не будете брать? Или придаете какой-то весовой коэффициент в совокупности с другими показателями? Итоговое решение на основе комплекса показателей принимается субъективно или есть итоговая функция с критериями включения/исключения из портфеля?
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами я тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
… Если риск — это исключительно волатильность, то как же быть с ценой, «точкой входа» относительно тренда. С точки зрения теории, циклические компании — все очень рискованные, но так ли это на самом деле.
Риторические вопросы. Разве не является менее рискованным зайти в нижней точке, купить ФСК по 0.04, ММК по 5 р (все модели покажут, что брать вообще не надо), чем по 40?
Где больший риск, покупка Татнефти по 800 в январе 2020 или по 400 в марте? По определению будет все просто: риск татнефти — высокий, высокая волатильность, скажем 50% вариация. Одинаков ли риск в разных точках?
Поэтому, с моей точки зрения всегда надо раскрывать, что такое риск (поэтому в первых постах я с этого и начал), а вообще лучше избегать этого слова, если под этим понимается другой термин (волатильность), то так и говорить.
Вопросы и мнение не для спора, тем более с докторами, чисто на интерес, на подумать, покрутить в голове, сам регулярно задумываюсь.
LastChance, почему же исключительно? Такого никто не утверждал, а даже наоборот.
Вы все верно указали: рисков много, всяких разных. И про использование терминологии с вами полностью согласен.
Указанные вами риски ичуть не менее опасны, нежели риск «волатильности цены акции» (так его обзову). Но прочие (важные с моей точки зрения) риски учитываю без расчетов и проблем нет. А риск волатильности надо считать, иначе никак. Посему и зятеял сию бадягу )
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами я тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
Евдокимов Сергей,
Да все так, если чистую теорию использовать. Очень мне нравится философствовать на эту тему, потому как сам в поисках грааля и моя профессиональная деятельность непосредственно связана с оценкой рисков. А риск — очень философское понятие.
Если риск — это исключительно волатильность, то как же быть с ценой, «точкой входа» относительно тренда. С точки зрения теории, циклические компании — все очень рискованные, но так ли это на самом деле.
Риторические вопросы. Разве не является менее рискованным зайти в нижней точке, купить ФСК по 0.04, ММК по 5 р (все модели покажут, что брать вообще не надо), чем по 40?
Где больший риск, покупка Татнефти по 800 в январе 2020 или по 400 в марте? По определению будет все просто: риск татнефти — высокий, высокая волатильность, скажем 50% вариация. Одинаков ли риск в разных точках?
Поэтому, с моей точки зрения всегда надо раскрывать, что такое риск (поэтому в первых постах я с этого и начал), а вообще лучше избегать этого слова, если под этим понимается другой термин (волатильность), то так и говорить.
Вопросы и мнение не для спора, тем более с докторами, чисто на интерес, на подумать, покрутить в голове, сам регулярно задумываюсь.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
… Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.
LastChance, совершенно верно. Под риском в отношении цены акции/облигации я понимаю волатильность. Именно ее же под риском понимает и заслуженный экономист Российской федерации доктор экономических наук профессор НИУ Высшей Школы Экономики Берзон Николай Иосифович. О чем он и вещает в своих лекциях. Ни одной причины думать иначе, не верить, или подвергать сомнению его доводы у меня нет.
Иные риски, в том числе указанные вами, тоже безусловно учитываю. Считать их для этого вовсе не обязательно. Просто сравниваю/сопоставляю компании по каждому риску в отдельности и при прочих равных выбираю лучшие.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой скорректированной с вашей помощью методике точность значительно возрастёт.
Евдокимов Сергей,
Про цену я не верил, про что уже писал, почему. А про выручку и прибыль вполне верю, хороший подход на мой взгляд. Сам использую трендовую модель для выручки, но беру оттуда в анализ только процент годового роста.
Само применение термина «риск» меня вначале несколько смутило, но это нормально, потому что это понятие очень многогранное и каждый вкладывает в него свой смысл. Сейчас я уже проникся, что вы понимаете под этим волатильность показателя.
Для меня лично в волатильности нет никакого риска, так как я очень долгосрочный инвестор и мне не нужен стабильный денежный поток. Для меня здесь риск скорее в проблеме, если показатели прибыли/выручки упали и это нормально для этой компании (циклическая) восстановятся ли они на этот раз? Еще под рисками я понимаю покупку компании по дорогой цене, покупку компании с большой задолженностью (риск банкротства), риски, связанные с управлением. Однако эти риски очень сложно измерить и тем более сопоставить.

LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому ее среднее и равно
среднему значений тренда.
LastChance, ясно. Отлично. Спасибо.
А теперь скажите, почему в сию методологию вы не веруете? Скажу больше: с ее помощью я намерен вычислять и сравнивать стабильность получения выручки/прибыли*. Это же важно. Стабильность — признак мастерства. Если прибыль/выручка скачет от года к году как кузнечик на летнем лугу, то это более рискованное вложение инвестиций, нежели в компанию с четко и стабильно растущиими показателями.
* все это я уже давно сделал. Но по новой, скорректированной с вашей помощью методике, точность значительно возрастёт.
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее, можете пояснить/аргументировать?
Мне б сугубо для понимания )
Евдокимов Сергей,
Без разницы, средняя от цен акций равна средней значений на тренде. Вероятно, это можно показать зная, что трендовая линия (график линейной регрессии) получается с помощью метода наименьших квадратов, то есть при ее определении минимизируются квадраты отклонений точек от тренда. По сути получается некая «средняя линия» оптимальным образом описывающая исходное облако точек, поэтому среднее значений точек и равно среднему значений тренда.
Можете же легко посчитать и то и другое, в моем шаблоне получилось равенство. LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
LastChance, всё посчитал, все четко, все супер. Преогромное спасибо за «на водку» )
Если цены акции лежат на тренде, то расчетная дисперсия = 0, «псевдоНЕстандартное» отклонение = 0, коэффициент вариации = 0, волатильность = 0. Всё как и должно быть. Все как и хотел. Осталось все эти расчеты автоматизировать в макрокод (надеюсь получится) и провести сравнительный анализ рисков.
Последний вопрос: как полагаете, при расчете коэффициента вариации какое среднее значение правильнее использовать? Среднюю от цен акций? Или среднюю от значений на тренде? Вы это уже указывали, но для меня не очевидно, что так правильнее. Можете пояснить/аргументировать?
Мне б сугубо для понимания )
Arti, вопрос такой: как полагаете, правильно ли сравнивать коэффициенты вариации цен акций разных компаний на предмет выводов о высокой/низкой волатильности и степени рисков? И, главное, почему?
Евдокимов Сергей, вопрос на самом деле очень интересный.
Базовый сценарий: У вас есть массив данных за какой-то период времени. Вы можете просто взять все эти цифры без привязки ко времени и построить гистограмму распределения цен. Можно посчитать выборочные среднее и дисперсию данной выборки, коэффициент вариации, интерквартильный размах и т.п. По этим метрикам можно сравнивать две разные выборки (акции двух разных компаний). Далее, можно провести проверку данного распределения на нормальность (или логнормальность) или принадлежность к другому классу распределений, и в случае, если проверка удачная, можно строить предположения даже о событиях, которые не встретились в выборке (допустим, об экстремально низких или экстремально высоких ценах).
Вопрос 1: Хотите ли вы учитывать фактор времени или нет? Почему это важно? Акция может двигаться, например, в рамках какого-то тренда, который достаточно предсказуем, а на этот тренд накладываются небольшие случайные колебания. Но если вы возьмете все это в одну корзину и отбросите фактор времени, то получится достаточно большой разброс (из-за тренда). Хотя между ценами в близкие дни разброс может быть совсем небольшой.
Таким образом, если не учитывать фактор времени, то акция, которая плавно растет от 100 до 200 в теч. всего года будет идентична по метрике коэффииента вариации акции, которая скачет каждый день от 100 до 200 и обратно. Важно ли для вас отличать эти два случая? В обоих этих случаях акции одинаково волатильны или же нет?
Вопрос 2: Хотите ли вы более корректно интерпретировать факт выплаты дивидендов? Падение цены на акцию может быть компенсировано выплатой дивидендов. Возможно, нужно будет сделать еще какие-то другие поправки.
Arti, начну со второго вопроса. Конечно правильно учитывать влияние выплаты дивидендов на волатильность акции. Но это на 2 порядка увеличивает трудоемкость работы, добавляет много ручного труда. Поэтому сей аспект пока опускаю и влияние дивидендов не учитываю.
Про фактор времени. Возможно, именно в этом и кроются мои сомнения. Возьму для примера пару акций. А дабы исключить офф-топ одна из них будет ФСК ))
Коэффициент вариации цены акции ФСК на интервале 2014-2019 с расчетом по среднеежедневным ценам (т.е. выборка данных максимальная, стандартное отклонение по генеральной совокупности) = 55%
И возьмем для сравнения Татнефть. У нее коэффициент = 79%
Согласно этим данным получается, что волатильность/риск у Татнефти выше. А так ли это в действительности ?
Акция ФСК за этот период выросла на 200%
А Татнефть — на 265%.
Т.е. тренд роста у Татнефти более восходящий, чем у ФСК. Вероятно именно этим и порождается бОльшее значение коэффициента вариации у Татнефти. Верно ?
Если верно, то тогда как правильно сравнить? Что надо сделать? Быть может пропорционально отклонению тренда пересчитать коэффициент? Или это будет некорректно?
На таком графике очевидно и понятно, чья волатильность выше и их можно сравнить. Обе цены вышли из одной точки в пришли в одну точку. Все просто.
А как сравнить акции с разными трендами ?

Евдокимов Сергей,
Можно попробовать «коэффициент колеблемости», аналог коэффициента вариации для трендов. В формуле коэффициента вместо среднеквадратичного отклонения от среднего использовать отклонение от трендовой линии.
LastChance, среднее значение — это конкретное число. Число на число я делить умею.
А тренд — это такая длинная прямая палкаколбасы. Как число поделить на палку?
Евдокимов Сергей,
Посмотрите формулу среднеквадратичного отклонения, там суммация отклонений для каждой точки от среднего: корень(сумм(yi-yср)/(n-1)). Так вот, надо подставить вместо среднего — значение на тренде в момент времени xi: корень(сумм(yi-yтрендi)/(n-2)). Еще раз yтрендi — значение на тренде в момент времени xi, свое для каждой точки.
LastChance, ага, хорошо. Т.е. мне надо вычислить значение точки на тренде в каждой точке цены акций. Как, я пока еще не знаю. Наверное составить функцию тренда. Вообщем, есть над чем пораскинуть мозгами.
(формулы дисперсии, линейного, среднеквадратичного отклонения, коэффициентов вариации, осцилляции — знаю).
Допустим это псевдостандатное отклонение я как-то вычислю, но для сравнения волатильности разных акций мне нужны их коэффициенты вариации. Где делителем является среднее значение цен акции. Как с ним быть? Что вместо здесь вместо среднего воткнуть?
Евдокимов Сергей,
Да, по точкам провести тренд, получить параметры линии a,b. В экселе три варианта 1. можно построить диаграмму точечную с трендом и получить параметры 2. Можно воспользоваться функциями НАКЛОН и ОТРЕЗОК они дадут параметры тренда 3. Можно воспользоваться функцией ЛИНЕЙН, но она сложнее в понимании.
Подставляете все хi в полученную линейную функцию: yтрендi=axi+b
Подставляте yтрендi в формуле для СКО, которую я провел ранее.
Делите полученное СКО на обычное среднее (как и ранее при вычислении коэффициента вариации), чтобы получить «коэффициент колеблемости».
Вся фишка и получится, что вы используете отклонения не просто от среднего, а именно «расстояние» до трендовой линии.
LastChance, STOP!
Нашел ошибку. Все понял. Спасибо )
Вместо икса надо подставлять не цену акции, а месяц (он является аргументом), причем месяц в числовом значении, где, например, февраль 2020 года = 43862.
Arti, вопрос такой: как полагаете, правильно ли сравнивать коэффициенты вариации цен акций разных компаний на предмет выводов о высокой/низкой волатильности и степени рисков? И, главное, почему?
Евдокимов Сергей, вопрос на самом деле очень интересный.
Базовый сценарий: У вас есть массив данных за какой-то период времени. Вы можете просто взять все эти цифры без привязки ко времени и построить гистограмму распределения цен. Можно посчитать выборочные среднее и дисперсию данной выборки, коэффициент вариации, интерквартильный размах и т.п. По этим метрикам можно сравнивать две разные выборки (акции двух разных компаний). Далее, можно провести проверку данного распределения на нормальность (или логнормальность) или принадлежность к другому классу распределений, и в случае, если проверка удачная, можно строить предположения даже о событиях, которые не встретились в выборке (допустим, об экстремально низких или экстремально высоких ценах).
Вопрос 1: Хотите ли вы учитывать фактор времени или нет? Почему это важно? Акция может двигаться, например, в рамках какого-то тренда, который достаточно предсказуем, а на этот тренд накладываются небольшие случайные колебания. Но если вы возьмете все это в одну корзину и отбросите фактор времени, то получится достаточно большой разброс (из-за тренда). Хотя между ценами в близкие дни разброс может быть совсем небольшой.
Таким образом, если не учитывать фактор времени, то акция, которая плавно растет от 100 до 200 в теч. всего года будет идентична по метрике коэффииента вариации акции, которая скачет каждый день от 100 до 200 и обратно. Важно ли для вас отличать эти два случая? В обоих этих случаях акции одинаково волатильны или же нет?
Вопрос 2: Хотите ли вы более корректно интерпретировать факт выплаты дивидендов? Падение цены на акцию может быть компенсировано выплатой дивидендов. Возможно, нужно будет сделать еще какие-то другие поправки.
Arti, начну со второго вопроса. Конечно правильно учитывать влияние выплаты дивидендов на волатильность акции. Но это на 2 порядка увеличивает трудоемкость работы, добавляет много ручного труда. Поэтому сей аспект пока опускаю и влияние дивидендов не учитываю.
Про фактор времени. Возможно, именно в этом и кроются мои сомнения. Возьму для примера пару акций. А дабы исключить офф-топ одна из них будет ФСК ))
Коэффициент вариации цены акции ФСК на интервале 2014-2019 с расчетом по среднеежедневным ценам (т.е. выборка данных максимальная, стандартное отклонение по генеральной совокупности) = 55%
И возьмем для сравнения Татнефть. У нее коэффициент = 79%
Согласно этим данным получается, что волатильность/риск у Татнефти выше. А так ли это в действительности ?
Акция ФСК за этот период выросла на 200%
А Татнефть — на 265%.
Т.е. тренд роста у Татнефти более восходящий, чем у ФСК. Вероятно именно этим и порождается бОльшее значение коэффициента вариации у Татнефти. Верно ?
Если верно, то тогда как правильно сравнить? Что надо сделать? Быть может пропорционально отклонению тренда пересчитать коэффициент? Или это будет некорректно?
На таком графике очевидно и понятно, чья волатильность выше и их можно сравнить. Обе цены вышли из одной точки в пришли в одну точку. Все просто.
А как сравнить акции с разными трендами ?

Евдокимов Сергей,
Можно попробовать «коэффициент колеблемости», аналог коэффициента вариации для трендов. В формуле коэффициента вместо среднеквадратичного отклонения от среднего использовать отклонение от трендовой линии.
LastChance, среднее значение — это конкретное число. Число на число я делить умею.
А тренд — это такая длинная прямая палкаколбасы. Как число поделить на палку?
Евдокимов Сергей,
Посмотрите формулу среднеквадратичного отклонения, там суммация отклонений для каждой точки от среднего: корень(сумм(yi-yср)/(n-1)). Так вот, надо подставить вместо среднего — значение на тренде в момент времени xi: корень(сумм(yi-yтрендi)/(n-2)). Еще раз yтрендi — значение на тренде в момент времени xi, свое для каждой точки.
LastChance, ага, хорошо. Т.е. мне надо вычислить значение точки на тренде в каждой точке цены акций. Как, я пока еще не знаю. Наверное составить функцию тренда. Вообщем, есть над чем пораскинуть мозгами.
(формулы дисперсии, линейного, среднеквадратичного отклонения, коэффициентов вариации, осцилляции — знаю).
Допустим это псевдостандатное отклонение я как-то вычислю, но для сравнения волатильности разных акций мне нужны их коэффициенты вариации. Где делителем является среднее значение цен акции. Как с ним быть? Что вместо здесь вместо среднего воткнуть?
Евдокимов Сергей,
Да, по точкам провести тренд, получить параметры линии a,b. В экселе три варианта 1. можно построить диаграмму точечную с трендом и получить параметры 2. Можно воспользоваться функциями НАКЛОН и ОТРЕЗОК они дадут параметры тренда 3. Можно воспользоваться функцией ЛИНЕЙН, но она сложнее в понимании.
Подставляете все хi в полученную линейную функцию: yтрендi=axi+b
Подставляте yтрендi в формуле для СКО, которую я провел ранее.
Делите полученное СКО на обычное среднее (как и ранее при вычислении коэффициента вариации), чтобы получить «коэффициент колеблемости».
Вся фишка и получится, что вы используете отклонения не просто от среднего, а именно «расстояние» до трендовой линии.
LastChance, продвижение есть, но воткнулсо в преграду. Нужна помощь )
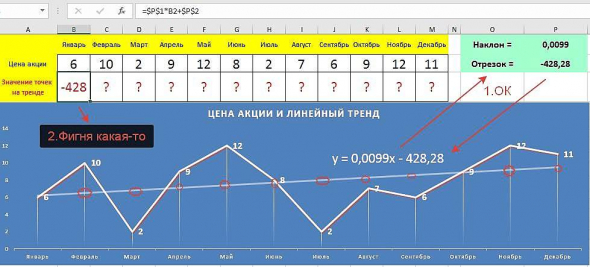
1. Итак, уравнение тренда построил. Двумя способами: и графически, и с помощью формул «наклон-отрезок». Все совпало, а значит ошибки нет.
2. Теперь мне надо найти значение точек на тренде в моменте цен акции. Использую полученное уравнение, подставляю вместо икса цену акции получаю «фигню какую-то» (см. на рисунке)
Подскажите плиз, что делаю неправильно ?

Сбер(брокер) придержит минимум 3 дня.
Уважаемый Burtlik,
С Газпромбанком всегда такая же фигня!!!
Россети (ФСК) - факторы роста и падения акций
- Россети-ФСК оценена ниже своих реальных чистых активов в 6,5 раз. и ниже НОМИНАЛА почти в 5 раз. При этом работает с прибылью. р.е = 2 (28.07.2023)
- правительству поручено "оптимизировать" инвестпрограмму в плане снижения ее финансирования в 2023-2027 гг. и переноса сроков некоторых проектов, рассмотреть вопрос о дальнейшей индексации тарифов (в мае был повышен тариф для ЕНЭС на 6,3% - ИФ). (18.08.2023)
- Чистая прибыль на акцию по РСБУ за 9м23г = 0,24057р. при рыночной стоимости 0,128р. (04.11.2023)
- Единственная АО имеющая рыночную стоимость в 4 раза ниже НОМИНАЛА = 50к.! при этом только доли дочерних компаний торгуемых в рынке оцениваются в 2 раза выше всей ФСК Россетей. так же у ФСК Россети 8,57% ИРАО. балансовая стоимость Чистых активов = 1,8 трл.р при рыночной капитализации 0,27трл.р. компания работает с хорошей прибылью, Чистые активы растут ежегодно (15.01.2024)
- Реальный свободный денежный поток компании гораздо меньше ее прибыли, по причине того, что существенная ее часть тратится на стройку. (15.07.2019)
- Новые построенные мощности не увеличивают выручку но увеличивают амортизацию и тем самым сокращают прибыль (24.10.2021)
- Прибыльность компании в 2021 году начала снижаться из-за того, что затраты растут опережающими выручку темпами (10.02.2022)
- Инвестпрограмма на 2023-2024г. превысит 1 трлн.руб. (29.12.2023)
- Из-за высокой ставки ЦБ в 2024г. резко вырастут процентные расходы (90% облигаций с плавающим купоном КС+премия) (29.12.2023)
- Дивидендов до 2026 года не ожидается - решение Президента РФ В. Путина (29.12.2023)
⚠️ Если вы считаете, что какой-то фактор роста/падения больше не является актуальным, выделите его и нажмите CTRL+ENTER на клавиатуре, чтобы сообщить нам.
Россети (ФСК) - описание компании
ФСК ЕЭС — крупнейшая в мире публичная электросетевая компания, является монопольным оператором Единой национальной электрической сети России. Компания управляет более 131 тыс. км линий электропередачи и обладает общей трансформаторной мощностью более 334,8 тыс. МВА. Крупнейшим акционером ФСК с долей 80,6 процентов является компания «Россети».ПАО «ФСК ЕЭС» планирует в 2015 года получить прибыль по РСБУ в объеме не менее 8 млрд рублей.
Годовой отчет ФСК ЕЭС 2015
Сайт ФСК ЕЭС: http://www.fsk-ees.ru/
 Финаме
Финаме БКС Мир Инвестиций
БКС Мир Инвестиций
















