О ценах, модели Блэка-Шоулза и графическом анализе. Часть 1

Эту таблицу я впервые приводил в своем выступлении на конференции Смартлаба  весной 2016-го и повторил на конференции 2018-го, акцентировав внимание на том, что хочу оформить письменно ниже

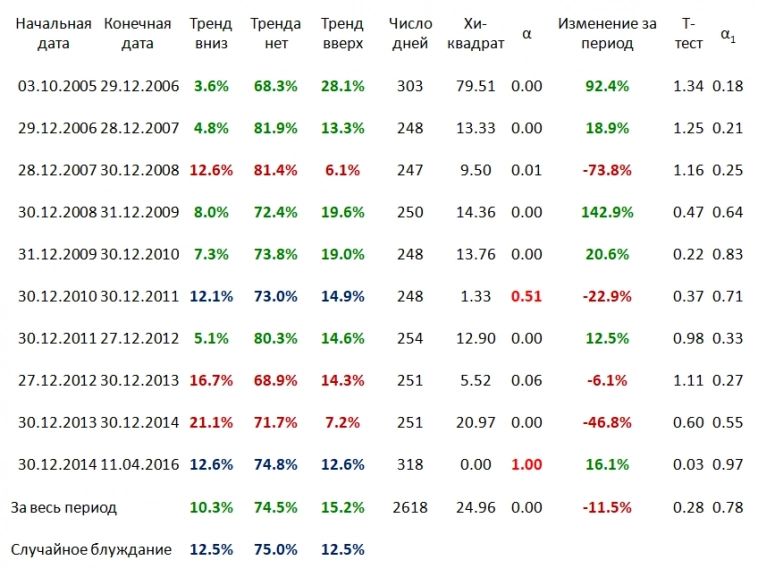
Что в таблице?  В таблице доли участков RI (фьючерс на индекс РТС — прим. мое) из 10 приращений, как по отдельным периодам, так и в целом, которые я отнес к «трендам». Что я считал «трендом»? «Трендом» я считал участки, на которых среднее приращений цен (или приращений логарифмов цен, что эквивалентно) отлично от нуля и если оно больше нуля, то относим отрезок к «трендам вверх», а если меньше нуля – к «трендам вниз».

 Какой использовался критерий? Обычный модифицированный критерий Стьюдента на отличие приращений логарифма(!) цены от приращений гауссовского процесса со средним нуль  и дисперсией «почти равной» для 9 испытаний из 10 (нулевая гипотеза). Так как мы имеем критерий на различие сложной гипотезы против простой, то распределение статистики критерия точно известно нам только  при простой гипотезе. И потому при априори выбранных границах критерия мы можем знать только вероятности попадания последовательности из 10 значений в наши «классы» при верности нулевой гипотезы.

Границы я выбрал так, что при нулевой гипотезе вероятность попадания в «тренды вверх» («тренды вниз») – 0,125. И нас будут интересовать отличия долей в реальных ценах от долей в нулевой гипотезе.

Что нам показывает столбец альфа из таблицы? Альфа – это вероятность того, что мы ошибемся, если отвергнем нулевую гипотезу. Как мы видим эта вероятность близка к нулю для 8 периодов из 10 и в целом для совокупности. НО! Если мы взглянем на столбец, где стоит альфа1, равная вероятности ошибки отвергнув гипотезу, что вероятность «трендов нет» 0,75=1-2*0.125, то увидим, что эта вероятность ошибки очень велика, как для отдельных периодов, так и для совокупности в целом.

Что это значит? А то, что с вероятностью больше 0,99 приращения логарифмов цен не могут быть приращениями  гауссовского процесса с постоянным(!) средним   и «медленно меняющейся» дисперсией для подавляющего большинства времени.

А что такое гауссовский процесс с постоянным(!) средним   и «медленно меняющейся» дисперсией для подавляющего большинства времени? Это модель Блэка-Шоулза и ее ARCH-GARCH обобщения. Получается, что эти модели не соответствуют рынку.

Наверное можно придумать  модель гауссовского  процесса с постоянным(!) средним   и дисперсией, «прыгающей как больная белочка», которой не противоречат полученные частоты, но самой простой моделью, объясняющей такое распределение частот является  модель гауссовского  процесса с переменным(!) средним .

Так, для справки, выборочное одномерное распределение   частот значений  гауссовского  процесса с переменным(!) средним будет близко к обобщенному гиперболическому распределению, а не к нормальному, т. е. иметь «тяжелые хвосты». Поэтому аргумент про «тяжелые хвосты» вовсе не опровергает гипотезу гауссовости процесса.

Заканчивая с анализом приведенной таблицы, отметим еще один интересный факт. На всем рассматриваемом отрезке  RI немного упал (правда, статистически это падение неотличимо от нуля), а доля «трендов вверх» больше доли «трендов вниз». Что это значит? Да известный факт: росты на фондовом рынке «положе»,  а падения «круче». И, кстати, в 8 из 10 периодов «работает» закономерность: если доля «трендов вверх» больше доли «трендов вниз», то RI вырос (зеленые строки) и наоборот (красные строки). Вроде логично, но есть и исключения — синие строки.

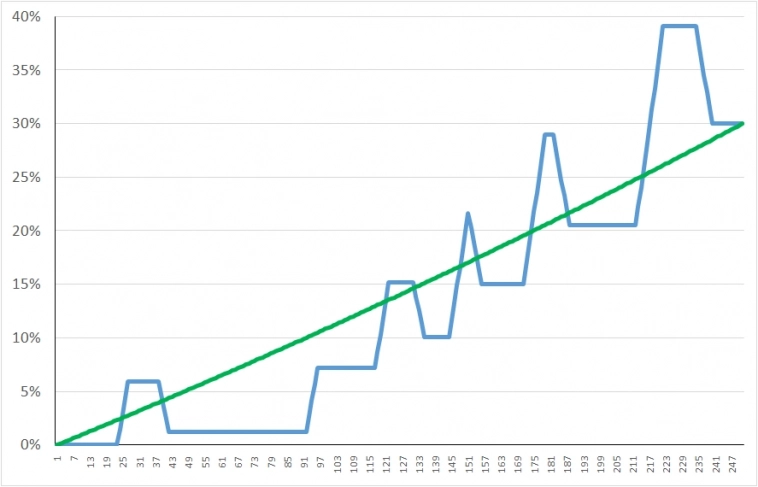
Добавим к переменности среднего еще и гипотезу кусочного постоянства. Как выглядит кривая среднего случайного блуждания, приращения которого являются  таким гауссовским процессом?

Это будет ломанная линия. Как эта голубая  линия, если сумма выросла

Или так, если сумма упала

Зеленая прямая на первом рисунке – это среднее случайного блуждания  с постоянным положительным средним.

Ну а траектории (реализации) нашего случайного блуждания будут кривыми, совершающими «относительно небольшие» колебания вокруг синей линии.  «Относительно небольшие» — это значит гораздо  меньше среднего размера растущих и падающих участков ломанной.

И вот тут мы подходим к самому интересному. На подобных траекториях «задним числом» легко рисуются такие фигуры из планиметрии, как треугольники (они же «вымпелы» или «бабочки»), параллепипеды (они же прямоугольники, «коридоры» или  «флаги»), ромбы (они же «бриллианты») и трапеции.  А если пренебречь погрешностью  в несколько процентов (для дневок) между реальными локальными экстремумами траектории и уровнями Фибоначчи, то можно построить и «разволновку по Эллиотту», причем с такими погрешностями и не одну.

НО! Если дополнительно предположить, что точки перелома ломанной абсолютно непредсказуемы, то «ценность» подобных рисований равна нулю.  Почему? Потому что предсказать точки перелома невозможно (см. предположение), а лучшим индикатором, выявляющим эти точки перелома постфактум, являются простейшие полосы Боллинджера, построенные по приращениям траектории (не значениям) с точки предыдущего перелома.

В отличии от гауссовости и кусочного постоянства средних  статистически доказать гипотезу абсолютной непредсказуемости точек перелома ломанной невозможно. Доказать непредсказуемость можно только для частных случаев прошлой информации или опровергнуть в целом. О ее доказательстве для частных случаев прошлой информации я напишу во второй части, а пока, предваряя ожидаемое возражение, сделаю одно важное замечание.

Предвижу возражение: «Какие логарифмы цен – мы работаем с ценами, а не с логарифмами!». Господа, вспомните курс средней школы: логарифм – абсолютно непрерывная монотонная функция на отрезке от 0 до бесконечности. Что это значит? А то, что все «ужимки и прыжки» свечного графика цен через взаимно однозначный пересчет «перекочуют» на график логарифмов и наоборот. А вместе с этим «перекочуют» и любые фигуры и паттерны, а также  «волны Эллиотта» просто с другими числовыми значениями. А значит то, что я сформулировал в рамках гипотезы абсолютной непредсказуемости, верно и для самих цен.