Случайное или не случайное

Математики заявляют, что котировки инструмента — это случайный процесс.

Многие не знакомые с этим понятием заявляют, что цена инструмента не может быть случайной, ведь покупают и продают люди, которые свои решения принимают на основании какой-то информации и эти решения не случайны. Помимо людей на бирже торгуют роботы, которые также как и люди свои решения принимают на основании какой-то информации, четко следуя заданному алгоритму и эти решения тоже не являются случайными.

Верно здесь и то и другое, просто люди (знакомые с понятием «случайный процесс» и не знакомые) говорят о разных аспектах одного и того же.

Безусловно торгующие люди и роботы принимают не случайные решения и действия, но совокупности таких решений и действий создают в результате такие движения цены, что становится невозможно точно (вот здесь именно точно, не примерно) предсказать цены инструмента наперед. Иногда такие совокупные решения (не случайные решения и действия людей и роботов) приводят к направленным движениями рынка, иногда приводят к боковику, но в целом когда мы рассматривает получаемый результат, то мы не можем точно (если хотите до копейки) предсказать какая цена будет на следующем баре, мы можем лишь «очертить» границы, представить «интервалы» в которых будет цена, а может и не будет. И вот такой процесс в котором невозможно предсказать точное (точное, до копейки) значение цены, а возможно лишь описать границы называется случайным. Случаен он не из-за того, что были приняты случайные решения, а из-за того, что совокупности, в нашем случае (в биржевой торговле) не случайных решений, приводят к тому, что становится невозможно точно до копейки предсказать какая цена будет в будущем (на следующем баре, через час, через день или как вам нужно), а можно лишь говорить о границах возможного. А описанные границы (не важно каким способом получены) не являются жестко заданными, это лишь о том, что скорее всего цена будет там, но все может быть по другому.

И так вернемся к случайным процессам и зайдем немного с другой стороны (надеюсь не сильно меня будут пинать матёрые математики за такой подход и допущенные упрощения)...

Например, мы можем задать уравнение прямой, которое будет описывать какой-то не случайный процесс, пусть это будет: y = 5.33*x

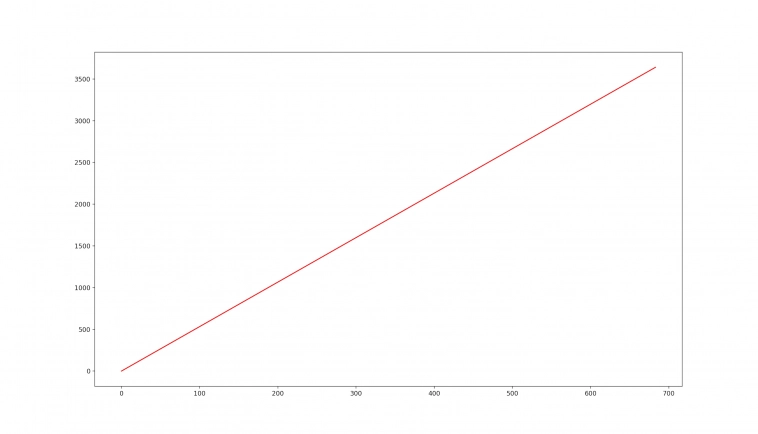
Т.е. для любого x мы можем абсолютно точно (точно «до копейки») вычислить y, предсказывать такой процесс мы можем на неограниченное будущее вперед (мы можем представить, что x — время, а y — это цена и цены при таком процессе мы можем предсказывать на любое количество «дней» вперед, причем сделать это можем с точностью до копейки).

А сейчас давайте введем какой-то случайный процесс (обозначим его буквой e), который будет с течением времени задавать какие-то колебания вокруг нуля, такой процесс мы опишем в виде уравнения y = e. Описать в явном виде мы его не можем, но представим, что это какие-то колебания «туда-сюда». Например, возьмем колебания как на изображении ниже.

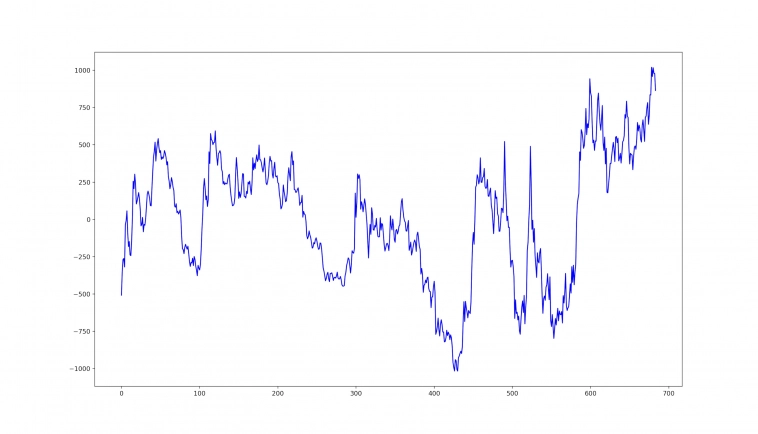
Далее в уравнение нашей прямой (нашего первоначального не случайного процесса) мы добавим эту случайную компоненту, т.е. теперь наше уравнение будет y = 5.33*x + e

Графически это будет выглядеть так:

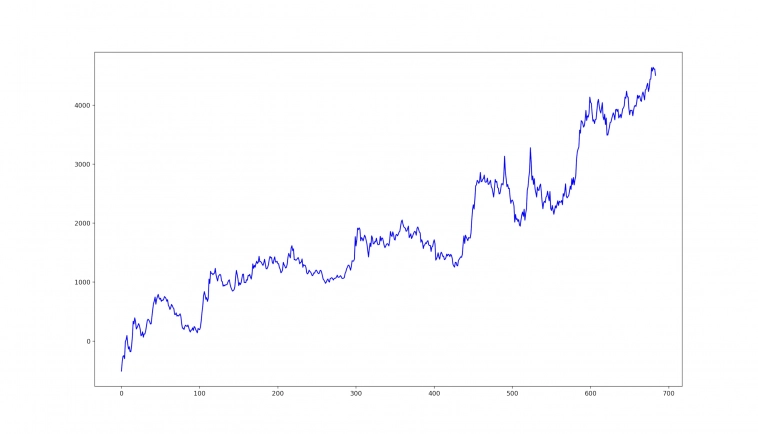
Здесь наблюдаем почти такой же процесс как исходный (идет в ту же сторону), но уже мы не можем точно предсказать какие будут «y» (игреки), мы можем лишь оценить границы в каких этот «y» (игрек) может быть, а «средняя» этого процесса осталась той же самой y = 5.33*x

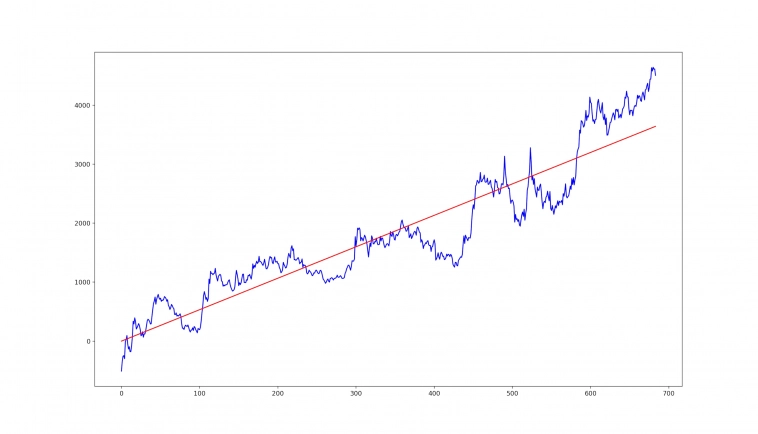
Этот полученный процесс (y = 5.33*x + e) уже является случайным процессом, т.е. другими словами случайный процесс может в своей основе содержать абсолютно не случайную основу, но в то же время иметь случайную компоненту (кто-то говорит о случайном блуждании, кто-то говорит о шумах, кто-то говорит о броуновском движении и т.д.), которая не позволяет предсказывать до «копейки» будущие значения наших y (цен). А случайная компонента нашего не случайного процесса может возникать, например, из-за того, что все сделки на бирже исполняются последовательно (одна за другой) в том порядке, в котором поступили они на обработку на биржу, а уже порядок поступления этих заявок случаен (разные люди/роботы в разное время принимают решения (кто-то думает дольше, кто-то быстрее), заявки на биржу поступают с непредсказуемыми задержками, «пакеты по сети» идут различными маршрутами) и из-за порядка выполнения возникают движения цены то вверх, то вниз (может быть несколько движений вверх, а потом вниз или еще как-то по другому)), затем отдельные сделки группируются в свечи/бары формируя тем самым какие-то направленные (или не направленные) движения.

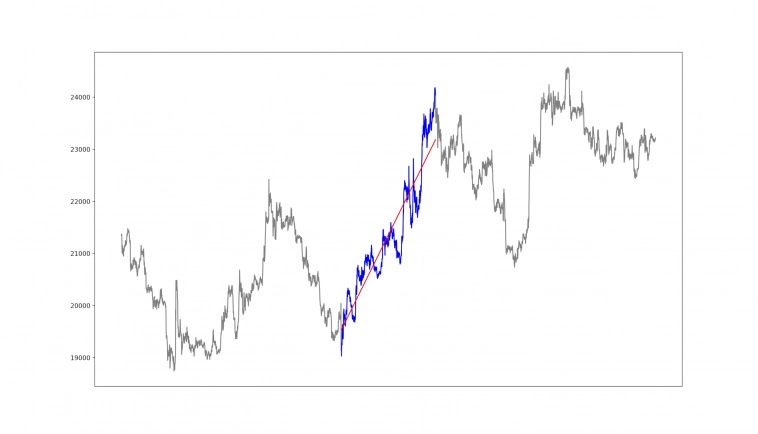
Предложенная выше модель (y = 5.33*x) в виде линейной зависимости y от x по сути может быть очень упрощенным приближением какого-то отрезка движения цены инструмента (см. рисунок выше), фактически может описывать направление движения цены, «усредняя» движения цены вверх/вниз. Такую модель (называется она линейная регрессия), например, мы можем пробовать строить на каждом баре и попытаться предсказать что дальше будет происходить при условии что мы используем такую модель. В реальности могут использоваться более сложные модели, но все они делают фактически одно и тоже — пытаются описать наблюдаемый случайный (в смысле того, что мы не можем точно до копейки посчитать/предсказать будущие значения, а то и вовсе не можем ничего предсказать, т.е. в наблюдаемом процессе присутствует случайная компонента) процесс.

Теория вероятности, математическая статистика (и другие подмножества математики) изучают случайные процессы (процессы в которых присутствует случайная компонента, процессы целиком состоящие из случайной компоненты), позволяют оценивать случайную и неслучайную компоненту наблюдаемого процесса (в рамках используемой модели), позволяют строить и описывать модели того, как развивается процесс, на что он похож, описывать характеристики и строить на основании этого какие-то прогнозы. И тут главное не потерять связь с реальностью, не перестать видеть за цифрами реальный мир, ведь теория вероятности, математическая статистика это про вероятности каких-то событий в рамках выбранной модели, в реальности все может быть совсем по другому, неожиданно по другому.

П.С.: В качестве прототипа был использован кусок котировок BTCUSDT (для удобства график цены был смещен вниз), построена линейная регрессия (в результате получено уравнение y = 5.33*x) и в качестве случайной компоненты e были взяты остатки регрессии.