Прогноз! Не так все просто как кажется на первый взгляд

Недавно я опубликовал пост «Прогнозы! Что стоит знать и на что обращать внимание?!», где писал о моделях, почему они не способны точно предсказывать будущее, и почему любое предсказание, прежде всего, должно содержать оценку вероятностей различных исходов, а лучше закон распределения вероятности.

В этом посте мне хотелось бы взглянуть на проблему прогнозов немного с другой стороны. Но прежде еще раз кратко, о вероятности и ее значении. Большинство прогнозов  не содержит информации о вероятности, либо эта вероятность дана в очень размытой форме.  Например, можно увидеть такую формулировку: «Я оценивая шансы на успех в этом мероприятие, как достаточно высокие». Но что это значит – «достаточно высокие»? Кроме очевидного встречного вопроса: «Как вы оцениваете шансы этого успеха в численном выражении?», необходимо еще учесть контекст предмета прогноза. Легко понять, что в контексте выбора между кардинально различными ситуациями: от крайне плохого сценария — потерять все вложения, до крайне положительного — получить прибыль в 300%, шансы на успех 3 к 1 будут трактоваться простыми словами – игра стоит свеч. Но что, если прогноз дается в условиях крайне негативных. Например, при ведении боевых действий командованию необходимо принять очень сложное решение с военной точки зрения. И их оценка шансов на успех 1 к 3. И несмотря на, это все равно будут «достаточно высокие» шансы, потому что все остальные куда как хуже.  Эти два простых примера наглядно демонстрируют, что размытые формулировки необязательно связаны с желанием прогнозистов «оставить себе пути к отступлению», они могут быть объяснены вполне разумными внешними факторами и обстоятельствами. Итак, оценка вероятности в числовом выражении полезна в том, что она снимает различные трактовки и существенно понижает значимость контекста.

Но есть еще одна интересная проблема. Предположим, что прогнозист дает прогноз, в котором указывает, что вероятность, с которой он сбудется, составляет 70%. Приходит время исполнения прогноза, и тогда  возможны два сценария:

• Он сбылся, и многие скажут, что он был прав
• Он не сбылся, и тогда многие будут говорить, что он ошибся

Понятное дело, что под многими я имею в виду большинство обычных людей, которые плохо знакомы, а зачастую не знакомы совсем, с теорией вероятностей. Конечно, он в обоих случаях был прав. Но вот насколько он был прав, можно понять только одним образом. Если бы по предмету его прогноза можно было поставить эксперимент: сделать 1000 измерений и в этой тысяче — 700 давали тот же результат, о котором писал прогнозист, а 300 нет. Тогда получалось бы, что он абсолютно прав. В противном случае, можно было бы измерить величину ошибки его прогнозов. Однако, очень часто у нас нет такой возможности. Такие вещи можно проверить в естественных науках, но крайне сложно в социальных или в предсказывании погоды. Процесс сопоставления прогноза по вероятности с реальными результатами называется калибровкой. Но даже с калибровкой не все так гладко. Предположим, что один прогнозист всегда дает вероятность по своим прогнозам от 40 до 60%, а другой от 5% до 20% и от 80% до 95%. Несложно догадаться, что калибровка в для первого будет существенно менее значима, чем для второго. При этом будет совершенно очевидно, что если у второго калибровка будет подтверждать данные его прогнозов, то это будет говорить о крайне высоком уровне прогнозиста.

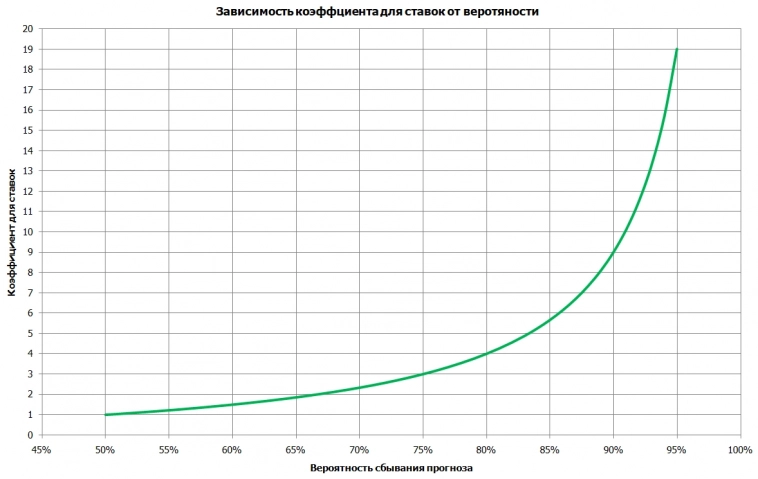
Очень часто можно увидеть, что человек делая прогноз дает вероятность его исполнения, которую берет с потолка. К сожалению, в нашей среде это не редкость. Какой лайфхак можно было бы применить, чтобы вывести человека на чистую воду, или хотя бы самому понять – разбирается прогнозист в вероятностях или нет?  Можно предложить ему заключить пари. Цель пари не в самом факте его заключения, а в желании понять какова будет предложена ставка, а вернее коэффициент.  Логика здесь достаточно проста: если вероятность 50 на 50, то коэффициент должен быть равен 1, 60/40 – 1,5, 75/25 – 3, 80/20 – 4, 90/10 – 9, 95/5 – 19 (график коэффициентов приведен к настоящему посту).  Или вы можете сами предложить ему такие коэффициенты и посмотреть, как человек на них будет реагировать. Конечно, он может сразу отказаться и это еще не значит, что он не прав. Но если он решит с вами поторговаться, то будет интересно понять насколько он сам оценивает ту вероятность, которую написал. Зная коэффициент можно получить вероятность прогноза, рассчитав его в обратном направлении.


Простой пример. Вы прочли, что вероятность прогноза по росту акций компаний в течение месяца составляет 80%. Тогда вы пишите аналитику предложение заключить пари: «Ставлю 10 000 рублей, что Ваш прогноз не сбудется, но если выиграю я, то вы мне заплатите 40 000». Прогнозист оказался азартным и пишет вам ответ: «Готов принять Ваше предложение, но в случае проигрыша я вам также заплачу 10 000». Это значит, что в своем прогнозе он уверен не в соотношении 80 на 20, а 50 на 50. С другой стороны, если он наоборот поднимет коэффициент, то это будет выглядеть странно. То есть его уверенность в правильности существенно выше, чем был дан прогноз. Еще раз повторюсь, что цель такой проверки не в заключение самого пари, а желание понять, человек понимает основы теории вероятностей, или просто пишет для красного словца, чтобы его мысли приобрели вес в глазах его читателей.

Конечно, цель поста не научить вас грамотно троллить незадачливых псевдо-аналитиков, а показать, что прогнозы дело важное и не такое простое, как для тех, кто их пишет, так и для тех, кто их читает. Понимание базовых принципов крайне полезно, и помогает не наломать дров.