Частоты на фондовой бирже. Часть1.

Как можно представить разложение Фурье и Вейвлеты? Не вдаваясь в математику, в которой я прямо скажем не большой специалист, это представление временного ряда в других системах координат. 

Вот например такой ряд — немножко похожий на котировку застрявшей в боковике акции.


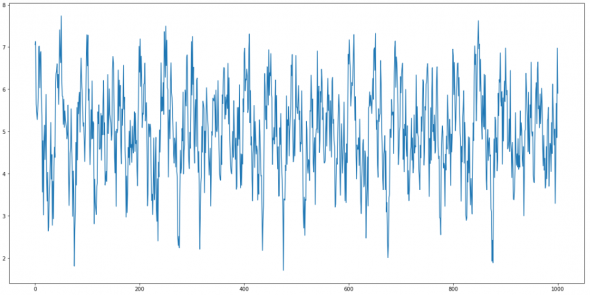
Опытный трейдерский глаз конечно сразу заметит что на котировку это не очень похоже. Но я сейчас не об этом, я о том что этот внешне беспорядочный ряд раскладывается на 4 гармоники (плюс розоватый в самом низу-шум). 


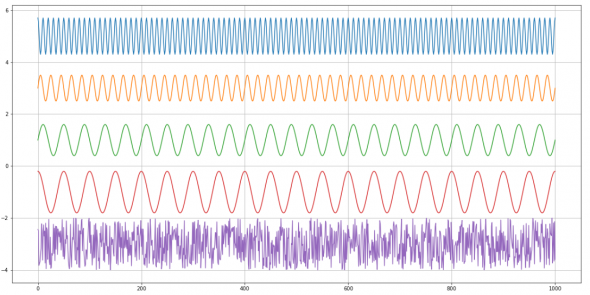
И вот разбивка в частотно — амплитудном разрезе: 



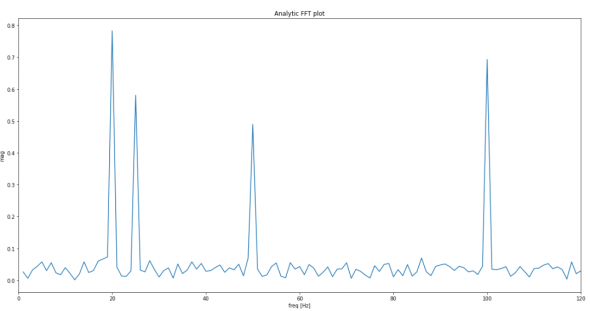
Все четко, амплитуды, частоты совпали. Скажем спасибо Фурье 2 раза.
А теперь давайте представим что каждая гармоника была в определенный период времени, добавим немножко тренда, делаем ряд не стационарным.



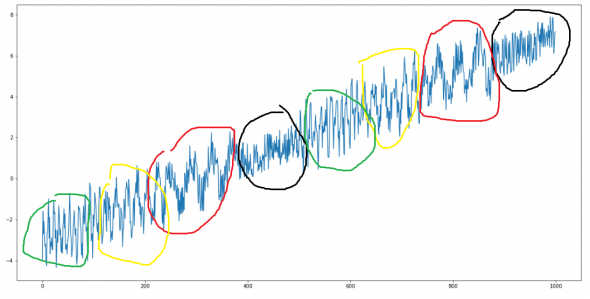
Зовем на помощь Фурье и получаем какую то кашу:



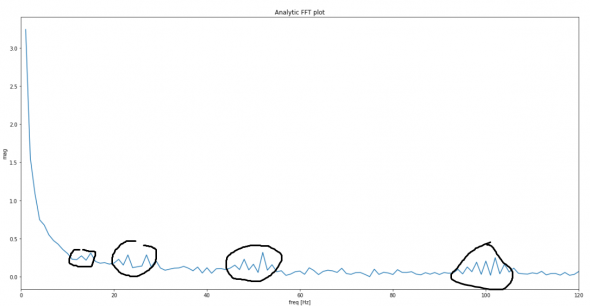
Легкой, уходящей зыбью можем наблюдать, ранее так хорошо выраженные частоты. И главное, мы совершенно непонимаем, когда, какие частоты преобладали по времени. Фурье загоняет амплитудно — частотную картинку временного ряда в общую кашу и самодовольно хымыкает — «кушать подано». 
Но, как говорится спасибо этому дому, пойдем искать следующий. 

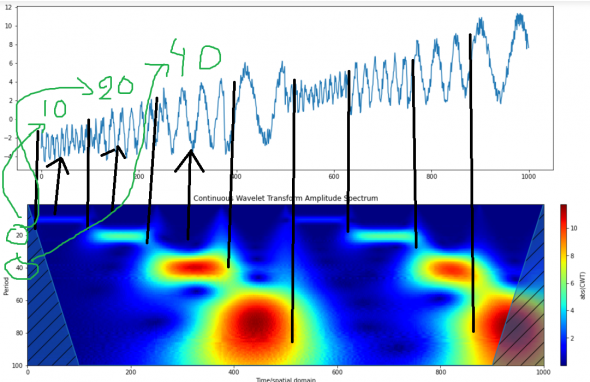
Тут мы видим когда, какая гармоника, с какой частотой и амплитудой присутствовала. А называется все это вевлет преобразованиями. В отличие от синусойд-косинусойд старичка Фурье, тут используются вейвлет функции, который локализованы не только по частотам, но и по времени, что позволяет получить информацию по временному ряду в разрезе: амплитуда-частота-время. Говорим спасибо вейвлетам.

Но нас конечно интересует не это, нас интересует как бы вот это все да на фондовой рынок. Так что берем реальные котировочки, загоняем в вейвлет преобразования и получаем что то вроде:


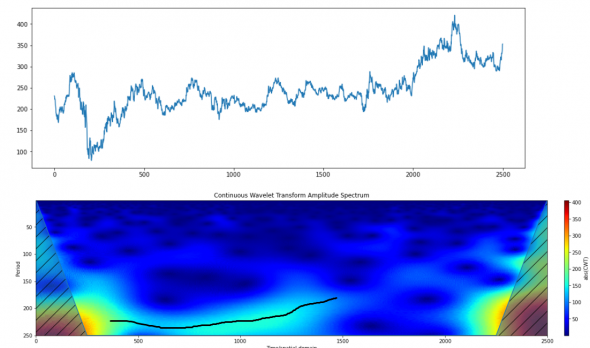
… тоска зеленая… И поверьте, это еще лучшее из тех отечественных голубых фишек что я смотрел. Фишка-Роснефть, как сами понимаете.  
Где четкие линии?! Ну что поедать, тренды и шум враги вейвлетов.
Кстати так выгладит скалеограмма случайного блуждания c добавлением тренда:

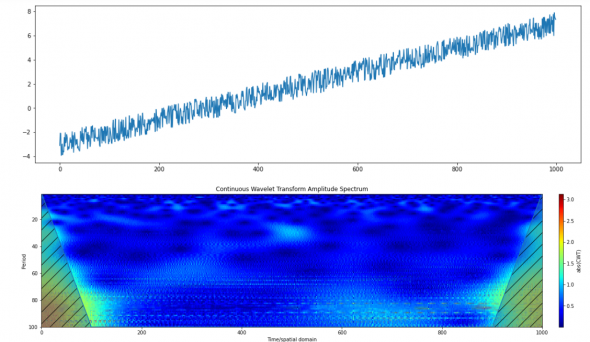
То есть как бы фондовый рынок не случайное блуждание, но как то не очень далеко от него ушло. Глобально если смотреть. 

Ну а теперь давайте возьмем тот участок котировок Роснефти, где присутствовала гармоника, с периодом 220. Смоделируем гармонику и наложим ее на на котировку, так сказать из любопытства. Смотреть надо не на амплитуду, а на частоту


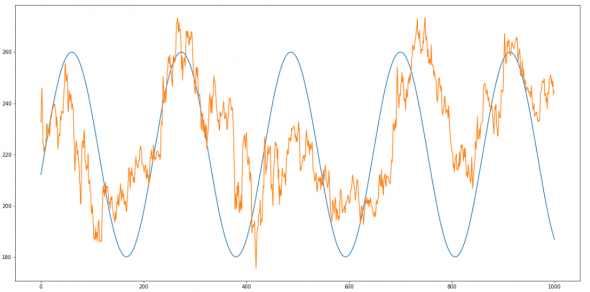
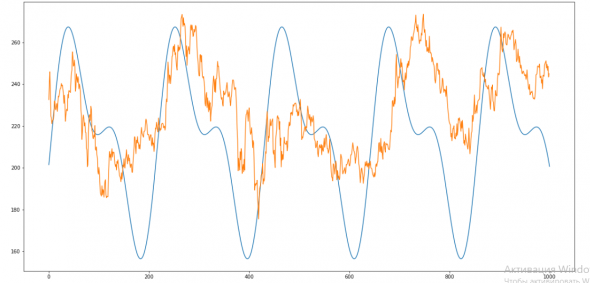
Кроме того можно увидеть еще одну гармонику в этот же период. Добавлем: