Теория и Практика Дельта-Хеджа

Для того, чтобы продать волатильность, нам необходимо продать стрэддл — этим, мы полностью избавляемся от чувствительности к направлению движения цены, оставляя при этом чувствительность к «волатильности»… Чтобы не запутаться, обозначим первую волатильность за IV (Implied Volatility) и будем считать  её заранее известной и эффективной. 


Если бы рынок был монеткой и выходил бы на экспирацию двумя возможными вариантами {+IV, -IV }, то результатом продажи нашей опционной конструкции был бы ровно 0, в силу равенства IV=RV. Но рынок выходит на экспирацию через «тренды» и «пилы», которые выводят Базовый Актив в том числе далеко за ± IV, и в том числе и в ноль.  В результате, конечное отклонение от ± IV  и, соответственно, риски, которые мы принимаем при продаже стрэддла, составляют приблизительно :



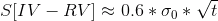
где S — СКО, RV ( «реализованная волатильность»)   - отклонение цены на экспирацию, t — время до экспирации, а сигма0 — величина шага движения цены. Это уравнение можно получить численно, а можно, взяв интеграл по соответствующему распределению Гаусса (аналитический вариант).  


Теперь рассмотрим наш стрэддл несколько повнимательней:



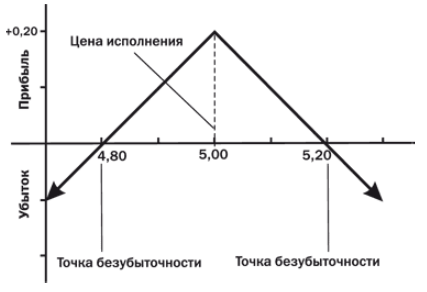
Наш стрэддл имеет две длинные ноги, имеющих дельту ± 1  (для простоты считаем тетта=0), и легко хеджирующихся такими же фьючерсами, и одну особую точку — центральный страйк, для которого дельта (первая производная по цене) = 0, но гамма (вторая производная по цене) = -20, и она уже фьючерсами никак не хеджируется. Для простоты, конечно, мы полагаем, что цена изменяется как-то дискретно с некоторым шагом H (10 центов на рисунке).

И как бы мы не хотели захеджировать эту особую точку — мы этого сделать не можем, так как контр-инструмент, то есть фьючерс, не обладает никакой гаммой и не в состоянии её захеджировать (хеджирование опционами мы не рассматриваем). При этом, сколько бы наша дельта не стремилась здесь к нулю, из-за существования гаммы наша конструкция все равно остаётся чувствительной к изменению цен БА*.


* В этом смысле, стоимость опциона это отнюдь не стоимость его дельта-хеджа. 



Теперь, чтобы рассчитать предельную (конечную) эффективность идеального дельта-хеджирования, нам нужно всего лишь рассчитать неопределённость или риски, связанные с гаммой. Для чего, сначала рассчитаем среднее время пребывания нашего стрэддла на ЦС:




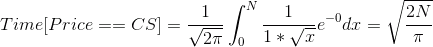
где N — время до экспирации в единицах интервала рехеджа, равное числу изменений цены или числу рехеджей.


Полученное время есть, в свою очередь, случайная величина, для которой, можно записать:






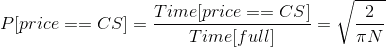
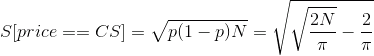
(вышеприведенные результаты подтверждены моделированием)


Теперь, поскольку мы полностью захеджировали риски в иных ситуациях, то оставшиеся после дельта-хеджа риски составят: 



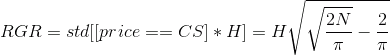
где RGR — остаточный гамма-риск (Residual Gamma Risk), H — шаг дельта-хеджирования, N — количество шагов до экспирации.



Переходя к непрерывному случаю и, учитывая вид 2-ого члена в разложении Тейлора, получим выражение для непрерывного остаточного гамма-риска :






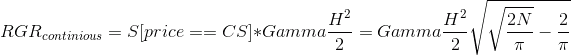
Таким образом, мы получили теоретический предел сжатия рисков при помощи дельта-хеджирования.  Изобразим полученную зависимость графически:



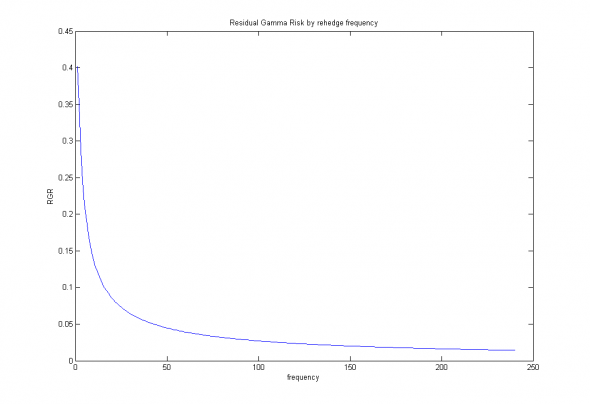
Иллюстрация. Зависимость остаточных рисков от частоты дельта-хеджирования. 


Теперь сравним полученное теоретическое значение с экспериментальным, захеджировав по 10 000 стрэддлов, длительностью 15, 60 и 240 шагов (дней) при помощи одного из моих алгоритмов хеджирования, при априорно заданных IV=H=1.



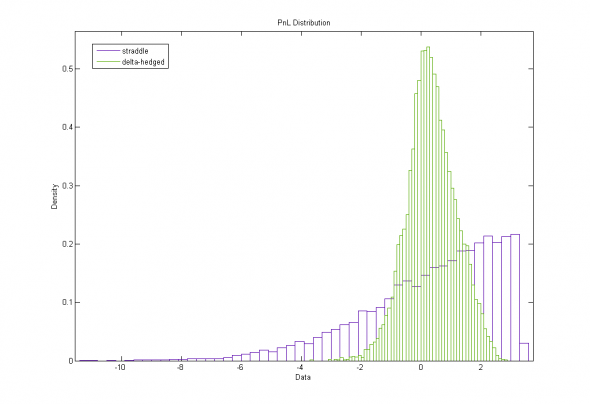
Рис. 1. Стрэддл на 15 дней, 10 000 симуляций :

Теоретический Риск стреддла = 2.32 ,  Эмпирический результат = 2.24

Остаточный Гамма-Риск (теория)  = 0.78, Эмпирический результат =  0.81

 

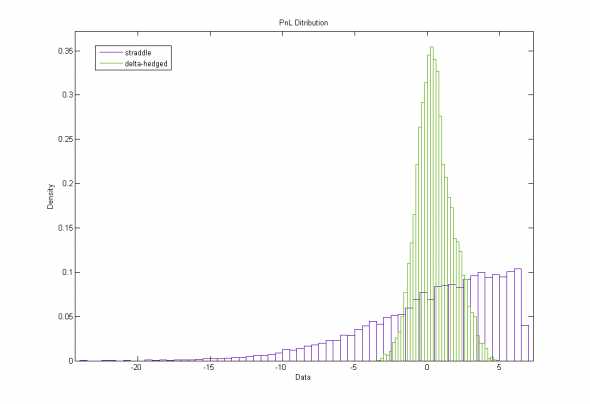
Рис. 2. Стрэддл на 60 дней, 10 000 симуляций :

Теоретический Риск стреддла = 4.64, Эмпирический результат = 4.63

Остаточный Гамма-Риск (теория)  = 1.18, Эмпирический результат = 1.26



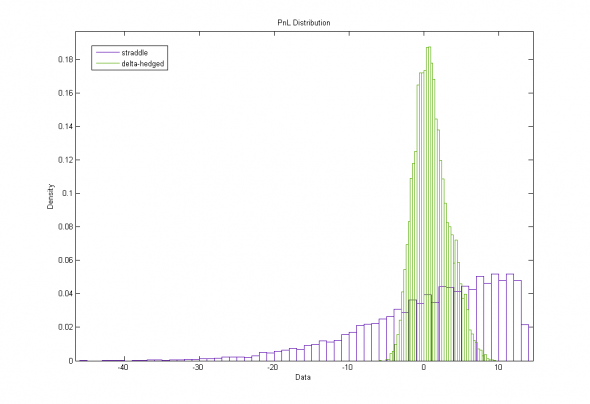
Рис. 3. Стрэддл на 240 дней, 10 000 симуляций :

Теоретический Риск стреддла = 9.29, Эмпирический результат = 9.22

Остаточный Гамма-Риск (теория)  = 1.71, Эмпирический результат = 2.29