Оценка качества прогноза моделей и цена опциона. Часть 2. Эврика!
В продолжение этого поста smart-lab.ru/blog/547833.php. Готового решения не нашлось, так что пришлось изобретать свой велосипед. На мысль натолкнул комментарий Кирилла Браулова smart-lab.ru/blog/547833.php#comment9870122. Действительно, почему бы нам вместо ошибки не считать модельную вероятность фактической реализации. Вероятность конкретной цены – около нуля. Ок, можем взять не точку, а некоторую окрестность слева и справа. Тогда распределения можно будет сравнить по сумме/среднему вероятностей фактических реализаций за большое количество экспериментов. Вроде задача решена. Но почему бы не пойти дальше…
Мы можем разделить прогноз на n равновероятных интервалов, например, 10 или 100. Для этого рассчитаем квантили с шагом 0,1 или 0,01. И проверим в какой интервал попала фактическая реализация. И так для всех экспериментов. Пример на картинке
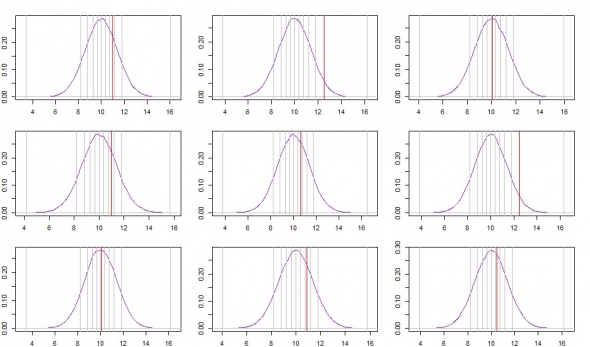
И, наконец, посчитаем количество попаданий в каждый интервал. Ну а дальше все просто. Если мы очень хорошо прогнозируем, то количество попаданий в интервалы будет равномерным. А в качестве метрики будем считать критерий хи-квадрат.
Получилась метрика, которая не только позволяет сравнивать качество прогноза нескольких моделей, но и получить абсолютную оценку качества прогноза. Т.е. мы можем оценить насколько наша модель соответствует реальности)
Всем поучаствовавшим в предыдущем обсуждении большой респект, особенно Кириллу!














Если не сложно, напишите про эти тесты топик. Ваши объяснения очень доходчивые.