Московская опционная конференция.

30 марта, из оставшихся в живых и вновь прибывших опционных трейдеров, состоится шоу. Наша любимая конференция, любезно организованная фирмой Дерекс (не путать с Дюрекс). И, естественно, ваш покорный слуга, скажет там несколько слов.

О чем бы я хотел поговорить? О том, о чем вы попросите. Однако, у меня есть план. И я хотел бы поделиться с публикой СЛ этим, пока зеленым, планом.

В общем, хотелось бы рассказать об использовании опционов совместно с портфелем акций. Написать много дифуров и их решений. Но, думаю, это сложно. Однако, первую часть выступления надо будет посвятить теории. С простыми примерами. Распределение, случайность, откуда переменные в БШ, почему это работает и т.д. Во второй части я приготовил портфель. В конце января я запустил стратегию на акциях и опционах и мы разберем что вышло.

Конечно, это сложно. Менять стереотипы. За 30 минут это не возможно, но у нас будут пончики со сладким кофе, и мы все обсудим.  Если есть пожелания и вопросы, которые надо поднять, то милости просим задавать их в комментариях.

И что бы топик не был пустым, закину задачку на вероятности и способ ее решения.

Возьмем ценовой ряд и изменение цены за 100 периодов времени. Какова вероятность того, что цена останется на месте и сколько это стоит? Человеческим языком. У нас есть 100 тиков, или 100 квадратиков ренко (как у Московский Лоссбой ). Какова вероятность, что из 100 кубиков, 50 будут зелеными? Ну а если 50 зеленых, то где то есть 50 красных, цена не ушла и наш проданный стреддл принес нам сколько?

Ну и давайте рассуждать на уровне школьной программы про комбинаторику. Первое, что понятно, это вероятность поймать 50 красных кубиков подряд из 100 кубиков. (1/2)^100. Второй вопрос. Сколькими способами можно расположить 100 кубиков в одну строку. Это как, за сколько попыток вы откроете замок на чемодане с кодом из 4 цифр. И этому учили в школе. И называется это факториал. Это 1*2*3*4…*n, помните? С помощью его мы найдем биномиальный коэффициент

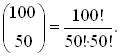
Вероятность, что цена вернется

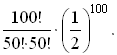
Теперь, или эксел или спец таблицы=0,07959.

В общем, на этом школьная программа и заканчивается. Там нам дают много знаний, но так, что бы мы не могли ими воспользоваться. Иначе, мы ни когда не запишемся на курсы по трейдингу к Герчику, не будем рисовать уровни и искать фигуры в волнах вульфа. Сами подумайте. Какой рациональный человек будет 1*2*3*…*100 перемножать в уме. Поэтому, такое знание быстро вымывается из мозга. Но есть простое решение. Называется оно формулой Стирлинга и рассчитывает n!

Я не стану лукавить. Эту задачку не я придумал. Ее можно найти и в лекциях Кирилла Ильинского и на просторах интернета. В данном случае я делаю копипаст с задачи по подбрасыванию монетки http://termist.com/bibliot/stud/50_prob/18_1.htm  И наши 100 квадратиков ренко, соответствуют 100 монетам с орлами и решками. Потому что природа явления одна и та же. Ну и решение через формулу Стирлинга выгладит так:

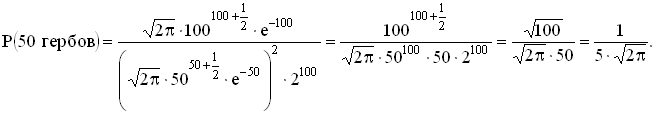
Вот это формула БШ. Почему? Потому что цена опциона =1/(2Пи)^0.5*цена БА*волатильность*время^0,5. При страйк=ценаБА. Можете проверить на рынке. Собственно говоря, вот за эту вероятность, что цена останется на месте, вам и предлагают премию опциона. Входной билет в эту игру. Ну а теперь, может быть 200 тиков, 1000 тиков, волатильность меняется, цена меняется. В опционе еще меняется время. 1 раз подбросили из 100, осталось 99, вероятность поменялась. Вот такие примеры мы и будем разбирать на конференции

Если интересно….