Информация к размышлению
О длине временного ряда технических индикаторов
Одним из ключевых вопросов применения большей части индикаторов технического анализа является выбор и настройка длины их временного ряда.
Логика здесь простая. Если единиц информации, назовем это далее – « бит информации « (к примеру, тиков цены), которую пытаемся прогнозировать мало, то мы находимся во власти опасения, что эта величина или событие — были случайными. В противном случае (если количество единиц анализа велико), то нам жалко и ресурсов их добывания, и мы понимаем, что временная (ударение на « нн ») точность их « приведения « к моменту начала исследования, уже другие. Это тоже, что сравнивать мокрое с теплым.
Более того, по Н. Талебу: " сложные системы строятся на информации, и передатчиков вокруг нас куда больше чем мы замечаем. Это явление мы назовём казуальной непрозрачностью. С причинами и следствиями нам разобраться сложно. Отчего традиционные методы анализа, не говоря о стандартной логике непригодны. По этой причине, как я уже говорил предсказать конкретные события почти невозможно. Причина кроется именно в казуальной непрозрачности… , а также нелинейности....» [Н.Талеб, Антихрупкость, стр. 97].
Обычный временной ряд последовательности натуральных чисел – линеен и с позиций поиска « экстремальных « точек, не имеет смысла. Так, по определению « натуральными числами называются числа, которые используются при счете или для указания порядкового номера предмета среди однородных предметов ».
Даже уже и в этом определении – видится подвох. Так как интуитивно, и по Талебу, мы не можем с уверенностью утверждать, что цена, например 7 порядкового номера, « однородна « 2 или 3 или 1-й. События, происшедшие на бирже, в период между ними нам не известны в полной мере, т.е. казуально непрозрачны.
А коли так, то и нет оснований считать цену 7 и любого другого порядкового номера однородными. Именно поэтому, в такой постановке, попытка определить « оптимальный временной ряд » — не имеет решения. И различные практики визуализации (определения визуально начала или конца, искомого временного ряда) предполагают другую логику авторов.
С нашей точки зрения, одной из таких позиций могут быть следующие рассуждения. Если принять, что каждый бит информации нелинейного свойства, то первым числом построения нелинейности, является 5-ка. То есть количества « членов » анализируемого ряда минимально не может быть менее пяти (то есть всегда бывают пять точек, через которых проходит единственная кривая второго порядка). Конечно в варианте теоремы Безу (алгебраическая геометрия), все « несколько « сложение, но нам важна практическая сторона дела.
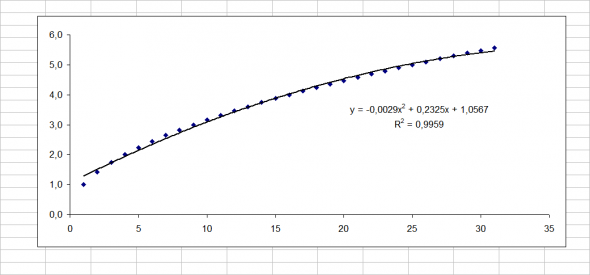
Далее, приближением «нелинейного рассеяния ценности» изучаемой последовательности можно принять, степень ½ — квадратный корень из анализируемых значений. И исследование кривой ( рис.1 ) на экстремум ( первая производная ), дает искомое значение ряда в районе 40-ой точки. То есть с точки зрения исследования информационной « нелинейности » натурального ряда — оптимальное значение лежит в районе 40-вой точки. И если Вы работаете с 5-ти минутными тайм фреймами, желательно ориентироваться на трехчасовый данные (40*5/60=3,3 часа ).
Был приятно удивлён, что остались ещё читатели блогов в духе аля Николая ( фамилию уже забыл, Старченко вроде). Писал больше для себя, хорошо, что ещё кто-то занимается...
А богатым Талеб стал, когда в 2004 просёк безумные риски ипотечной пирамиды. И три года в убыточной позиции против этой пирамиды дожидался своего триумфа.
Все биржевые исследования Талеба нацелены на ниспровержение любых квази-научных (других не бывает!) попыток поймать природу рынка в математическую модель.
Так что ссылки автора на Талеба совершенно неуместны.
«Все биржевые исследования Талеба нацелены на ниспровержение любых квази-научных (других не бывает!) попыток поймать природу рынка в математическую модель».
Помните, что это относилось только к гипотезе эффективного рынка?
Y**2 — X = 0?
Она проходит через все точки.
В рынке встречаются квадратичные зависимости, пытаюсь понять Ваш случай.
Может прояснится, если расскажете, как получили тот полином.
Близость рынка к случайному блужданию порождает квадратичную зависимость (корень квадратный) высоты свечек от таймфрейма, как тенденцию — вспомните про пьяного моряка из бара, это же классика.
Но есть и другие, малоизвестные квадратичные зависимости.
Стохастический: Определение процесса, определяемого рядом наблюдений.
Вникнете в эти простые слова!) тобишь какой ряд наблюдений такой и процесс. поменяшь ряд получишь новый! процесс .
ну как то так )
Устранить избыточность информации во временных рядах или ограничить необходимую для работы длину ряда — интересная задача. В ее решении я радикально расхожусь со многими, но оценка ТС (число, но не способ) мне нравится. У меня оптимум будет повыше в разы, но не на порядки.
На SL, насколько я заметил, это интересно было только единицам. Раз в несколько лет они появлялись и скрывались. Большинство пытается идти проторенными магистралями.
К абсолютным константам я отношусь с уважением. Читал как-то, что изменись какая-то физическая константа в шестом знаке и наша Вселенная перестанет существовать.
Пример «оптимальной» константы — число «е», основание натуральных логарифмов, является оптимумом по чисто информационным основаниям (почти по теме ТС), между длиной алфавита и длиной или количеством чисел в этом алфавите.
Можно в интернете найти по контексту «оптимальная система счисления».
Это Физика.
а я имел в виду рыночные системы. это другая вселенная. существующая по другим законам)))стохастическим.
без обид. как то так чтоли)
«а я имел в виду рыночные системы. это другая вселенная. существующая по другим законам)))стохастическим.»
На этот счет есть и другие мнения, например, Атамана.
Конечно, без обид.
Потому попытки «предсказать» здесь хоть что-то, вызывают в лучшем случае улыбку… Это невозможно, по крайней мере в извесной нам вселенной. И в этом я вами полностью согласен.
С бестами и регардами,
Алекс»
"… Еще одно определение: Явление, когда целое определяет поведение своих частей (что отличает биологические системы и фондовый рынок) есть одно из отличительных свойств биологической системы и названо омникаузальностью, в противоположность партикаузальности, т.е. детерминации целого со стороны его частей, характерной для физико-химических систем."
как то так…
«Мастером себя не считаю но, могу заметить, что есть резон мессадж Akelo перечитать еще раз, он там оооооочень подробно фсе описал, ИМХО.
Попробую немного другими словами.
То, что мы видим на базаре, выглядит как перемежающиеся зоны консолидации + переходы между такими зонами. То есть, по-простому, это фсе выглядит как траектория частицы при ее движении между множественными зонами притяжения (аттракторами).
Фсе это (ИМХО) наиболее красиво описывается формулами Волновой Оптики (как движение света в средах с переменной плотностью), но может быть описано, так же, как траектория частицы между аттракторами, что несложно для большинства челов, с вопросом знакомых… Ляпунова фсе читали.
Так вот, когда частица движется между аттракторами, то Марковость фсего этого, вызывает большие сомнения, поскольку нет уверенности в сохранении эргодичности (когда среднее по времени равно среднему по реализациям) и вообще под вопросом, есть ли этот процесс — порождение случайной функции. Акело про это написал: «Пока идет направленной движение процесс сильно отличается от марковского...».
Затем, когда частица “захвачена” аттрактором в зоне притяжения, то мы видим процесс практически точно Марковский. Акело про это написал: «сокращается глубина памяти возрастает марковость, вплоть до момента „касания“ резиста» .
Поэтому, “стандартными методами” описать это НА ВСЕЙ ДИСТАНЦИИ, вряд ли получится.
С бестами и регардами,
Алекс „
"… Мы это с ней дискутировали по почте, помнится в 1995… Очень толковая тетка, рекомендую. Кроме того я считаю, что свинг трейдинг всегда основывается на pattern recognition.
Для начала гляньте книжки Arthur A. Merrill «Behavior of Prices on Wall Street», «Bear Market Characteristics».
Им был предложен 5-и точечный метод и 18 типовых паттерн.
Есть еще один удивительный человек, Clyde Lee,
предложивший 4-х точечный метод и 9 паттерн.
Но он, к сожалению, книжек не пишет и с ним можно только по е-мейлу общаться.
Кроме того, помните Дж. Сороса и его книгу «Алхимия финансов»? Он там немного написал про самоусиливающиеся процессы на фондовом рынке.
Чем не идеология для трейдера: В начале такого процесса (когда все считают,
что тренда нет) — ты торгуешь тренд. В стадии «финального вздутия» (blowoff) --
ты встаешь на противоположную сторону (когда все считают, что есть мощный тренд).
А сам процесс дифференцируешь по 3-м точкам 4-х или 5-и точечной модели.
Кроме того, есть совсем простые модели для свинга."
«А вообще-то, не нами замечено, что торговать
паттерны — ну о-очень прибыльное занятие.
Их вполне просто формализовать и просчитывать.
Приблизительно 75% входов приносят прибыль
уже через 20 минут.»
«Вот рынок и „рисует“ одни и те же формации год за
годом. А раз это статистика, то можно строить вероятностные функции и математически строго расчитывать риски, реварды и стопы.
Поверьте, работать „игральным автоматом“ — весьма интересное занятие.»
ну вот так… информация к размышлению а вообще спасибо, освежил память.
Были и отличия, возможно Атаман не все озвучил — математика и физика рулят на бирже, некоторые направления за 20 лет бурно развивались, одни китайцы могут просто количеством исследований задавить.
Прорыв точно будет, может уже и состоялся, но остался закрытым.
Про формации и статистику.
В таблице Менделеева уже под 118 формаций, кто-то считает, что это предел, но кирпичиков, из которых они строятся совсем мало и правила формирования формаций или разрешенные конфигурации существуют.
Распознать эти кирпичики (в рынке их всего единицы) можно (попробовать по аналогии) и для этого распознавания нет необходимости иметь 50000 точек. Математика и физика, а не статистика, должны подсказать, что искать, у Атамана же были мысли.
И, естественно, это распознавание будет каким угодно, «стохастическим», «топологическим», «интерполяцией» ..., но точно не «детерминированным».
У Дж.Трефила в «200 законов мироздания» есть совершенно изумительное Введение. Природа науки на 30 страниц
О науке.
Наблюдения или эксперимент?
Закономерности.
Гипотеза.
Предсказание.
Большой цикл.
Роль законов природы.
Наука в ХХ веке.
Рекомендую, мозги могут начать работать по-другому.
Да, еще обратил внимание, что Талеб, Атаман и я понимали разницу между «каузальный» и «казуальный» и выбор делали однозначный. Это принципиальный подход и не анекдот.
А вот анекдот.
Что должен отличать настоящий интеллигент?
Гоголя от Гегеля,
Гегеля от Бебеля,
Бебеля от Бабеля,
Бабеля от кабеля,
кабеля от кобеля, а кобеля от суки.
Спасибо. гляну.
Если у вас есть точки, сгенерированные реальным физическим процессом (геологической историей, биржевыми спекулями и т.д.), то для интерполяции этих точек вы можете придумать миллионы замечательных моделей. Но даже между этими экспериментальными точками, не говоря уж о выходе за область их определения (в будущее), все ваши модели будут попадать пальцем в небо. Кроме одной, сложность которой может превосходить все доступные человечеству ресурсы.
Дело в том, что природа, механизм всех подобных процессов меняется постоянно.
Полностью согласен с Вами — ресурсоемкость модели — необычайно важный и реальный фактор.
Два совершенно наивных способа дали мне примерно одно значение. Через несколько лет я узнал ответ — он был близок к моему.
Поэтому мне интересны разные варианты по проблеме, затронутой ТС, какими бы странными они ни казались на первый взгляд.
При первом выборе — действительно требуется много данных,
при втором, когда признаете наличие причинно-следственных отношений и закономерностей, точек требуется существенно меньше, но эти закономерности еще надо «вычислить-нафантазировать» (наука нам в помощь), а потом суметь найти в существенно меньшем объеме данных с приемлемыми точностью и временем.