25 февраля 2018, 18:50
Формула для расчета вероятности выхода опциона в деньги
Чтобы окончательно поставить точку в вопросе о том, почему дельта опциона не равна вероятности выхода опциона в деньги, давайте просто посчитаем эту вероятность.
Для экономии места и времени я буду использовать кое-какие обозначения и преобразования, которыми я пользовался в посте "Функция нормального распределения в формулах стоимости опционов".
Рассмотрим логнормальное случайное блуждание:
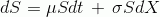
где dX — Винеровский процесс.
Определим вероятность того, что цена из начальной точки S во время t окажется в диапазоне от a до b во время t':
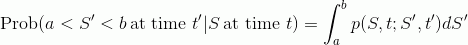
где функция p(S,t;S',t') — это функция плотности вероятности перехода. Т.к. она связывает переход цены из одной точки в начальный момент времени в другую точку в конечный момент времени, то она удовлетворяет прямое и обратное уравнение Колмогорова. Т.к. нас интересует вероятность выхода в деньги в конечный момент времени, мы используем прямое уравнение Колмогорова:
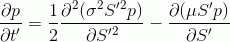
Значение цены в начальный момент времени нам известно, поэтому мы можем сформулировать начальные условия для решения уравнения (используя дельта функцию):
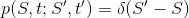
Решением уравнения будет:
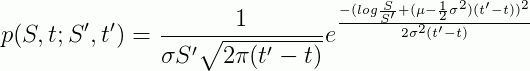
Рассматриваем вероятность выхода опциона call в деньги, поэтому интегрируем ее от страйка и выше:
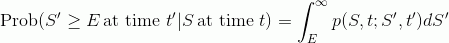
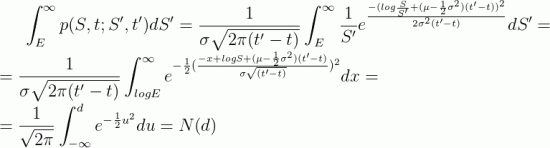
где
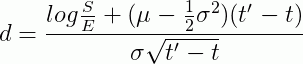
Похож ли результат на дельту опциона call N(d1)? Похож, но есть и отличия. Первое — это знак перед 0.5*sigma^2, он противоположный. Это значит, что вероятность выхода в деньги гораздо больше похожа на N(d2), чем на дельту, равную N(d1).
Но есть и еще одно довольно существенное отличие. В дельте опциона у нас безрисковая ставка, а в формуле вероятности выхода в деньги — тренд базового актива.
И это, во-первых, совершенно логично, а во-вторых, делает приравнивание дельты к вероятности выхода опциона в деньги довольно грубой ошибкой, если до экспирации далеко и тренд базового актива может еще внести ощутимый вклад.
Функция нормального распределения в формулах стоимости опционов
Для экономии места и времени я буду использовать кое-какие обозначения и преобразования, которыми я пользовался в посте "Функция нормального распределения в формулах стоимости опционов".
Рассмотрим логнормальное случайное блуждание:
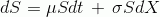
где dX — Винеровский процесс.
Определим вероятность того, что цена из начальной точки S во время t окажется в диапазоне от a до b во время t':
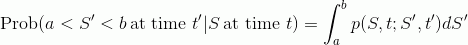
где функция p(S,t;S',t') — это функция плотности вероятности перехода. Т.к. она связывает переход цены из одной точки в начальный момент времени в другую точку в конечный момент времени, то она удовлетворяет прямое и обратное уравнение Колмогорова. Т.к. нас интересует вероятность выхода в деньги в конечный момент времени, мы используем прямое уравнение Колмогорова:
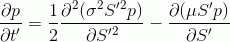
Значение цены в начальный момент времени нам известно, поэтому мы можем сформулировать начальные условия для решения уравнения (используя дельта функцию):
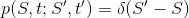
Решением уравнения будет:
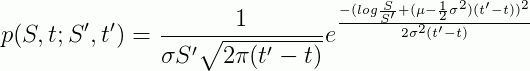
Рассматриваем вероятность выхода опциона call в деньги, поэтому интегрируем ее от страйка и выше:
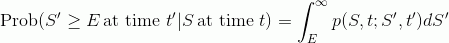
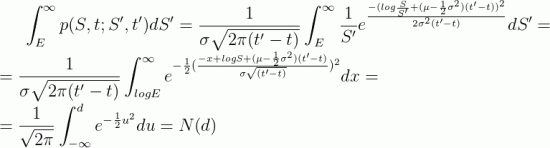
где
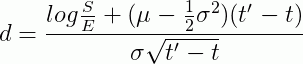
Похож ли результат на дельту опциона call N(d1)? Похож, но есть и отличия. Первое — это знак перед 0.5*sigma^2, он противоположный. Это значит, что вероятность выхода в деньги гораздо больше похожа на N(d2), чем на дельту, равную N(d1).
Но есть и еще одно довольно существенное отличие. В дельте опциона у нас безрисковая ставка, а в формуле вероятности выхода в деньги — тренд базового актива.
И это, во-первых, совершенно логично, а во-вторых, делает приравнивание дельты к вероятности выхода опциона в деньги довольно грубой ошибкой, если до экспирации далеко и тренд базового актива может еще внести ощутимый вклад.
Функция нормального распределения в формулах стоимости опционов
Читайте на SMART-LAB:

Акции для активных трейдеров на март 2026
Цикл статей «Наиболее подходящие акции для активных трейдеров» продолжается. Оценим волатильность рынка в феврале, спрогнозируем динамику Индекса МосБиржи на март, обозначим вероятный курс самых...
02.03.2026

📌 Сегодня стартует сбор заявок на облигации ПАО «МГКЛ» серии 001PS-02
Сегодня, 3 марта, с 11:00 до 15:00 (мск) проходит сбор книги заявок на второй выпуск биржевых облигаций ПАО «МГКЛ» на СПБ Бирже, ориентир доходности выпуска до 29,34% годовых Ключевые...
10:16












если бы процесс был бы нормальным то его крайне просто было бы торговать в профит
кстати любой генератор случайных чисел торгуется элементарно