08 мая 2017, 13:06
Почему анализ Фурье не будет работать на рынке
Для начала вспомним про такую простую функцию, как функция единичного скачка или функция Хэвисайда:
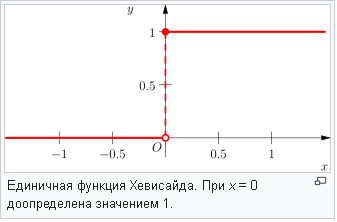
В виде формулы это записывается таким образом.
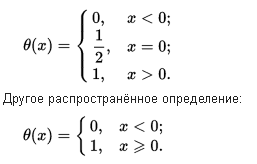
Теперь вспомним, что такое анализ Фурье.
Упрощенно анализ Фурье — это замена функции времени суперпозицией гармонических сигналов, которые заданы на интервале времени от минус до плюс бесконечности, что уже само по себе является проблемой.
Не вдаваясь в тонкости расчетов отметим. что спектр Фурье для функции Хэвисайда можно представить в виде функции ~1/j2пf, которая принципиально содержит все частоты спектра.
Т.е. единичный импульс давно закончился, а гармонические компоненты, соответствующие этому импульсу, существуют и продолжают действовать и длится.
Почему мы вообще взялись за функцию Хэвисайда? Потому что любое изменение цены в момент времени t1 на величину m можно описать как прибавление в момент времени t1 к предыдущему значению цены функции Хэвисайда с весом m. А весь график цены во времени представляет собой не что иное, как сумму множества функций Хэвисайда, соответствующих отдельным тикам графика с весами и знаками приращений цены по этим тикам. Записывать выражение для суммы лень, много суеты по клавиатуре.
Вследствие принципа суперпозиции спектр графика такого цены будет представлять собой бесконечную сумму гиперболических функций ~1/j2пf с разными весами и различным фазовым сдвигом, определяемым временем тика. И тут мы приехали… Мы всегда будем иметь дело с откликом на прошлые значения цены, но этот отклик никоим образом не влияет ни на величину ни на знак, ни на моменты прибавления новых функций Хэвисайда, соответствующих будущим тикам графика.
Если бы график цен был периодическим или хотя бы квазипериодическим, то преобразование Фурье можно было бы заменить рядами Фурье, что дало бы возможность худо-бедно прогнозировать будущее движение цены. Но чего нет того нет… Поэтому про Фурье и гармонический анализ забываем раз и навсегда.

В виде формулы это записывается таким образом.
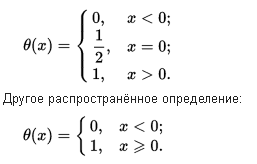
Теперь вспомним, что такое анализ Фурье.
Упрощенно анализ Фурье — это замена функции времени суперпозицией гармонических сигналов, которые заданы на интервале времени от минус до плюс бесконечности, что уже само по себе является проблемой.
Не вдаваясь в тонкости расчетов отметим. что спектр Фурье для функции Хэвисайда можно представить в виде функции ~1/j2пf, которая принципиально содержит все частоты спектра.
Т.е. единичный импульс давно закончился, а гармонические компоненты, соответствующие этому импульсу, существуют и продолжают действовать и длится.
Почему мы вообще взялись за функцию Хэвисайда? Потому что любое изменение цены в момент времени t1 на величину m можно описать как прибавление в момент времени t1 к предыдущему значению цены функции Хэвисайда с весом m. А весь график цены во времени представляет собой не что иное, как сумму множества функций Хэвисайда, соответствующих отдельным тикам графика с весами и знаками приращений цены по этим тикам. Записывать выражение для суммы лень, много суеты по клавиатуре.
Вследствие принципа суперпозиции спектр графика такого цены будет представлять собой бесконечную сумму гиперболических функций ~1/j2пf с разными весами и различным фазовым сдвигом, определяемым временем тика. И тут мы приехали… Мы всегда будем иметь дело с откликом на прошлые значения цены, но этот отклик никоим образом не влияет ни на величину ни на знак, ни на моменты прибавления новых функций Хэвисайда, соответствующих будущим тикам графика.
Если бы график цен был периодическим или хотя бы квазипериодическим, то преобразование Фурье можно было бы заменить рядами Фурье, что дало бы возможность худо-бедно прогнозировать будущее движение цены. Но чего нет того нет… Поэтому про Фурье и гармонический анализ забываем раз и навсегда.
Читайте на SMART-LAB:
X5 проведёт вебкаст по результатам 2025 года
Друзья, всем привет! Рады пригласить вас на вебкаст, посвящённый финансовым результатам X5 за 2025 год. В ходе звонка мы подведём итоги 2025 года, расскажем о рыночных тенденциях и прогрессе Х5 в...
16:13

🔒 Что скрывает под собой доходность
Как узнать, какой актив показал себя успешнее на дистанции? Сравнить их исторические доходности. Но у этого показателя есть два существенных ограничения: 🔵Прошлая доходность не гарантирует...
15:34











Люди забывают, что математика — это инструмент описания отношений, а не инструмент моделирования динамических систем реального мира, она тут плохо подходит, в силу своей декларативной природы