То ли робот, то ли нет

Не то, чтобы дарю грааль.
На рынке всё хорошо.
Поэтому немного исследований почти сферического коня почти в вакууме.

Смысл топика скорее в том, чтобы показать, какого типа память присуща биржевым данным и какой может быть торговая система, основанная на такой памяти.

Исходные данные — обычные часовые бары по акциям Сбербанка, для которых строится средняя цена.

Подход:
1. Рассматриваем группы часовых баров по 9 штук, отражающих скользящий день. 
2. Предполагаем, что группы баров, кончающихся в одни и те же часы, в среднем должны быть похожи.
3. Выбираем глубину предыстории (2-3-4 месяца), в которой будем находить похожие вектора.
4. Для данного текущего вектора находим в прошлом похожие вектора (скажем 10-15 штук), для которых мы знаем, каким был следующий часовой бар. По ним делаем оценку (можно среднее, можно авторегрессию, можно всё, что угодно) следующего бара для нашего текущего.
5. Принимаем решение о входе (не-входе) в ту или иную позицию на один час.

Получаются следующие торговые результаты за 7 лет:































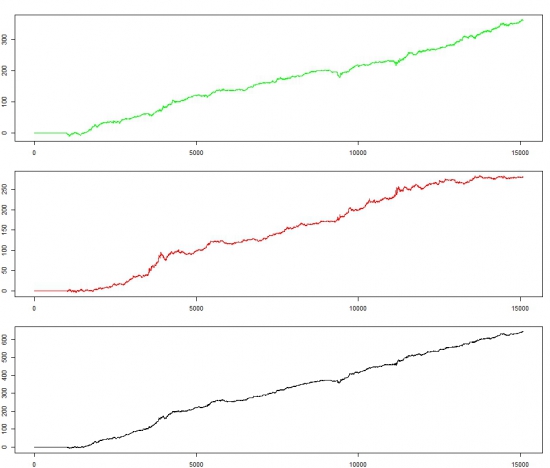
Абсцисса это доход в процентах. Ордината это порядковый номер часа. Эквити почасовые:
зеленая — лонги,
красная — шорты,
черная — лонги+шорты.

Расчеты сделаны исходя из идеальных условий:
1. Входим по open следующего бара без проскальзывания по рынку.
2. Выходим по close следующего бара без проскальзывания по рынку.

Общая средняя сделка равна 0.046%.
По лонгам средняя сделка равна 0.053%.
По шортам средняя сделка равна 0.039%.
Лонги заняли 46% баров.
Шорты заняли 51% баров.

В приведенных результатах показан оптимальный случай исходя из перебора глубины, в которой ищем похожие вектора (от 1 до 6 месяцев), а также количество ближайших векторов к текущему (от 1 до 50). В худших случаях результаты примерно в два раза хуже приведенных.