Модель скрытых состояний Маркова. Часть 1
В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R. Вначале будет много теории, ее надо хотя бы попробовать понять, затем разберем практические примеры.
Рабочая среда распознавания основных паттернов.
Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:
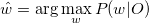
Так как P(w|O) неизвестен, применяем правило Байеса:
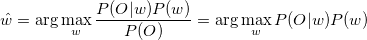
Максимизация не зависит от P(O), поэтому мы можем игнорировать эту вероятность. P(O|w),P(w) означают вероятность того, что данные O принадлежат классу w и вероятность существования класса w соответственно.P(O|w) определяется моделью скрытых состояний Маркова.
Формулировка задачи.
Сначала нам нужно сгенерировать набор признаков О из рыночных данных d. Пока пропустим этот шаг, потому что он будет различаться для разных применений модели Маркова, например для финансов d может быть представлен ценами разных активов и О можно обозначить набор технических индикаторов, применяемых к d. Модель Маркова также популярна в задачах распознавания речи, где О обычно является вектором, описывающим характеристики частотного спектра речи.
Затем необходимо вектор О ассоциировать с классом модели Маркова. Это можно сделать путем применения метода максимального правдоподобия, где модель Маркова определяет класс, который с наибольшей вероятностью генерирует набор параметров, соответствующий набору параметров О.
Спецификация модели Маркова.
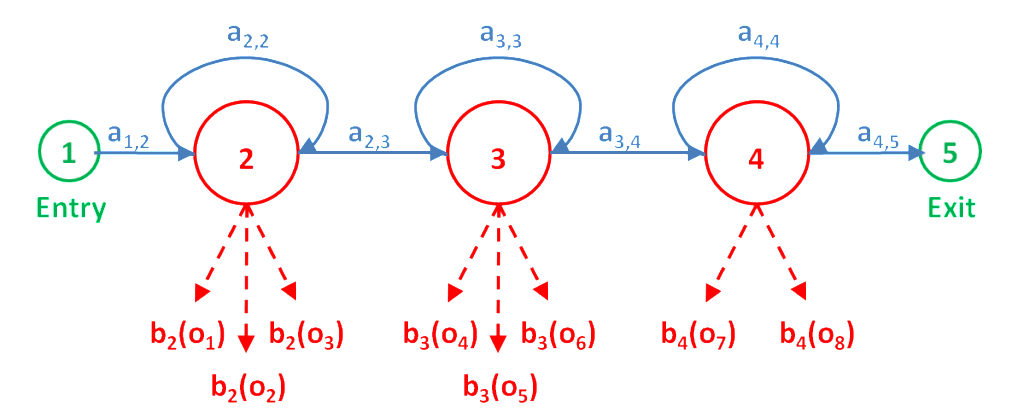
Рассмотрим рисунок в заглавии поста. На нем приведены следующие обозначения:
N — число состояний модели (на рисунке равно 5),
ai,j- вероятности перехода из состояния i в состояние j,
bj(O)- вероятность получения вектора параметров О при состоянии j ( j не является входным и выходным состоянием),
вектор параметров модели Маркова λ определим как ![Модель скрытых состояний Маркова. Часть 1 \lambda=[N,a_{i,j},b_j]](http://mathurl.com/mtqzz2r.png) ,
,
![Модель скрытых состояний Маркова. Часть 1 O=[o_1,o_2,...,o_T]](http://mathurl.com/k4skrbw.png) — вектор параметров наблюдений,
— вектор параметров наблюдений,
![Модель скрытых состояний Маркова. Часть 1 X=[x_1,x_2,..,x_T]](http://mathurl.com/lt7m9qs.png) — найденный вектор последовательности состояний.
— найденный вектор последовательности состояний.
Совместная вероятность соответствия вектора О последовательности состояний X при параметрах модели λ равна вероятности перехода из текущего состояния в следующее, умноженное на вектор параметров, сгенерированный в этом состоянии:
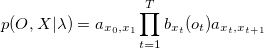
где x0,xT+1- входное состояние 1 и выходное соcтояние N соответственно.
Вычисление вероятности.
В рассмотренной выше совместной вероятности мы определили последовательность состояний X. Так как эта последовательность является скрытой переменной ( вот почему модель Маркова называется моделью скрытых состояний), мы ее не знаем. Однако, если мы суммируем вероятности по всем возможным состояниям, то получим:
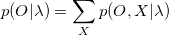
Это может быть проблематичным из-за большого числа состояний модели (особенно в приложениях реального времени), но существуют эффективные алгоритмы для такого вычисления, без нахождения каждого отдельного состояния. Подобным алгоритмом является форвардный алгоритм.
Что представляет из себя bj(o)?
Это полученное распределение вероятностей при состоянии j модели. Это распределение может быть любым, но оно должно соответствовать распределению данных при состоянии j, и должно быть математически определяемым. Обычным выбором на этой стадии является предположение, что вектор O может описываться набором гауссовских распределений — мультивариантным нормальным распределением. В качестве предупреждения отметим, что если составляющие вектора параметров сильно коррелированы между собой, тогда Σ- ковариационная матрица — будет иметь много вычисляемых значений. В этом случае нужно подбирать вектор парметров так, чтобы Σ представляла собой диагональную матрицу, другими словами, параметры не должны быть кореллированы между собой:
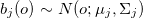 , где μ,Σ- параметры мультивариантного гауссовского распределения.
, где μ,Σ- параметры мультивариантного гауссовского распределения.
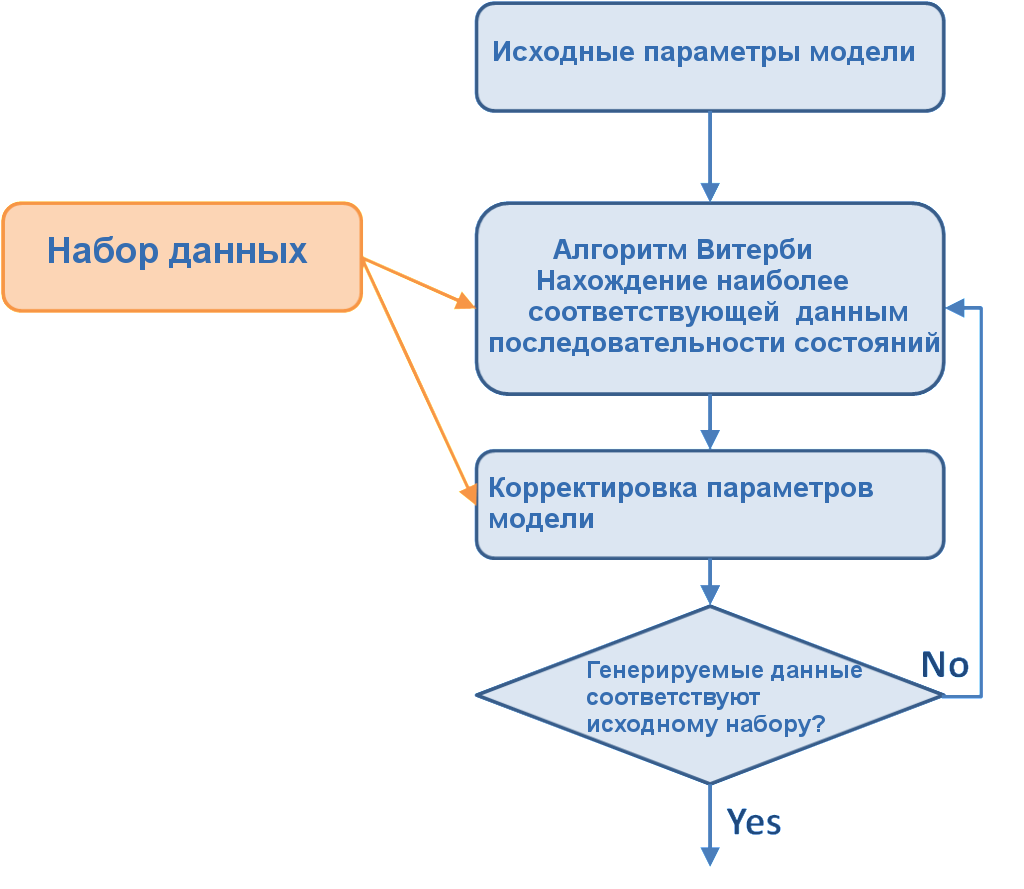
Как получить bj(o)? Определение параметров методом Витерби.
Мы знаем, что для описания нормального распределения достаточно методом максимального правдоподобия вычислить среднее распределения μ и ковариацию Σ вектора параметров. Значит мы должны получить только среднее и ковариацию вектора параметров для состояния j нашей модели, используя так называемую сегментацию Витерби. Она подразумевает нахождения жесткого соответствия между вектором параметров и последовательностью состояний, которое его генерировало. Существует также и альтернативный метод Баума-Вельша, который ассоциирует вектор параметров с несколькими последовательностями состояний с определенной вероятностью.
Состояние j генерирует наблюдения, начиная с tj:
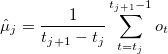
![Модель скрытых состояний Маркова. Часть 1 \hat{\Sigma}_j=\frac{1}{t_{j+1}-t_j}\sum_{t=t_j}^{t_{j+1}-1}[(o_t-\hat{\mu}_j)(o_t-\hat{\mu}_j)^{`}]](http://mathurl.com/phl9ofv.png)
Наперед неизвестно, какая последовательность какой вектор наблюдений генерирует, но существует алгоритм Витерби, позволяющий решить эту проблему с некоторым приближением:
Подробно алгоритм Витерби, а также форвардный алгоритм для эффективного вычисления p(O|λ) рассмотрим в следующей части.
Другие стратегии, применяемые в алгоритмической торговле и биржевых роботах смотрите в моем блоге и на сайте.
 Алексей 88812 мая 2015, 14:47Спасибо. Интересно0
Алексей 88812 мая 2015, 14:47Спасибо. Интересно0 Мимо проходил12 мая 2015, 14:56Я восхищен! Наверное вы очень богаты :)+8
Мимо проходил12 мая 2015, 14:56Я восхищен! Наверное вы очень богаты :)+8 SergeyJu12 мая 2015, 14:58Какой содержательный смысл можно, на Ваш взгляд, вложить в различные состояния, включая состояние EXIT?0
SergeyJu12 мая 2015, 14:58Какой содержательный смысл можно, на Ваш взгляд, вложить в различные состояния, включая состояние EXIT?0