Алгоритмы маркетмейкера. Часть 3
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ, как достижение максимума следующего матожидания:
![Алгоритмы маркетмейкера. Часть 3 \max_{\theta^{mk},\theta^{tk}}\mathbb{E}_0[X_T-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/pthr6jr.png) ,
,
где интеграл![Алгоритмы маркетмейкера. Часть 3 \gamma\int^T_0 Y^2_{t-}d[P,P]_t](http://mathurl.com/ptd6xfu.png) представляет собой штрафную функцию удержания ненулевой открытой позиции рискованного актива, γ- постоянный коэффициент, d[P,P]t- квадратичное изменение средней цены P,
представляет собой штрафную функцию удержания ненулевой открытой позиции рискованного актива, γ- постоянный коэффициент, d[P,P]t- квадратичное изменение средней цены P, 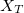 — кэш трейдера на момент времени окончания торговли T.
— кэш трейдера на момент времени окончания торговли T.
Далее определим функцию, которая представляет активы трейдера после ликвидации всех открытых позиций в конце торговли по алгоритму с помощью маркет ордера:
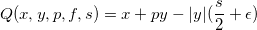 ,
,
где x — кэш трейдера,
p- средняя цена (в стакане),
y — открытая позиция,
s — спред,
f — дисбаланс объемов в стакане,
ϵ- комиссия.
С учетом функции Q дадим определение так называемой функции владения, которую мы и будем максимизировать на всем протяжении работы алгоритма:
![Алгоритмы маркетмейкера. Часть 3 V(t,x,y,p,f,s)=\sup_{\theta^{mk},\theta^{tk}}\mathbb{E}_t[X_T+P_T Y_T-|Y_T|(\frac{S_T}{2}+\epsilon)-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/monr2f5.png)
Проблема оптимального контроля решается с применением динамически программируемых уравнений, и для составления первого уравнения для котировочных стратегий θmk представим инфинитезимальный оператор второго порядка L:
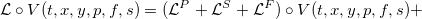
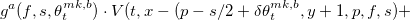
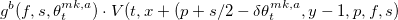
 — инфинитезимальные операторы процесса изменения средней цены P, дисбаланса объема в стакане F и спреда S соответственно. Несмотря на страшное название данные операторы просто обозначают воздействие изменяющихся в течение времени процессов цены, дисбаланса объема и спреда на функцию владения — то есть на активы, которыми владеет трейдер. Функции
— инфинитезимальные операторы процесса изменения средней цены P, дисбаланса объема в стакане F и спреда S соответственно. Несмотря на страшное название данные операторы просто обозначают воздействие изменяющихся в течение времени процессов цены, дисбаланса объема и спреда на функцию владения — то есть на активы, которыми владеет трейдер. Функции
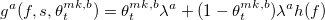
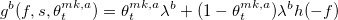
являются ни чем иным, как ожидаемой частотой исполнения лимитных ордеров на биде и аске соответственно. Здесь h(f)- вероятность взятия лимит ордера на лучшем аске(биде) в очереди заявок, в зависимости от дисбаланса f, имеет форму 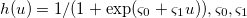 — положительные константы.
— положительные константы. 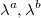 — частоты прихода маркет ордеров на бид и аск.
— частоты прихода маркет ордеров на бид и аск.
Для составления вторoго уравнения стратегии с маркет ордерами (take strategy) θtk , нам понадобится оператор импульсного управления M:
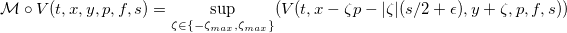
Этот оператор отражает воздействие на функцию V(t,x,y,p,f,s) стратегии θtk, с целью максимизации функции владения во время применения этой стратегии.
С операторами L и M мы сможем составить неравенство, которое называется квазивариационное неравенство Хамильтона-Якоби-Беллмана (HJB-QVI):
![Алгоритмы маркетмейкера. Часть 3 \max\left\{\frac{\partial V}{\partial t}+\sup\{\mathcal{L}\circ V\}-\gamma y^2\frac{\mathbb{E}_t[P,P]_t}{dt},\mathcal{M}\circ V-V\right\}=0](http://mathurl.com/ou32lqc.png) , на промежутке[0,T), (T- время ликвидации открытых позиций (окончание торговли)), и составляет систему уравнений с терминальным условием:
, на промежутке[0,T), (T- время ликвидации открытых позиций (окончание торговли)), и составляет систему уравнений с терминальным условием:
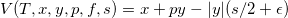
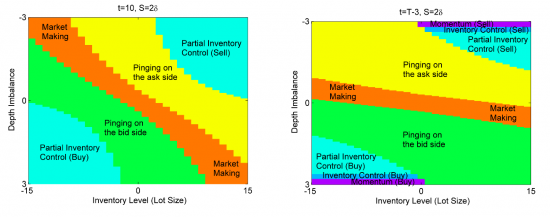
Решением этой системы уравнений и будет набор стратегий θmk ,θtk, вычисленные на каждый момент времени в промежутке [0,T), и на каждую величину спреда s, как изображено на графиках в заглавии статьи. Обратите внимание, что там появилась новая область в связи с размером спреда S больше одного шага цены — Pinging on bid\ask side. В этой области значения θmk равны 1 для бида/аска, что означает, что лимитные ордера выставляются в стакане на тик больше бида (тик меньше аска) — см. часть 2 цикла статей.
В следующей части рассмотрим как решить систему уравнений численными методами. Продолжение смотрите на моем сайте (см. профиль) или через некоторое время на смарт-лабе. Прошлые части статьи — в моем блоге.














Умников здесь не любят, до и понторезов тоже)))