Направленная торговля опционами
Предлагаю обсудить одну идею направленной торговли опционами. Прочитал о ней в книге «Опционы. Системный подход к инвестициям. С. Израилевич, В. Цудикман» (спасибо Стасу за наводку) и загорелся попробовать. Слегка доработал, частично реализовал и хотел бы поделиться промежуточными результатами. Буду рад любой критике, новым идеям и т.д.
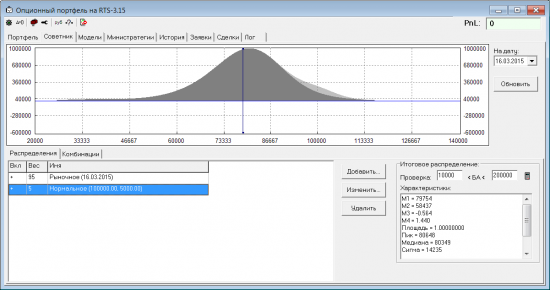
Суть идеи в том, чтобы по распределению вероятностей оценивать различные опционные позиции и выбирать лучшие из них. Для иллюстрации рассмотрим позицию «голый фьючерс» на основе рыночного распределения:
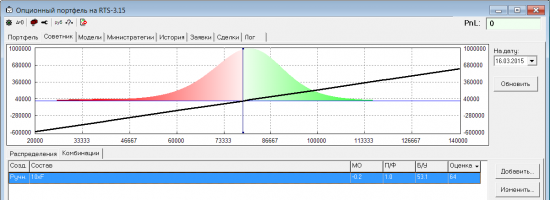
Вот какие показатели можно рассчитать по распределению:
- Матожидание PnL (МО) — среднее PnL всех возможных исходов считается как интеграл произведения платежной ф-ции на экспу на функцию плотности распределения. Чтобы можно было сравнивать этот показатель у различных комбинаций разного объема, решил нормировать его на общий риск позиции. Для простоты и скорости вычисления в качестве меры риска взял не ГО, а VaR.
- Вероятность безубытка (Б/У) — площадь под теми участками распределения, где платежная ф-ция не отрицательна (т.е. площадь зеленых участков распределения).
- Профит-фактор (П/Ф) — считается как отношение матожидания прибыли к матожиданию убытка (отдельно считается матожидание на зеленых участках и отдельно на красных).
Для рассматриваемого примера матожидание PnL получилось почти 0 (0.002%, не чистый ноль из-за погрешности вычислений), и профит-фактор = 1. Т.е. средняя прибыль будет равна среднему убытку. И так получается для любой опционной позиции, открытой по теорценам. Т.е. если использовать только рыночное распределение, не получится выявлять комбинации с положительным матожиданием и профит-фактором > 1.
Под рыночным распределением понимаю распределение, построенное по лучшим бид-аскам из опционных стаканов. Т.е. если посчитать по нему справедливые цены, то они будут между текущими бид-асками во всех стаканах (на всех страйках данной календарной серии). Если не ошибаюсь, такое распределение называется рискнейтральным, и его первый момент равен текущему значению фьючерса.
Поэтому, если мы собираемся торговать направленно, одним только рискнейтральным рыночным распределением не обойтись. В соответствии со своим прогнозом, можно добавить к нему с определенным весом нормальное, или логнормальное, или вообще равномерное (если считаем, что на экспу БА будет в определенном диапазоне с равной вероятностью). В упомянутой книжке было предложение добавлять еще эмпирическое распределение (если верим в то, что история приращений будет повторяться). Еще, случайно обнаружил в книге «Математика управления капиталом. Ральф Винс» формулу для произвольного распределения, где четыре параметра регулируют первые четыре момента распределения. С помощью смеси таких распределений можно получать самые причудливые формы:
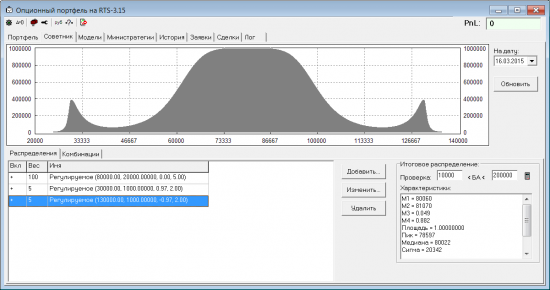
Т.е. если есть собственный взгляд (отличающийся от рыночного) о вероятности, где будет БА на экспу, то технических проблем подобрать соответствующее распределение — нет. Ну а если собственного вью нет, то и направленную позу лучше не открывать, и торговать только дельтанейтральные стратегии.
Допустим, мы предполагаем рост и уверены в своем прогнозе на 5%. Составляем смесь распределений: рыночное с весом 95% и соответствующее нормальное с весом 5%:
Получаем небольшую припухлость на правом хвосте распределения. Распределение перестало быть рискнейтральным, и появился смысл искать на нем комбинации с положительным МО. Чтобы иметь возможность сравнивать между собой различные комбинации, сведем все вычисляемые показатели в одно число. Для этого назначаем каждому показателю свой вес (в зависимости от того, что нам важнее — возможная прибыль или безрисковость) и делаем «аддитивную свертку». Для примера взял такие веса: 0.4/0.3/0.3. Т.е. итоговая оценка вычисляется примерно так: 0.4*МО + 0.3*П/Ф + 0.3*Б/У. Сравним теперь между собой несколько стандартных комбинаций, направленных на рост:
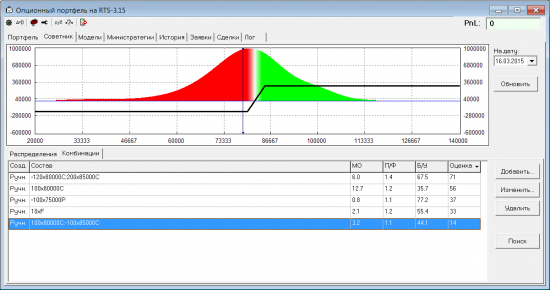
Самая слабенькая оценка у бычьего колл спрэда. Небольшое положительное МО, П/Ф чуть больше 1, и маленькая вероятность выйти в безубыток. Итоговая оценка 14.
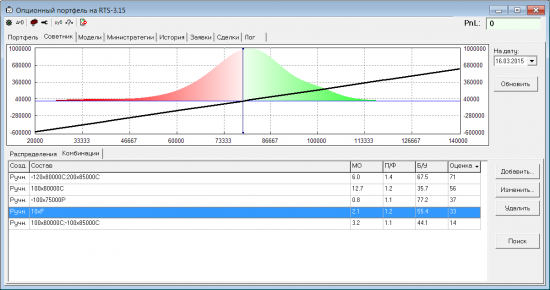
Голая покупка фьюча неожиданно оказалась лучше бычьего спрэда. Думал, что эта поза будет на последнем месте.
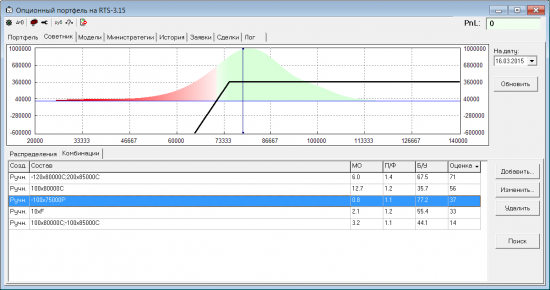
Чуть лучше показатели у проданного пута. У позиции самая большая вероятность выйти в Б/У. Но самое маленькое МО.
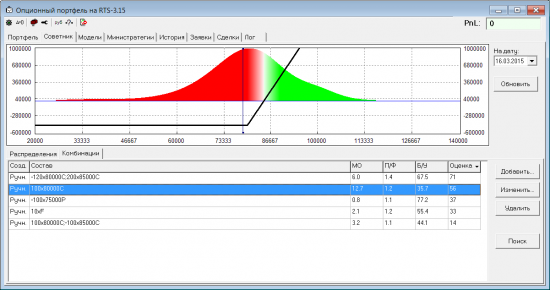
На втором месте — покупка колла. Самое большое МО, но и самая маленькая вероятность выйти в Б/У.
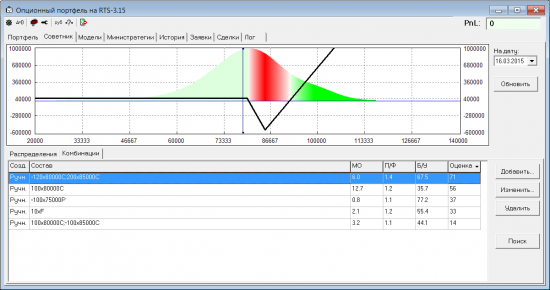
Победителем, с хорошим отрывом по очкам, оказался пропорциональный колл спрэд. У него все показатели хорошие, итоговая оценка 71.
Вот такие результаты получились. Может, кто из практиков направленной торговли выскажется — соответствуют ли такие результаты опыту торговли?
Собираюсь теперь прикрутить автоматический поиск комбинаций с помощью геналгоритмов. Если это получится, то можно будет применять его не только для поиска наилучшей для открытия позы, но и для управления уже открытой позы. Допустим, раз в два-три дня пересматривать распределение вероятности (как минимум, будет меняться рыночное, а может и собственный прогноз изменится). И потом по новому распределению искать, как с помощью минимальных изменений в позиции улучшить ее показатели. Получается такая неторопливая стратегическая торговля, где прогнозируешь не очередное приращение цены, а вероятность того или иного возможного сценария. Нет тейкпрофитов (когда борешься с жадностью), проблемы выбивания стопов и внутренней борьбы «а не отодвинуть ли еще немного стоп». И не будет соблазна на какой-нибудь совсем плохой вариант, типа усреднения убыточной позиции. Анализ по распределению четко покажет, что это будет ухудшением позы.
Но есть и некоторые сомнения — может, это все пустое и не более чем красивые картинки. Все-таки тут слишком много степеней свободы: веса для оценок, распределение — одна сплошная неопределенность. И вероятностный анализ работает все-таки при большом кол-ве попыток. Положительное матожидание PnL совсем не гарантирует от убытка в отдельном трейде.
В общем, было бы интересно узнать — у кого какое мнение по поводу такого подхода к торговле?
по поводу скоринга (свёрток мо, п/ф итд) — это тоже вариант, но есть более менее устоявшееся «мерило», и возможно оно вам понравится (например, его можно подифференцировать и получить желаемое без ген алгоритмов) — функция полезности
я использую самую банальную, логарифмическую.
скажем имеются средства M и опционная конструкция, которая имеет функцию выплат P(F, T)
на этом этапе вовсе не обязательно, чтобы M как-то предварительно соотносилось с функцией выплат или премией полученной/затраченной на конструкцию
рассмотрим величину U(F, T) = ln((M + P) / M) = ln(1 + R)
если масштаб R позволяет разложить U по тейлору — то:
для первого порядка получим: M(U) = M( R ) — т.е. матожидание полезности это матожидание прироста средств в %, где матожидание вычисляется по _не_рискнейтральной мере (а именно по той, относительнго которой оптимизируете конструкцию)
для второго порядка: M(U) = M( R ) — 0.5 * M(R^2) — здесь уже учитывается рисковость позиции
для третьего: M(U) = M( R ) — 0.5 * M(R^2) + 1/3 * M(R^3) — вклад ассиметрии
ну и так далее… окончательно — можно интерпритировать M(U=ln(1+R)) как некоторый скоринг, учитывающий все моменты процентного прироста средств R в _не_рискнейтральной мере
и относительно этого скоринга находить оптимальную позицию для заданной пары {рискнейтральная мера, нерискнейтральная мера}
спасибо, очень интересно! Правильно ли понял, что могу посчитать M(U) (скажем до 4го порядка) для каждой комбинации (опционной позиции) и наибольшее значение будет соответствовать самой лучшей комбинации?
Если на данном этапе не важно соотношение начальных средств и рассматриваемой комбинации, то можно взять M=1, и R будет равно P?
Насчет последней фразы — предлагаете искать оптимальную позу не только по смешанному распределению, но и по рыночному? А какой в этом смысл, если я уже использовал рыночное распределение, взяв его с некоторым весом в смесь?
Или имеете ввиду, что можно попытаться найти такую комбинацию, которая имела бы хорошие показатели на нерискнейтральном распределении, и при этом была дельтанейтральной на рыночном распределении? Т.е. если собственное вью на экспу окажется верным, то получим прибыль, а если нет, то — только накладные расходы на поддержание дельтанейтральности?
> Правильно ли понял, что могу посчитать M(U)
> (скажем до 4го порядка) для каждой комбинации
> (опционной позиции) и наибольшее значение будет
> соответствовать самой лучшей комбинации?
про моменты — пример был чтобы показать, что матожидание логарифмической полезности «это тоже вобщем-то скоринг» (возможно стоило написать, что т.к. любой персентиль есть функция моментов, то и вероятность безубытка, и профит-фактор — тоже функции моментов)
переформулирую свою мысль: матожидание полезности лучше считать как именно M(ln(1+R)), не обрывая ряды Тейлора, они тут были просто иллюстрацией того, что представляет из себя матожидание логарифма случайной величины.
смешанное распределение (рынок + вью) — это тоже уже не рынок, а вью, поэтому чтобы не путаться, будем называть рыночное распределение (из улыбки) рискнейтральным Q, а какое-то наше — нерискнейтральным P
обычно задача ставится так: рынок, находится в состояние предполагающем распределение Q, участник заключает, что цена актива имеет распределение P. участник располагает средствами M (да, можно считать что равными 1). вопрос — какую «лучше» сформировать позицию? ответ — найти такую позицию, которая максимизирует ожидаемую полезность M(ln(1+R)) относительно распределения P.
> Насчет последней фразы — предлагаете искать
> оптимальную позу не только по смешанному
> распределению, но и по рыночному? А какой
> в этом смысл, если я уже использовал рыночное
> распределение, взяв его с некоторым весом в смесь?
{рискнейтральная мера (Q), нерискнейтральная мера (P)} — вы про это место? имелось ввиду вот что: от Q зависит платёжная функция, проще говоря, при некотором Q цена стредла это 100 рублей, а при каком-то другом Q это 1000 рублей, от вью P цены не зависят (покрайней мере пока вы не открыли позицию) соответственно при разных Q этот стредл может быть интересен как в покупку так и в продажу, т.е. оптимальная позиция — это функция не только от вью P (пусть даже оно учитывает Q), но и от рынка Q непосредственно. матожидание полезности при этом вычисляется именно по мере P.
> Или имеете ввиду, что можно попытаться найти
> такую комбинацию, которая имела бы хорошие
> показатели на нерискнейтральном распределении,
> и при этом была дельтанейтральной на рыночном
> распределении?
идея интересная, но всё проще — см выше
О, теперь многое прояснилось, большое спасибо!
Попробую оценить через матожидание полезности. Напишу какой будет результат и отличие от оценки через «свертку». Только, про средства М=1 — наверное, это я погорячился. Тогда ведь ln(1+R) на убыточных участках будет не посчитать. Видимо нужно взять М чуть больше, чем максимальный убыток (минимальное значение ф-ции выплат) на всем диапазоне, где у меня задано распределение.
это не проблема, вы как нулевое приближение возьмите веса 0 для всех страйков (и фьюча), а далее градиентным спуском, если взять M=1, то на выходе получатся какие-то небольшие веса, для других M они просто будут пропорционально больше
с чем можно столкнуться:
1. оптимизация помимо того что должна делать надувает нейтральные позиции, типа: «добавилось колов, что-то ещё, убавилось путов, что-то ещё, убавилось фьюча», т.е. с каждой итерацией в портфеле набирается ничего не значащаяе компонента с общим страйком N*(+call-put-futures) — в этом случае стоит либо «прочищать» портфель вконце итерации, либо исключить путы — они линейнозависимы с колом и фьючерсом и сами собой окажутся синтетически реализованы если они нужны
2. если плохо сходится — выкиньте половину страйков (например каждый второй), оптимизируйте, добавте выкинутые, переоптимизируйте
3. не ожидайте на выходе понятную позицию, войдёт весь спектр того что было на входе
это уже про поиск оптимальной позы? Пока хотелось бы научиться правильно оценивать фиксированный список вручную заданных комбинаций.
Добавил подсчет матожидания полезности. В некоторых случаях получились кардинально другие оценки по сравнению со «сверткой». Вот пример. Старый метод показывает, что самая лучшая поза купленный колл. А M(ln(1+R)) выдает самое маленькое значение для этой позы (-1.66).
В расчетах брал средства (лучше ее S обозначить, а не M, чтобы не путать с символом матожидания) как S=1.01*Abs(MaxLoss). Т.е. считал M(U)=M(ln(1 + (P/S))).
Получается что MaxLoss у купленного колла небольшой, а у проданного пута — на порядок больше. Возможно, поэтому оценка (через матожидание полезности) у купленного колла оказалась на два порядка хуже проданного пута. Из общих соображений, старый метод расставил оценки более правильно, имхо.
> Старый метод показывает, что самая лучшая поза
> купленный колл. А M(ln(1+R)) выдает самое маленькое
> значение для этой позы (-1.66).
всё правильно, это оттого что S=1.01*Abs(MaxLoss) чуть больше худшего убытка, поэтому с вероятностью почти Б/У (почти 60%) вы получаете очень отрицательный логарифм.
выбор S существенен, в данном случае вы оцениваете полезность игры: лосс ~99% с вероятностью ~60% и прибыль с вероятностью ~40%
теория полезности строится исходя из того, что S задаётся честно, то есть если рассматривается сценарий убытка на 99% S, то это действительно убыток на 99% средств участника (у участника нет средств кроме S)
что касается скоринга — если на входе позиция с уже заданными весами, то тогда следует провести оптимизацию по S, и найти сам максимум и S, при котором он достигается
наверное, чтобы сильно не ломать голову, но почувствовать полезность, проще добавить в таблицу 4 (мб больше) столбца с полезностями посчитанными для разных S:
S1 = 1.01*Abs(MaxLoss)
S2 = 1.1*Abs(MaxLoss)
S3 = 2*Abs(MaxLoss)
S4 = 11*Abs(MaxLoss)
> Получается что MaxLoss у купленного колла небольшой,
> а у проданного пута — на порядок больше. Возможно,
> поэтому оценка (через матожидание полезности)
> у купленного колла оказалась на два порядка хуже
> проданного пута. Из общих соображений, старый
> метод расставил оценки более правильно, имхо.
да, причина в этом, не уверен что из этого получится, но как вариант — если найти самый большой GlobalMaxLoss по всему списку (и по колам и по путам, всё что есть в таблице) и посчитать ожидаемую полезность относительно GlobalS=1.01*Abs(GlobalMaxLoss), или вовсе завести ManualS и задать его руками, то ожидаемая полезность подтянется к интуитивно понятным цифрам
Ах вот в чем дело, теперь понятно! Действительно большая зависимость от S, вот что получилось. При S4 расстановка оценок — почти такая же как у свертки.
(S5 = 1.01*Abs(MaxPnL). Добавил еще три комбинации направленных на падение, чтобы убедиться что они оцениваются хуже всего.)
Получается, нужно искать не только оптимальную позу, но еще и оптимальную S для каждой позиции-кандидата?
Насчет GlobalMaxLoss, тоже подумал. Но тогда получится абсолютное сравнение позиций, а хотелось бы их сравнивать в нормированном состоянии. Т.е. хотелось бы, чтобы позы «10*Fut» и «1000*Fut» показывали одинаковую оценку. Масштабировать найденную оптимальную позу к реальным деньгам — это уже следующая задача.
P.S. А можно сказать что матожидание полезности — это матожидание доходности (где доходность считается к использованному S)?
с S5 не совсем понял — это Abs(MaxPnL) это по сути MaxProfit или Max(Abs(PnL))?
> Получается, нужно искать не только
> оптимальную позу, но еще и оптимальную
> S для каждой позиции-кандидата?
> хотелось бы их сравнивать в нормированном
> состоянии. Т.е. хотелось бы, чтобы позы «10*Fut»
> и «1000*Fut» показывали одинаковую оценку.
> Масштабировать найденную оптимальную позу к
> реальным деньгам — это уже следующая задача.
да, верно, просто исторически задача ставилась с противоположной стороны :) то есть: «что лучше сделать участнику с средствами S, если рынок предполагает Q, а участник предполагает P». в вашей постановке достаточно для каждой строки найти S максимизирующее ожидаемую полезность, при оптимальном S для 10*Fut и 1000*Fut полезность окажется одинаковой.
И ещё пару слов о нормированности — суть полезности, отчасти и в том, что она улавливает, что при депозите 100 рублей например 5 коллов это хорошо, а 6 или 4 — хуже.
Да, имел ввиду Max(Abs(PnL)).
Сделал чтобы для каждой позы можно было посмотреть график, как изменяется матожидания полезности (может его MOP обозначить?) в зависимости от SM: S = SM*Abs(MaxLoss). Вот какой график получился для лонг колл. Правильный ли вывод делаю из этой картинки: на данном распределении максимальная ожидаемая доходность будет +2.8%, при условии что покупается такое кол-во коллов, которое выдает максимальный убыток в 6-7 раз меньше выделенных денег на портфель?
Вот еще какие графики выдает:
1. Для лонг фьюч (у проданного пута примерно такая же), т.е. здесь максимум MOP будет достигаться при минимально возможной S.
2. Для комбинаций с отрицательным матожиданием PnL (например, шорт фьюча или лонг пут на распределении с заложенным ростом) получаются вот такие графики. Т.е. можно считать сначала просто матожидание PnL, и если оно отрицательное, то и не пытаться искать оптимальное S, а сразу браковать комбинацию.
Похоже на правду?
> Правильный ли вывод делаю из этой картинки: на данном
> распределении максимальная ожидаемая доходность будет
> +2.8%, при условии что покупается такое кол-во коллов,
> которое выдает максимальный убыток в 6-7 раз меньше
> выделенных денег на портфель?
про 6-7 раз — да, правильный, про +2.8% — в первом порядке да, но вобще говоря больше, так как MU = Mln(1+R) <= MR
> 2. Для комбинаций с отрицательным матожиданием
> PnL (например, шорт фьюча или лонг пут на
> распределении с заложенным ростом) получаются вот
> такие графики. Т.е. можно считать сначала просто
> матожидание PnL, и если оно отрицательное, то и
> не пытаться искать оптимальное S, а сразу браковать
> комбинацию.
да, собственно это как раз из MU = Mln(1+R) <= MR следует
> Похоже на правду?
вроде похоже, на всякий случай добавлю в классической постановке оптимальная позиция имеет неотрицательную полезность, т.к. всегда есть вариант «отсутствие позиции» который имеет MOP = 0
Стал читать Ральфа Винса, где он рассуждает про оптимальную f (оптимальная доля счета для торговли), и решил немного переиначить постановку. Пусть S*F = MaxLoss, где S — деньги на позицию, MaxLoss — максимальный убыток позиции, F — доля денег на позицию. Задача — найти максимум матожидания полезности (МОП). Тот F, при котором будет достигаться этот максимум, назовем оптимальное F.
Сделал поиск такого максимума на фиксированном списке комбинаций и вот какие результаты получились. Для ситуации, когда анализируем только на рыночном распределении (P = Q), результат такой: макс МОП для всех комбинаций равен 0. Т.е. как бы мы не регулировали F — положительную полезность на рискнейтральном распределении не получить (а отрицательную с помощью неправильного F — легко).
Для ситуации P = Q + рост, результат такой: наибольший МОП у лонг колла и оптимальное F = 0.25. Т.е. если такой колл стоит 1000, у нас денег 8000, то нужно купить 2 колла. По полезности лонг колла обогнал лонг фьюча в 4 раза. При этом для фьюча нужно было открываться «на все».
Интересно, что график зависимости МОП от F у лонг фьюча — непрерывно растет и не имеет выраженного пика. А у опционных позиций — пик есть.
Кстати, для последнего распределения ранжирование через свертку и через МОП — полностью совпало.
> Интересно, что график зависимости МОП от F у лонг
> фьюча — непрерывно растет и не имеет выраженного
> пика. А у опционных позиций — пик есть.
мне кажется это потому, что у вас распределение P изначально «квазиарбитражное», т.е. M(PnL) > (D(PnL))^0.5 (для фьючерсной позиции по мере P)
объяснить ситуацию наглядно, но не аккуратно, можно так: дискретное приближение стохастического процесса это Fut(T) = Fut(0) + \myu T + \sigma * T^0.5 * \epsilon, где \epsilon ~ N(0, 1), PnL(T) = pos * (Fut(T) — Fut(0))
теперь положим T = 1, и рассмотрим два случая \epsilon = {-1, 1}, в обоих этих случаях позиция лонг фьючерса даст положительный результат (так как \myu > \sigma), т.е. в такой урезаной моделе риска как бы совсем нет
в полновесной моделе с интегрированием логарифма по всей оси происходит качественно то же самое
почему для колов есть пик? потому, что там есть расход — платится премия (тут существенна только временнАя компонента премии), можно ещё страйк колла устремить к 0 (то есть устремить колл к фьючерсу), и посмотреть динамику оптимального F в зависимости от страйка, то предположительно (никогда этого не делал) для квазиарбитражного распределения она будет чем-то отличаться от динамики не квазиарбитражного распределения
проще говоря — в P = Q + рост — подвиньте рост поближе к рынку и/или поднимите его дисперсию и/или понизьте его вес и должен появиться пик на фьючерсе
> Кстати, для последнего распределения ранжирование
> через свертку и через МОП — полностью совпало.
не получается воспроизвести столбец свертка через другие столбцы и веса 0.4/0.3/0.3, напишите подробнее, как вы её считаете? это Ваша разработка или где-то можно почитать?
Для свертки использую не абсолютные оценки, а перевожу их в доли, и только потом умножаю на веса и складываю. Вначале вычислял возможные диапазоны динамически, пробегался по всем комбинациям и брал min/max значения оценок. Т.е. суммировал такое: вес*(оценка — min)/(max-min).
Но потом решил переделать (не понравилось что итоговая оценка любой комбинации зависит от наличия других комбинаций), и сделал диапазоны фиксированными:
МО: Min=0, Max=10
П/Ф: Min=1, Max=10
Б/У: Min=0, Max=100
Теперь, наверное, вообще уберу оценку через свертку. Ваш вариант через полезность мне нравится гораздо больше: не нужны веса и сразу готов ответ про объем позиции.
Вах! Действительно, сделал менее агрессивную добавку к рыночному распределению, и график зависимости МОП от F для «лонг фьюч» изогнулся холмиком. Спасибо.
А можете, если не трудно, пояснить идею — как находить оптимальную позу (для распределения P) без геналгоритма?
Пока себе так представляю: задаю максимальное кол-во ячеек в позе (например, 5), максимальный объем в каждой ячейке (например, 10) и диапазон страйков (все/только центральные/только ликвидные и т.д.). В каждой ячейке может быть ничего/фьючерс/пут/колл. Объем в каждой ячейке от 1 до 10, мне кажется, достаточен чтобы обозначить любую пропорцию опционов. Случайным образом генерю начальную популяцию. Например:
1. [-],[-],[-],[-],[3*Fut]
2. [-],[-],[-],[5*Fut],[-10*90000C]
3. [-],[-],[-],[-6*90000С],[+10*95000C]
...
Расставляю оценки, оставляю какое-то кол-во лучших, скрещивание, мутация, добавка новой порции случайных поз и поехала эволюция.
Неужели можно как-то проще устроить перебор вариантов?
> А можете, если не трудно, пояснить идею —
> как находить оптимальную позу (для распределения P)
> без геналгоритма?
градиентным спуском из «нулевой позы», вот же как раз об этом — smart-lab.ru/blog/238736.php#comment3616586 и ещё следующий пост
или вы хотите именно решение в целых числах?
те посты несколько раз перечитал, но идею так и не уловил :(
Можете на небольшом примере пояснить — что такое градиентный спуск из «нулевой позы»?
1) рассматриваете только опционы колл (фьючерс = колл с нулевым страйком, а путы — это коллы минус фьючерс)
2) каждому коллу задаёте веса равные нулю. пусть это будет вектор w_0(strike), ожидаемая полезность такой позиции очевидно 0
3) для i-й итерации считаете производную ожидаемой полезности по каждому w_i(strike) — это и есть градиент, то есть рассчитываете вектор dMu/dw_i(strike) — как изменится ожидаемая полезность если веса w_i(strike) изменить на w_i(strike) + dw(strike)
4) приравниваете w_i+1(strike) = w_i(strike) — \lambda * dMu / dw(strike)
5) повторить с шага 3 пока не достигнете максимума ожидаемой полезности
в википедии неплохо написано ru.wikipedia.org/wiki/Градиентный_спуск
с небольшой поправкой, что в википедии ищут минимум, а требуется найти максимум
Спасибо! Правильно ли понял, что в векторе w_i(strike) координатой является страйк? Если, допустим у нас только два страйка: 1000 и 2000, то вектор w_i=(-5, 10, 0) — означает позу купленный стрэддл на страйке 1000? (-5*fut+10*call_1000)
Т.е. надо рассматривать позы, в которой потенциально могут быть коллы на все имеющиеся страйки + фьюч?
А точно при таком поиске будет находится глобальный максимум? Или возможно попасть только на какой-то локальный?
да, strike — координата, i — итерация
> Т.е. надо рассматривать позы, в которой
> потенциально могут быть коллы на все
> имеющиеся страйки + фьюч?
для фортса этого достаточно, т.к. опционы и маржируемые и на фьючерсы, то путы это функция от колов и фьюча, если бы были на акции и/или классические — то так уже было бы нельзя. можно и путы добавить, но сходимость может ухудшиться. если вы интегрируете численно — мб стоит исключить опционы сильно в деньгах / сильно вне денег — иначе они собирут большие ошибки (их платёжная функция не ноль где-то на хвостах распределений, а вы эти хвосты где-то всё равно обрубите)
> А точно при таком поиске будет находится
> глобальный максимум? Или возможно попасть
> только на какой-то локальный?
как-то я об этом не задумывался, мне кажется при довольно общих ограничениях типа не квазиарбитражности и P и Q, будет только один максимум, но надо перепроверить…
Спасибо. А если страйков, например, 30, то теоретически оптимальная поза может оказаться из 31 разных инструментов (30 коллов на разные страйки + фьюч)? Если — да, то ведь ее сложно будет открыть при реальной торговле?
Поделитесь, пожалуйста, результатом. Насколько понимаю, это можно в качестве w_0 взять не только нулевую позу, но и какую-нибудь случайную и убедиться что она приведет к той же оптимальной позе, что и нулевая.
А за сколько примерно итераций обычно алгоритм сходится? И сколько по времени (примерно) длятся расчеты?
> А если страйков, например, 30, то теоретически
> оптимальная поза может оказаться из 31 разных
> инструментов (30 коллов на разные страйки + фьюч)
> Если — да, то ведь ее сложно будет открыть
> при реальной торговле?
Почти наверное так и окажется — в оптимальную позицию войдут все инструменты, но это оптимальная позиция на рынке без спредов и издержек, что касается практики, если учитывать спреды при расчёте полезности, то многие инструменты отвалятся.
Поскольку ожидаемая полезность зависит только от функции выплат (обозначим её как PF) портфеля и распределения P, а функция выплат зависит от цен сделок, то на практике при поиске оптимальной позиции распределение Q не участвует:
U(F, T) = ln((S + PF(F, T)) / S)
PF(F, T) = sum(PF_C(F, T, K)) + sum(PF_P(F, T, K))
То есть функция выплат = сумма функций выплат для колов и для путов, суммирование по K — страйку. Фьючерс — воспринимаем как колл со страйком 0. На примере какого-нибудь отдельновзятого колла (для путов аналогично) имеем:
PF_C(F, T, K) = w_C(K) * max(F — K, 0) + EnterSaldo(w_C(K)),
где EnterSaldo(w_C(K)) — сальдо входа в позицию размером w_C(K) единиц инструмента. Например, купить 10 коллов со страйком K (w_C(K) = 10) в моменте можно 8 штук по 1250 и ещё 2 штуки по 1270, тогда:
EnterSaldo(10) = -8 * 1250 + -2 * 1270 = -12540
PF_C(F, T, K) = 10 * max(F — K, 0) — 12540
Таким образом влияние ликвидности на ожидаемую полезность учитывается через EnterSaldo(w)
Важно:
1) в EnterSaldo покупки берутся с минусом т.к. расход, продажи с плюсом, т.к. приход
2) в отличии от идеализированного случая, в котором можно было исключить из рассмотрения путы и ограничиться оптимизацией только портфеля колов, на практике следует рассматривать и колы и путы, поскольку их стаканы наполняются самостоятельно.
3) EnterSaldo(W) определена только в целых точках, и монотонно убывает, чтобы градиентный спуск продолжал работать, достаточно гладко доопределить эту функцию между целыми точками, сохранив при этом условие монотонности — это можно сделать массой методов, я ограничиваюсь сплайнами
>> но надо перепроверить…
> Поделитесь, пожалуйста, результатом.
сейчас большая загрузка… в ближайшее время не обещаю
> Насколько понимаю, это можно в качестве w_0 взять
> не только нулевую позу, но и какую-нибудь случайную
> и убедиться что она приведет к той же оптимальной
> позе, что и нулевая.
ну, кстати, тоже вариант, лучше наверное точек 10 случайных взять для надёжности ...
PS: а как Вы так сделали цитату с вертикальной чертой? это вручную через html или тут можно включить нормальный редактор комментариев? (у меня просто текстовое окно со скроллером, без какого-либо функционала)
Большое спасибо, что так подробно расписали!
Получается, набираете позу по рынку? Я то думал, если смогу реализовать поиск, то набирать позу котированием. Поэтому придется все-таки ограничивать возможное кол-во инструментов в позе (думаю, максимум 4-5).
А используете этот подход (поиск наилучшей позы на распределении P) для управления уже открытой позы?
Да, конечно, только если будет время и возможность. Очень уж интересно — один тут максимум или много локальных. Я то, наверное, через градиентный спуск сделать не смогу (не хватает матподготовки), и скорее всего буду делать просто в лоб, случайным перебором.
P.S. Цитату выделил вручную через вот такой тэг html.
Для котирования всё очень похоже, но сложнее, особенно если планируете держать несколько заявок одновременно, если делать правильно — нужно осреднять полезность не только по распределению P, но и дополнитеьлно по распределению вероятности исполнения котировочной заявки в зависимости от её цены и/или очереди перед ней, а так же учесть, что фьюч может оказаться не там где вы его видели, когда расчитывали ену котировки.
Допустим, Вы хотите котировать бид на какой-то бумаге, на ней имеется офер по цене MarketPriceAsk (далее = MP_a) и алгоритму набора позиций по рынку этот офер не интересен.
1) Предположим появляется новый офер по цене MP_a — MinTick * i на любой объём.
2а) Если этот офер стал интересен алгоритму набора позиций по рынку с оптимальным объёмом W, то собственно почему бы не поставить свой бид объёмом W на эту цену?
2б) Если этот виртуальный офер не стал интересен, то увеличиваем i и возвращаемся к шагу 1
> А используете этот подход (поиск наилучшей
> позы на распределении P) для управления уже
> открытой позы?
Да, конечно, оно «само» так и работает :) Если текущая позиция W', и ищется оптимальная позиция W'', то рассчитайте EnterSaldo по всем ранее заключённым сделкам приведшим к позиции W' + добавьте к нему сальдо открытия позиции dW = W''-W' по ценам стакана, максимизируйте ожидаемую полезность относительно W'', тогда вектор dW — это и будет управление позицией.
> Я то, наверное, через градиентный спуск сделать
> не смогу (не хватает матподготовки)
На самом деле не сложнее чем численное интегрирование. Пару слов о масштабе проблемы с производительностью:
— Градиентный спуск сойдётся наверное итераций за 20, в самой топорной реализации на каждой итерации надо посчитать полезность C*2 раза, где C кол-во страйков — итого примерно C*40 тяжеловесных операций;
— Перебор — если для инструментов рассматривать только варианты {лонг, нет позиции, шорт} это будет 3^C вычислений, при C = 6 перебор в 3 раза тяжелее и при никакой точности;
— У генетических алгоритмов с популяцией N, если мутирует K генов вероятность положительной мутации обратнопропорциональна C^K, на каждой итерации нужно посчитать полезность N*C^K раз, а точность решения будет порядка (1/N)^(1/C). Если популяцию взять 40, страйков 6, мутирующих генов 1, то уже после первой смены поколений генетика проигрывает градиенту по скорости, а точность примерно как у перебора с 3мя возможными состояниями {лонг, ноль, шорт}.
Спасибо, разница в производительности впечатляет! Есть над чем подумать...
Можете приоткрыть в общих чертах — как строите распределение P? Интуитивно или системно? ТА, ФА, прогоны на истории?
Что думаете про идею учитывать распределение ОИ по страйкам?
Не заметил Ваш новый большой пост, я тогда там вам и отвечу
UPD: пардон, это оказался этот же пост, но только внизу страницы, лучше отвечу здесь:
> Можете приоткрыть в общих чертах — как строите
> распределение P? Интуитивно или системно? ТА, ФА,
> прогоны на истории?
В посте про модель Хестнона, я начинал писать про приближение «сложного» распределения смешиванием нескольких «простых». Распределения P моделируется смесью двух логнормальных.
Сначала рассчитываются четыре момента Q. M1(Q) и M2(Q) отправляются в P без изменений. M3(P) и M4(P) моделируются регрессией от:
— предыдущих значения M3(P) и M4(P)
— текущих значения M3(Q) и M4(Q)
— текущей динамики M1(Q) и M2(Q)
Параметры компонентов смеси P находится при решении системы уравнений:
M1(P) = M1(Q)
M2(P) = M2(Q)
M3(P) = MODEL_OF_M3(...)
M4(P) = MODEL_OF_M4(...)
Регрессии для M3 и M4 оказались настолько устойчивыми, что я первый и последний раз их подбирал в 2012 году на данных за 2010 — 2012 года и больше ни разу не менял, мартовский и декабрьский форсмажоры переносятся более чем комфортно.
> Что думаете про идею учитывать распределение
> ОИ по страйкам?
Про ОИ думал, но не придумал. :) Вроде бы на предыдущей НОК был неплохой доклад на эту тему.
Получилось его посчитать или решили как-то обойтись без него?
Та идея так и осталась идеей. Тема с направленной торговлей показалась интереснее.
Спасибо, примерно понял.
Но ведь получается, что распределение P будет рискнейтральным (M1(P) = M1(Q) = текущ. БА)? Т.е. это не направленная торговля, а что-то вроде арбитража улыбки. В таком варианте ведь можно было просто теорцены рассчитать по распределению P, и бить по тем бид/аскам в стаканах, которые сильно отходят от них. И не нужен поиск оптимальной позы. Или я неправ, и что-то не учитываю?
А когда P становится равным Q — что делаете? Стараетесь закрыть позу или продолжаете управлять? Кстати, управление (через вектор dW) в таком случае будет эквивалентно дельта-вега хеджированию?
Не придумали — есть ли смысл в таком распределении, или не придумали — как строить плотность такого распределения?
Что-то не могу найти такой доклад в программе НОК-8
собственно это разговор вокруг да около критерия Келли, попробуйте первоисточник:
en.wikipedia.org/wiki/Kelly_criterion#Application_to_the_stock_market
--------
А как же нейронные сети, нечеткая логика? Вангоалгебра и Ностардамусиндикейшены?
На последней картинке у Вас изображен backspread, а не ratio.
Сам подход Ваш несколько оторван от реальной жизни, так как в большинстве случаев опционные позиции не удерживаются до экспирации, а трансформируются управлением.
Изыскания очень интересные. Но сама начальная посылка — «мы предполагаем рост и уверены в своем прогнозе на 5%. cоставляем смесь распределений» — очень модельная имхо. Качественный результат из нее можно получить, но вот количественный — какая поза лучше, какой страйк, размер профита — не уверен.
Для меня направленная торговля опционами сводится к минимизации потерь за счет веги/тэты/дельты. Достичь уровня (определяются по ТА) и соотв.профита — вот цель. И минимально потерять при таком же ходе в противоположную сторону. Горизонт 3-7 дней.
А какие комбинации для этого используете?
Продажа путов оказалась средненькой и проиграла лучшей по очкам в два раза.
Насчет «минимально потерять» — это не зигзаг ли имеется ввиду? Когда экспериментировал с изменением третьего момента у рыночного распределения, то иногда получал интересные профили PnL у зигзагов (на текущую дату, а не на экспу): в одну сторону профиль резко шел вверх, а в другую — довольно долго болтался у нуля, и только потом шел вниз.
Поэтому сейчас практикую голые путы/колы и стоп (в дельта-нейтраль) фьючем. Важно выбрать только момент входа (на эктремуме) и страйк.
Зигзаг — фигура интересная, но в силу особенностей улыбки, работает преимущественно на предполагаемый движ вверх, (иначе — центр проседает из-за волы).
Call Ratio Backspread» — в данной ситуации лучшая стратегия?
Если есть предположение, что БА на момент экспирации будет на 86000 то он будет убыточным
Во-вторых здесь походу не учитывается «тетта» — т.е. Call Ratio Backspread за 4 недели и за 3 дня по кривой доходности «live» будет разным и если цена застрянет на 86000, то будет убыток как раз не слабый!
Идея с поиском комбинаций не плохая — но на мой взгляд ех нужно по другому искать
Как? :)
Из Вашей задачи (как понял):
— поиск. оптимальной позы для входа (и/или упр. тек. позицией – т.е. та же задача но с ненулевым «нач. условиями») – это задача сравнения, т.е. задача перебора. Различные его методы(генетика, гр.спуск, деревья и т.п.) – это только попытки уйти от полного перебора и у каждого есть свои «+» и «-» и особенности/условия применения.
— оценка позы конечно может (или должна) проводиться несколькими параметрами, сам набор этих параметров проприетарен(имхо, отдельная тема – пропустим, чтобы не грузить топик). Но не факт, что их можно/нужно сводить к одной цифре, даже если этого как кажется «требует» к.л. метод поиска/перебора.
— тема поиска опт.количества, имхо, это отдельная от поиска лучшей позиции задача. И это уже совсем др. сказка… )))
Из практики:
— несколько лет назад решил эту задачку с исп. ген. алгоритма. Пришлось придумать как уйти от одного числа в фитнес-функции. Т.е. это только кажется (вернее, так написано в учебнике ))) ), что для ген. алгоритма, как впрочем и для град. спуска и для др. методов, нужно число для оценки.
— т.к. в опц. позе убытки(в том числе макс. могут быть больше тех, что на экспирацию) распределены по времени неравномерно, использовал платежную ф-цию на метки времени внутри прогнозируемого диапазона. Для этого пришлось использовать интегральную оценку позы по некой матрице/дереву девиаций цены БА и IV во времени. В этой оценке используется прогноз улыбок от времени и смещения БА + значения из этой матрицы.
— в качестве распределения можно использовать реальное ист. распределение + коррекции собственного вью (их можно «вытаскивать» из: от аналитики до индикаторов ТА и оценок опц. серий)
Вах, вот это круто, просто космический корабль! Я даже в мечтах на такое не замахивался. А используете в реале все это? Дает какое-нибудь преимущество по сравнению с подходом «на глазок»?
Вот тут готов поспорить. Сейчас попробую отдельный пост на эту тему написать. У меня получается, что это две неразрывные задачи.
Оч. интересно — чиркните, пжл, в скайп, когда напишите, а то редко читаю этот ресур. А когда будете писать, подумайте о их первичности/очередности по времени на практике. Т.к. на мой взгляд, это разговор о мани- и риск- менеджменте. Они, конечно, взаимосвязаны и в основе каждого могут даже лежать одни и те же величины. Но на практике одну из них нужно решить сначала, а вторую уже потом, например как при игре в рулетку: сначала нужно определиться со стоимостью фишек(SL) исходя из депозита,…, а потом уже управлять входом. Т.е. начинают, имхо, возникать между ними «направленные» связи.
Вот новый пост про оптимальный объем позы. Мне кажется, я там доказал, что поиск лучшей позы и оптимального объема — это одна общая задача.
Насчет используемого распределения, как смотрите на идею использовать не только рыночное/историческое/экспертное и т.д., но и распределение на основе ОИ на всех страйках? Ведь рыночное распределение — это то на что рынок сейчас готов поставить деньги, а распределение ОИ по страйкам — это то на что он уже поставил. Или в этом распределении уже нет никакой полезной инфы?