Модель Хестона и гэпы

Обнаружил несколько ошибок в своем прошлом исследовании Откуда возникает улыбка волатильности. В этом посте хотел бы их исправить (чтоб не стирать старый, там все-таки много интересного в комментариях). А также предложить на критику новую версию — откуда возникает улыбка и от каких факторов зависит.

Одна из ошибок того исследования была в предположении, что существует некая инерция в движениях цены БА: чем больше очередное приращение цены, тем больше вероятность что следующее приращение продолжится в том же направлении. Именно добавление этого эффекта в модель давало толстые хвосты и изгиб улыбки параболой. Но более внимательный анализ истории показал, что этого эффекта не наблюдается. Каким бы большим не было приращение — матожидание следующего будет ровно 0.

Но главной ошибкой было использование эмпирического распределения приращений для построения распределения цен на экспу. Понять что это ошибка, помогла всего одна фраза от
Арсена Яковлева (не ручаюсь за точность, но суть вроде такая):

Исторический ряд не повторится в будущем и лишь показывает свойства процесса движения цены.

Если поверить этому утверждению (а я сразу поверил), то конечно же неправильно брать приращения, которые были на историческом ряде, и только с помощью их пытаться построить все возможные случайные траектории цены. Более правильно было бы выявить некоторые закономерности на истории, оформить это в виде процесса, и потом уже с его помощью генерировать множество возможных траекторий цены.

Посему решил воспользоваться советом Андрея Агапова и поиграться с моделью Хестона. Реализовал в силу своего разумения, проверил на отдельных траекториях цены/волы, чтобы присутствовали основные факторы модели: отрицательная корреляция между ценой и волой, стремление мгновенной волы БА возвращаться к заданному среднему значению с заданной скоростью, волатильность у траектории волы была равна заданной величине (VolOfVol). Все это присутствовало в отдельных траекториях, но в итоговом распределении не получилось толстых хвостов, и улыбка была просто наклонной прямой:


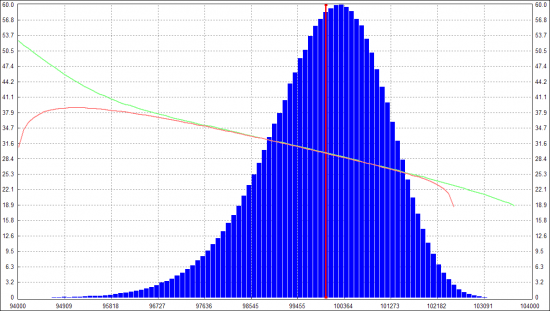
(зеленая линия — считаю по распределению цены колл и перевожу в IV по БШ; красная линия — тоже самое для путов; расхождение на хвостах — погрешность вычислений)

Кирилл Ильинский (во второй лекции), а также Unforgiven утверждали, что за изгиб улыбки в виде параболы отвечает VolOfVol. Но сколько не экспериментировал с этим параметром (даже делал его динамически меняющимся) — толстых хвостов не получалось и улыбка оставалась прямой.

Никита Масюков подсказал, что на изгиб улыбки может быть влияют прыжки цены. Попробовал смоделировать это так: с заданной вероятностью (небольшой) генерируется гэп, размер которого берется из нормального распределения, сигма которого в заданное кол-во раз больше сигмы, используемой во время обычного блуждания цены. Добавил это в модель и у полученного распределения появились толстые хвосты, правда изгиб у улыбки был очень слабенький. Тогда добавил такой эффект: если происходит гэп, то делаю взлет волы (не только для гэпа вниз, но и вверх тоже). И вот это уже хорошо загнуло улыбку в виде параболы:


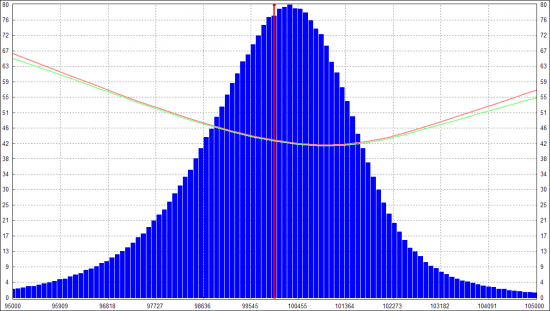
Тут бы успокоиться и просто порадоваться, что теперь примерно понятно откуда возникает улыбка. Но заметил проблему: IV на центре такой улыбки получался слишком большим. На картинке выше начальная вола БА = 30%, а IV на центре получилась 42-43%. В реале, насколько наблюдал, IV тоже выше чем HV, но все-таки не настолько. Если в модели снизить вероятность и размер гэпа, чтобы IV была только немного выше начальной волы, то улыбка становится почти плоской. Подсветить в чем проблема помогла HV-улыбка, на которую немного отвлекусь.

В какой-то момент захотелось проверить гипотезу, что улыбка IV показывает ожидание рынка — какая в среднем будет вола у БА, если цена придет на тот или иной страйк. Стал считать HV у каждой случайной траектории, и показывать это в виде облачка точек: по X финальная цена, куда пришла траектория на экспу, по Y — HV этой траектории. Вот что получилось для модели без гэпов:


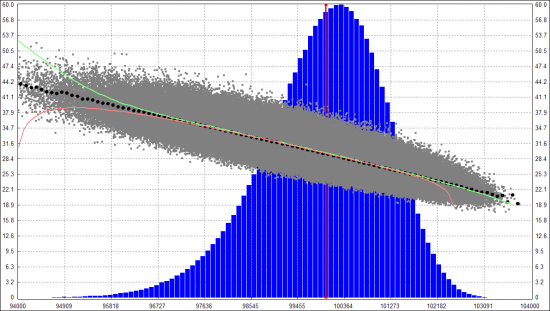
(черные кружочки — среднее HV на соответствующем участке, решил назвать это HV-улыбкой)

Видно что IV и HV улыбки очень хорошо совпали. Но вот если добавить гэпы (и на время убрать отрицательную корреляцию между БА и волой), то картина получается такая:



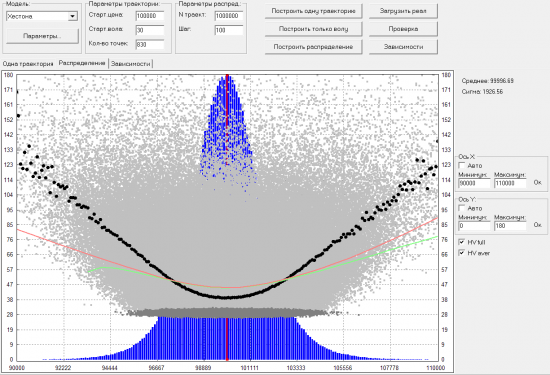
Здесь уже IV и HV плохо совпадают. Но главное видно почему поднимается улыбка IV при моделировании гэпов. В самом низу проглядывает горизонтальное облачко (точки темно-серого цвета), на уровне 30% (именно такая была стартовая вола у всех траекторий). Точки из этого облачка соответствуют траекториям в которых не было гэпа. А все точки выше него (светло-серого цвета) соответствуют траекториям, в которых был хотя бы один гэп. Получается что траектории  с гэпами, которые возвращались к стартовому значению цены, имеют такую же высокую волу, как и те, которые унесло далеко в сторону. Из общих соображений, решил что это неправильно. Интуитивно хочется, чтобы облако HV траекторий с гэпами, было не равномерно рассеяно, а группировалось вокруг улыбки. Что-то вроде такой картинки:



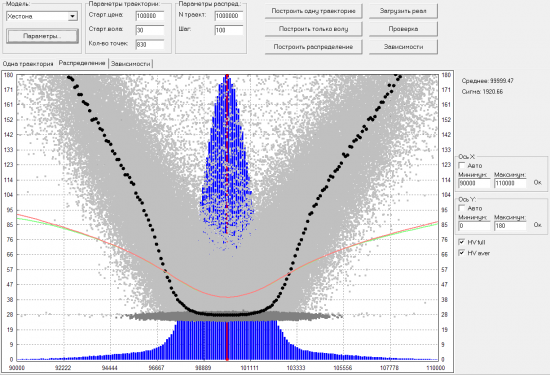
Но получил ее не совсем честным путем. А хотелось бы добавить что-то в модель, чтобы такая группировка получалась по-честному. Что-нибудь типа такого: если гэп в сторону от стартового значения цены, то идет рост волы, а если потом случается гэп в обратную сторону, то не увеличивать волу еще больше, а наоборот возвращать ее к стартовым значениям. Правда, пока не понимаю как это формализовать.

В общем, хотелось бы посоветоваться — в правильном ли направлении двигаюсь или уже занесло куда-то не туда. Допустимо ли добавлять в модель гэпы и всплески волы после них, или загиба улыбки в виде параболы можно было добиться одним VolOfVol и нужно искать ошибку в своей реализации модели Хестона?