26 декабря 2012, 14:11
Роботы: алгоритмы целочисленных и распределённых вычислений.
При создании робота, как и любой задаче по программированию,
есть стадия формирования решения в виде логической блок-схемы,
и есть стадия технического воплощения элементов.
Качество робота, кроме чёткости исполнения алгоритма,
в значительной степени определяется скоростью расчёта
актуальных рынку команд.
Для начала сделаем общую оценку. Самая хлопотная,
ресурсоёмкая и «бесполезная» часть робота — взаимодействие
с «хомосапиенсом»: графики, формы, таблицы и прочие
штуки никакой полезности собственно алгоритму не дают,
поэтому по-возможности хорошо бы от них избавиться.
Далее, компьютер в своей основе — это инструмент обработки
целых чисел 0 и 1. Все прочие он с определённой точностью
и скоростью выражает при помощи этих двух. Поэтому данные,
которые будет обрабатывать алгоритм, следует изначально
выразить в формат, удобный компьютеру.
В частности рассмотрим цену инструмента. Терминалы
транслируют её, как число с плавающей десятичной точкой.
Однако, если реально посмотреть любой инструмент,
для примера возьмём акции Сбербанка, то видно,
что диапазон возможных значений, выраженных в пунктах
минимального изменения цены составляет 1-20000,
где 1 — это 1 цена в копейку, а 20000 — цена в 200,00 рублей.
Конечно в долгосрочной перспективе цена Сбера может уйти
в область чисел ВТБ или Транснефти, но это для срока в 1 год
в данный момент событие из разряда нереальных.
Из этого можно сделать вывод, что для хранения данных
о цене Сбера внутри алгоритма нам хватит 2-х байтов
или числа целочисленного типа Int16. А расчётные значения
элементов ТА (средние и пр.) вполне поместятся в Int32.
Если по каким-то причинам график всё таки хочется увидеть,
то это лишь задача нарисовать шкалы в «цифрах хомосапиенса».
Теперь о распределённых вычислениях.
Если принятие решения основано на значениях элементов ТА:
средних, стохастиков и пр., то чем больше расчётный период,
тем больший объём данных необходимо обработать для каждого
бара. Если захотим в секундный таймфрейм запихнуть
расчёт средней цены за квартал (т.е. за период в 10 млн.
баров приментительно к данному таймфрейму), то очень
возможно задача станет не решаемой в реальном времени
или...
В общем виде формула средней величины это:
Pср = (P(i-n) + P(i-n+1) +… + P(i-1)) / n, где
n — период или число баров;
i — текущий бар.
Запишем формулу для следующего бара (i+1):
Pср = (P(i+1-n) + P(i+1-n+1) +… + P(i+1-1)) / n или
Pср = (P(i-n+1) + P(i-n+2) +… + P(i)) / n
Посмотрев на обе суммы видно, что они различаются лишь
2-мя слагаемыми:
— в первой сумме есть P(i-n), которого нет во второй;
— во второй сумме есть P(i), которого нет в первой.
Или иначе говоря к сумме на каждом баре прибывает
новый элемент и убывает самый дальний. Следовательно,
если на каждом баре мы будем считать сумму
накопительным итогом, то для расчёта средней нам
достаточно из суммы для текущего бара вычесть
сумму для (i-n)-ного бара и поделить на n,
и мы получим среднюю. Для любого числа баров
вычисление средней будет происходить практически
с одинаковой скоростью независимо от мощности компьютера.
Ещё для примера возьмём стохастик.
Ситуация где-то очень похожая — нам для расчёт нужно найти
максимум и минимум цены за n-ное количество баров.
Соответственно цены для каждого бара необходимо выполнить
сортировку по всему диапазону, сравнив каждый с каждым,
поскольку нельзя сказать как изменило ситуацию
в новом баре «выпадание» самого дальнего для предыдущего
и приход нового.
В решении этой задачи используем двойную индексацию.
Для примера будем искать минимум.
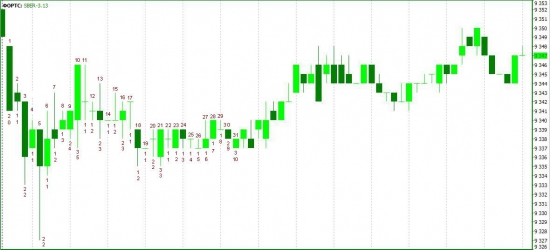
На рисунке 1-вый индекс (верхняя цифра снизу свечи)
показывает минимум текущего бара для скольки
предыдущих баров, включая самого себя, является таковым.
2-рой индекс (нижняя цифра снизу свечи) указывает
на сколько отстоит текущий бар от последнего,
для которого выполнилось условие 1-вый индекс больше K-1,
где К — критерий периодичности (в примере равен 2).
Т.е. мы отмечаем те бары, минимум которых является таковым
для двух и более предыдущих, включая самого себя.
Тогда на каждом баре нам достаточно пересчитать
оба индекса. А алгоритм поиска минмума будет «прыгать»
по отмеченным выбирая минимальный между ними.
В примере нам нужно сделать сортировку лишь для 9 баров,
из 31. Если мы хотим найти минимум за 31 бар.
И дополнительно для каждого из тех баров, которые
дяльше нижнего индекса дальнего отмеченного, но попавшие
в требуемый диапазон.
Если мы будем повышать К, то можем быстро пробежать
любой период.
Если сделать ещё и несколько ступеней (для перебора
остающихся самых дальних), то можно в реальном времени
брать стохастик любого периода, работая в секундном
тайм-фрейме.
Удачи в написании роботов и поиске нетривиальных
решений в Новом 2013 году!
есть стадия формирования решения в виде логической блок-схемы,
и есть стадия технического воплощения элементов.
Качество робота, кроме чёткости исполнения алгоритма,
в значительной степени определяется скоростью расчёта
актуальных рынку команд.
Для начала сделаем общую оценку. Самая хлопотная,
ресурсоёмкая и «бесполезная» часть робота — взаимодействие
с «хомосапиенсом»: графики, формы, таблицы и прочие
штуки никакой полезности собственно алгоритму не дают,
поэтому по-возможности хорошо бы от них избавиться.
Далее, компьютер в своей основе — это инструмент обработки
целых чисел 0 и 1. Все прочие он с определённой точностью
и скоростью выражает при помощи этих двух. Поэтому данные,
которые будет обрабатывать алгоритм, следует изначально
выразить в формат, удобный компьютеру.
В частности рассмотрим цену инструмента. Терминалы
транслируют её, как число с плавающей десятичной точкой.
Однако, если реально посмотреть любой инструмент,
для примера возьмём акции Сбербанка, то видно,
что диапазон возможных значений, выраженных в пунктах
минимального изменения цены составляет 1-20000,
где 1 — это 1 цена в копейку, а 20000 — цена в 200,00 рублей.
Конечно в долгосрочной перспективе цена Сбера может уйти
в область чисел ВТБ или Транснефти, но это для срока в 1 год
в данный момент событие из разряда нереальных.
Из этого можно сделать вывод, что для хранения данных
о цене Сбера внутри алгоритма нам хватит 2-х байтов
или числа целочисленного типа Int16. А расчётные значения
элементов ТА (средние и пр.) вполне поместятся в Int32.
Если по каким-то причинам график всё таки хочется увидеть,
то это лишь задача нарисовать шкалы в «цифрах хомосапиенса».
Теперь о распределённых вычислениях.
Если принятие решения основано на значениях элементов ТА:
средних, стохастиков и пр., то чем больше расчётный период,
тем больший объём данных необходимо обработать для каждого
бара. Если захотим в секундный таймфрейм запихнуть
расчёт средней цены за квартал (т.е. за период в 10 млн.
баров приментительно к данному таймфрейму), то очень
возможно задача станет не решаемой в реальном времени
или...
В общем виде формула средней величины это:
Pср = (P(i-n) + P(i-n+1) +… + P(i-1)) / n, где
n — период или число баров;
i — текущий бар.
Запишем формулу для следующего бара (i+1):
Pср = (P(i+1-n) + P(i+1-n+1) +… + P(i+1-1)) / n или
Pср = (P(i-n+1) + P(i-n+2) +… + P(i)) / n
Посмотрев на обе суммы видно, что они различаются лишь
2-мя слагаемыми:
— в первой сумме есть P(i-n), которого нет во второй;
— во второй сумме есть P(i), которого нет в первой.
Или иначе говоря к сумме на каждом баре прибывает
новый элемент и убывает самый дальний. Следовательно,
если на каждом баре мы будем считать сумму
накопительным итогом, то для расчёта средней нам
достаточно из суммы для текущего бара вычесть
сумму для (i-n)-ного бара и поделить на n,
и мы получим среднюю. Для любого числа баров
вычисление средней будет происходить практически
с одинаковой скоростью независимо от мощности компьютера.
Ещё для примера возьмём стохастик.
Ситуация где-то очень похожая — нам для расчёт нужно найти
максимум и минимум цены за n-ное количество баров.
Соответственно цены для каждого бара необходимо выполнить
сортировку по всему диапазону, сравнив каждый с каждым,
поскольку нельзя сказать как изменило ситуацию
в новом баре «выпадание» самого дальнего для предыдущего
и приход нового.
В решении этой задачи используем двойную индексацию.
Для примера будем искать минимум.

На рисунке 1-вый индекс (верхняя цифра снизу свечи)
показывает минимум текущего бара для скольки
предыдущих баров, включая самого себя, является таковым.
2-рой индекс (нижняя цифра снизу свечи) указывает
на сколько отстоит текущий бар от последнего,
для которого выполнилось условие 1-вый индекс больше K-1,
где К — критерий периодичности (в примере равен 2).
Т.е. мы отмечаем те бары, минимум которых является таковым
для двух и более предыдущих, включая самого себя.
Тогда на каждом баре нам достаточно пересчитать
оба индекса. А алгоритм поиска минмума будет «прыгать»
по отмеченным выбирая минимальный между ними.
В примере нам нужно сделать сортировку лишь для 9 баров,
из 31. Если мы хотим найти минимум за 31 бар.
И дополнительно для каждого из тех баров, которые
дяльше нижнего индекса дальнего отмеченного, но попавшие
в требуемый диапазон.
Если мы будем повышать К, то можем быстро пробежать
любой период.
Если сделать ещё и несколько ступеней (для перебора
остающихся самых дальних), то можно в реальном времени
брать стохастик любого периода, работая в секундном
тайм-фрейме.
Удачи в написании роботов и поиске нетривиальных
решений в Новом 2013 году!
Читайте на SMART-LAB:

Вышел эфир RENI для Bazar
Благодарим платформу Bazar за приглашение на разговор! Хотя, видео вышло с заголовком «Шокирующая правда о рынке страхования в 2026 году | Ренессанс Страхование», единственное, чем мы хотели...
11:59
Российский рынок остается в узком диапазоне
Торги 20 февраля на российских фондовых площадках начались ростом. К 12:30 мск индексы Мосбиржи и РТС прибавляли по 0,26% каждый, достигая 2780 и 1143 пунктов соответственно, а индекс голубых фишек...
13:35

Софтлайн полностью погасил пятый выпуск облигаций
Друзья, рады сообщить, что сегодня мы полностью погасили выпуск облигаций серии 002Р-01 на сумму 6 млрд рублей. Все обязательства перед держателями облигаций SOFL выполнены в полном объеме и в...
13:44

Россети Центр и Приволжье. Отчет об исполнении инвестпрограммы за Q4 2025г. Дивидендная база по РСБУ удивляет.
Компания Россети Центр и Приволжье (сокр. ЦиП) опубликовала отчет об исполнении инвестпрограммы за Q4 2025г., где показаны финансовые показатели компании по РСБУ в 4 квартале (ну и понятно...
18.02.2026










Просто повышать К нельзя. Если К=2 нам достаточно сравнить
минимум текущего бара с предыдущим, чтобы пересчитать оба
индекса. Если мы лишь повысим К, то даже при 3 алгоритм
может работать с ошибками. Для К=3 минимум текущего бара
нужно сравнивать с предыдущим и перед предыдущим,
соответственно с ростом К, растёт и количество баров,
значения которых нужно сравнить для пересчёта индексов.
Поэтому возможно эффективней использовать К=2, но добавлять
ещё пары индексов для сортировки уже среди помеченных.
Тогда максимальное количество обрабатываемых баров будет
убывать со скоростью 2 в степени С, где С-число индексных
пар. Ну и разумеется нужно сохранять номер бара предыдущего
минимума, поскольку возожно и для текущего попадает
в диапазон и тогда вообще ничего сортировать не придётся.
индекса