07 ноября 2012, 15:12
Кто сказал что золотого сечения нет? TRNF
Сегодня были закрыты последние лонги по Транснефти на уровне 65000.
Далее приведу пару графиков с занимательной математикой.
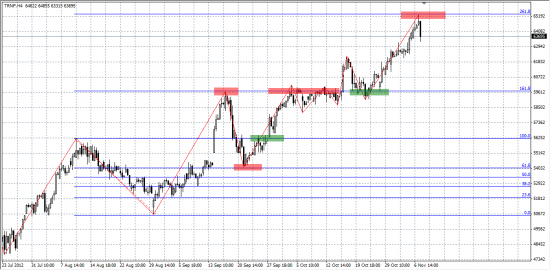
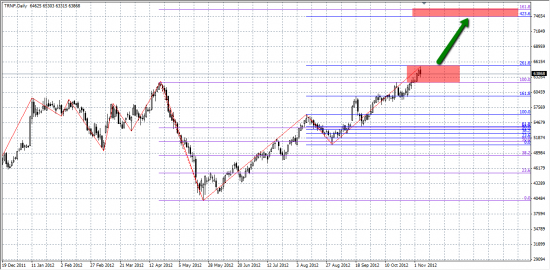
Ожидаю консолидацию на уровне 65000-62000. После этого возобновление среднесрочного восходящего движения с целевым уровнем 75000
P.S.
Леона́рдо Пиза́нский (лат. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи (Fibonacci); о происхождении этого псевдонима имеются разные версии. По одной из них, его отец Гильермо имел прозвище Боначчи («Благонамеренный»), а сам Леонардо прозывался filius Bonacci («сын Благонамеренного»). По другой, Fibonacci происходит от фразы Figlio Buono Nato Ci, что в переводе с итальянского означает «хороший сын родился».
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама (таких как ал-Хорезми и Абу Камил); по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.
Исследовал последовательность чисел, совокупность которых позже была названа в его честь числами Фибоначчи.
Вот первые несколько членов этой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 и т.д. Каждый следующий член последовательности Фибоначчи, начиная со второго, получается сложением двух предыдущих: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5 и т.д. Обозначим n-й член последовательности как tn (n ≥ 1). Последовательность чисел tn обладает рядом замечательных свойств. Так, если вычислять последовательно отношение каждого члена к предыдущему, то получаемое отношение будет сходиться к иррациональному числу α:
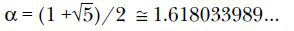
известному как значение золотого сечения.
Далее приведу пару графиков с занимательной математикой.


Ожидаю консолидацию на уровне 65000-62000. После этого возобновление среднесрочного восходящего движения с целевым уровнем 75000
P.S.
Леона́рдо Пиза́нский (лат. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи (Fibonacci); о происхождении этого псевдонима имеются разные версии. По одной из них, его отец Гильермо имел прозвище Боначчи («Благонамеренный»), а сам Леонардо прозывался filius Bonacci («сын Благонамеренного»). По другой, Fibonacci происходит от фразы Figlio Buono Nato Ci, что в переводе с итальянского означает «хороший сын родился».
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама (таких как ал-Хорезми и Абу Камил); по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.
Исследовал последовательность чисел, совокупность которых позже была названа в его честь числами Фибоначчи.
Вот первые несколько членов этой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 и т.д. Каждый следующий член последовательности Фибоначчи, начиная со второго, получается сложением двух предыдущих: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5 и т.д. Обозначим n-й член последовательности как tn (n ≥ 1). Последовательность чисел tn обладает рядом замечательных свойств. Так, если вычислять последовательно отношение каждого члена к предыдущему, то получаемое отношение будет сходиться к иррациональному числу α:
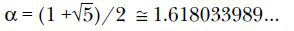
известному как значение золотого сечения.
19 Комментариев
 Алексей (rwsmart)07 ноября 2012, 15:17плюсую ++1
Алексей (rwsmart)07 ноября 2012, 15:17плюсую ++1 Алексей07 ноября 2012, 15:34что по ВТБ думаешь, как то странно она себя ведёт.Вообще победа Обамы это позитив для банковского сектора.0
Алексей07 ноября 2012, 15:34что по ВТБ думаешь, как то странно она себя ведёт.Вообще победа Обамы это позитив для банковского сектора.0 r1msy07 ноября 2012, 15:40Да что там говорить, если в мире столько всего устроено по золотому сечению, то уж цена то тем более0
r1msy07 ноября 2012, 15:40Да что там говорить, если в мире столько всего устроено по золотому сечению, то уж цена то тем более0 cruss1u507 ноября 2012, 15:54Да нету его… можно любой сечение придумать и ламерам показвать на СБ что оно работает+3
cruss1u507 ноября 2012, 15:54Да нету его… можно любой сечение придумать и ламерам показвать на СБ что оно работает+3
Читайте на SMART-LAB:
18 лет в коммерческой недвижимости: Accent делится опытом
Accent Capital — это инвестиционная компания с фокусом на коммерческой недвижимости. Мы на рынке с 2007 года и специализируемся на управлении активами, которые соответствуют институциональным...
15:53
🚀 МТС Банк: про бизнес и портфель
Market Power задал несколько вопросов представителю банка. Публикуем его ответы. ➡️ Отчет компании разобрали здесь ❓ Вопрос МР: Каковы причины снижения непроцентного дохода в 2025 году?...
15:11











